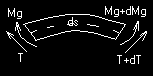
ZASADY STATYKI

0≤ M ≤

T QR=Nf

Prawo superpozycj i: m a = P 1 + P 2 + ... + P n przyśpieszenie punktu

Przyrost krętu ciała materialnego względem dowolnego bieguna

1. Zasada równoległoboku – dwie siły przyłożone do jednego punktu

materialnego na który działają siły P 1... P n równe jest sumie wywołamy działaniem siły chwilowej jest równy momentowi jej

możemy zastąpić jedną siłą wypadkową, która jest przekątną

Tarcie pasów o koła

geometrycznej przyśpieszeń, które miałby ten punkt gdyby każda siła

impulsu względem przyjętego bieguna.

równoległoboku zbudowanego na tych wektorach

αµ

S=S

działała z osobna

1e

; α- kąt opasania; S,S1 – siła naciągu pasa

2. Dwie siły przyłożone do ciała sztywnego są w równowadze gdy

PRĘT

Bezwładnościowy układ odniesienia – układ względem którego

Uderzenie proste – przypadek w którym prędkości punktów

działają wzdłuż jednej prostej i mają te same wartości, ale przeciwne

Pręt – bryła której jeden wymiar wyraźnie dominuje nad pozostałymi.

obowiązują prawa dynamiki Newtona. Każdy układ odniesienia

stykających się ciał leżą na jednej prostej normalnej do powierzchni

zwroty. Układ taki nazywamy zerowym.

Pręt powstaje w wyniku przesuwania figury płaskiej A wzdłuż

poruszający się względem układu bezwładnościowego jednostajnym

obu ciał.

3. Działanie układu sił nie ulegnie zmianie, gdy do układu tego

krzywej k, tak że figura pozostaje zawsze prostopadła do krzywej k, a

ruchem postępowym jest także układem bezwładnościowym.

Uderzenie środkowe – jeżeli normalna uderzeniowa przechodzi przez

dodamy układ wzajemnie równoważących się sił.

jej środek ciężkości zawsze znajduje się na krzywej k. Figurę płaską

Zasada krętu – pochodna wektora krętu względem czasu t jest równa

środek mas uderzających o siebie ciał.

4. Zasada zesztywnienia działanie układu sił nie ulegnie zmianie przez

nazywamy przekrojem normalnym pręta a krzywą k – osią pręta.

momentowi siły działającej na punkt materialny obliczanego

zesztywnienie ciała na które działają te siły.

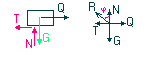
T- siła poprzeczna

względem tego samego punktu co kręt.

Hipoteza Poissona – Impuls s ’’ odpowiadający drugiemu okresowi 5. Każdemu działaniu towarzyszy równe co do wartości o przeciwnym

N – siła normalna

d K 0/dt = M 0

uderzenia (prędkości są sobie równe siła wzajemnego oddziaływania

zwrocie i leżące na tej samej prostej przeciwdziałanie.

M

Zasada zachowania krętu – jeżeli w pewnym okresie czasu moment

maleje do 0) związany jest z impulsem s’ odpowiadającemu

s – moment skręcający

6. Zasada oswobodzenia z więzów – każde ciało nieswobodne można

M

siły działającej na punkt materialny jest stale równy 0, wówczas kręt

pierwszemu okresowi uderzenia (rozpoczynającym się w momencie

g – moment gnący

oswobodzić z więzów zastępując je reakcjami. Wówczas można

jest stały.

zetknięcia, aż do momentu w którym prędkości na skutek

rozpatrywać takie ciało jako swobodne znajdujące się pod działaniem

Siłą normalną w przekroju aa nazywamy sumę rzutów wszystkich sił

Zasada względności mechaniki klasycznej – Za pomocą żadnych

odkształceniom nie zrównają się) związkiem:

sił sztywnych i biernych.

znajdujących się po jednej stronie przekroju na kierunek normalny do

zjawisk

mechanicznych

nie

możemy

wykazać

istnienia

przekroju (dodatnia jeżeli powoduje rozciąganie).

prostoliniowego

jednostajnego

ruchu

postępowego

układu

s’’ = k * s’ k – współczynnik restytucji wyznaczmy na podstawie

Momentem siły P względem punktu 0 nazywamy iloczyn wektorowy

Siłą poprzeczną w przekroju aa nazywamy sumę wszystkich sił

odniesienia.

doświadczeń

tej siły przez promień – wektor łączący 0 z dowolnym punktem na

znajdujących się po jednej stronie przekroju (względem jego środka

k=1 dla ciał doskonale sprężystych

linii działania tej siły.

ciężkości) na kierunek prostopadły do osi przekroju.

PRACA, MOC, ENERGIA

Momentem siły P względem osi l nazywamy rzut wektora momentu

Moment zginający przekroju aa nazywamy rzut wektora momentu

Więzy – czynniki ograniczające ruch ciała

siły obliczonego względem dowolnego punktu na osi l na kierunek tej

będącego sumą momentów wszystkich sił znajdujących się po jednej

Praca mechaniczna – praca siły stałej na drodze prostoliniowej,

Reakcje – siły oddziaływania więzów

siły.

stronie przekroju na kierunek styczny do przekroju (dodatni gdy

kierunek działania siły pokrywa się z drogą.

Klasyfikacja więzów :

powoduje wygięcie wypukłe w dół).

Przesunięcie elementarne – nieskończenie mały wektor d s o Geometryczne - równanie więzów zawiera tylko współrzędne punktów

Para sił to układ sił równoległych o tych samych wartościach

Tw.

Schwedlera.

pochodna

momentu

gnącego

względem

wielkości równej różniczce łuku drogi.

Kinematyczne - równanie więzów zależy od prędkości

liczbowych lecz zwrotach przeciwnych.

współrzędnej pokrywającej się z osią pręta jest równa sile poprzecznej

d s = dx i +dy j + dz k

Reonomicze, niestacjonarne - zależy od czasu

Własności

d M

Elementarną praca siły zmiennej P na elementarnym przesunięciu d s

Skleronomiczne, stacjonarne - niezależne od czasu

g/ ds. =T; d2M.g/dx2=dT/dx=-q; q – gęstość obciążenia

-moment pary sił nie zależy od wyboru bieguna względem którego

KRATOWNICE

nazywamy iloczyn skalarny tej siły przez przesunięcie.

Auholonomiczne – zależne od prędkości

wyznaczamy i jest wartością stałą.

Pręt prosty nieobciążony na długości i zakończony przegubami to pręt

δL = P• ds ; δL =Pxdx + Pydy + Pzdz ; LAB = ∫AB(δL) = ∫AB(Pxdx +

Gładkie, idealne – więzy w których nie występują reakcje sztywne

-każdą parę sił działającą w dowolnej płaszczyźnie możemy zastąpić

przegubowy

Pydy + Pzdz)

Obustronne φj(x, y, z ... xn, yn, zn) = 0

inną parą sił działającą w tej samej płaszczyźnie o momencie równym

ϕ

Kratownica to układ pr

B

ętów przegubowych połączonych ze sobą

dla toru kołowego: δL = M0dϕ ; LAB = ∫ϕA (M0dϕ)

Jednostronne φj(x, y, z ... xn, yn, zn) =< 0, >= 0

momentowi pierwotnemu.

przegubami. Kratownica jest płaska jeśli pręty i obciążenia leżą w

Moc – praca odniesiona do jednostki czasu

Holonomiczne – niezależne od prędkości

-pary sił działające w jednej płaszczyźnie możemy zastąpić jedną parą

jednej płaszczyźnie

N = dW/dt = P*(d r/dt) = P• v

sił o momencie równym sumie momentów poszczególnych par sił

Warunek konieczny na to aby kratownica była geometrycznie

dla ruchu obrotowego: N = (M

ω

Współrzędne uogólnione – odpowiednio dobrane niezależne

0dϕ)/dt = M0

-pary sił działające w różnych płaszczyznach możemy zastąpić parą o

niezmienna – P=2W-3; P- pręty; W – węzły (przeguby)

Sprawność – stosunek pracy użytecznej do pracy włożonej

parametry pozwalające określić położenie nieswobodnego układu

momencie równym sumie geometrycznej momentów sił.

Metody wyznaczania sił w prętach kratownicy

L

materialnego. Ilość współrzędnych uogólnionych jest równa liczbie

c = Lµ + Lst - straty

analogiczne

η = (L

swobody układu.

µ/Lc) < 1

REDUKCJA DOWOLNEGO UKŁADU SIŁ

1)równoważenia węzłów – wycinamy węzły w kratownicach i

Zasada równoważności pracy i energii kinetycznej: Skończony

Przesunięcia możliwe – zgodne z więzami

M

n

o=Σa=1 M a – moment główny układu sił

piszemy warunki równowagi dla każdego z osobna

przyrost energii kinetycznej układu mechanicznego ciał materialnych

S=Σ

n

k=1 P k – wektor główny układu sił

z położenia o konfiguracji elementów A do położenia o konfiguracji

Przesunięcia przygotowane (wirtualne) – przesunięcia proporcjonalne

M 01= M 0- r× s - wzór Bosma (moment siły S względem bieguna O

elementów B jest równy sumie prac całkowitych układów sił

do prędkości możliwych (zgodnych z więzami).

gdzie r = OO 1)

zewnętrznych i zewnętrznych na tym przemieszczeniu

Praca przygotowana – elementarna praca siły P na przygotowanym

M •

2

2

przesunięciu jej punktu przyłożenia

O1 S= M O S=k=const Iloczyn momentu głównego względem mVB /2 – mVA /2 = LAB ; EkB – EkA = LAB

dowolnego punktu ciała i wektora głównego układu jest równy

Przyrost E

Zasada Lagrange’a-d’Alemberta (prac przygotowanych) – WKW

k w czasie od t1 do t2 jest równy pracy wykonanej przez siłę

iloczynowi mom. gł. układu względem bieguna redukcji O i jest stały

działającą na punkt materialny w tym samym czasie.

równowagi układu materialnego jest, aby suma prac przygotowanych

= k.

z wszystkich sił czynnych i reakcji więzów przy dowolnym

S jest pierwszym niezmiennikiem układu sił.

P O L A P O T E N C J A L N E

przesunięciu przygotowanym była równa zero.

n

k – parametr układu jest drugim niezmiennikiem układu sił.

2)przecięć Rittera – piszemy 3 warunki momentów (tylko 1

Pole wektorowe - ograniczony obszar w którym każdemu punktowi

Σ

δ

i=1 Pi ri = 0

niewiadoma)

przyporządkowano wektor.

Siły uogólnione - siły wykonujące pracę elementarną na

Skrętnik – wynik redukcji dla którego wektor momentu głównego M.O

wykreślne

Pole wirowe niezachowawcze, niepotencjalne – pola, w których

odpowiadającej współrzędnej uogólnionej

jest wektorem równoległym do wektora głównego S

1)Cremana

L

praca zależy od kształtu toru.

δL = Σ

δ

k=1 Qk qk Qj = d/dt( ∂Ek/∂qj) - ∂Ek/∂qj 2)Cluman

L

Siła uogólniona jest równa zmianie w czasie pochodnej E

AB = ∫AB(Pxdx + Pydy + Pzdz)

k układu

Oś centralna układu – prosta równoległa do wektora głównego S, na

Pole potencjalne – to pole sił, w którym praca nie zależy od drogi względem odpowiedniej prędkości uogólnionej, pomniejszonej o

której leżą wszystkie bieguny redukcji, względem których układ

KINEMATYKA

przejścia, lecz tylko od położenia punktu początkowego i końcowego.

pochodną Ek względem współrzędnej uogólnionej.

redukuje się do skrętnika.

Prędkości i przyspieszenia

Praca po linii zamkniętej w polu potencjalnym wynosi 0. Jeżeli

istnieje funkcja pola F(x,y,z), z której różniczka: dF = (∂F/∂x)dx +

Równanie Lagrange’a I rodzaju:

Równanie parametryczne osi centralnej

f

(∂F/∂y)dy + (∂F/∂z)dz , to pole nazywamy potencjalnym.

R

λ

ix = Σj=1

j*( ∂Fj/∂xj) = mix’’i - xi

(M

f

x-(ySz-zSy))/Sx= (My-(zSx-xSz))/Sy= (Mz-(xSy-ySx))/Sz

Potencjał pola sił – taka skalowana funkcja położenia V(x,y,z), której

R

λ

iy = Σj=1

j*( ∂Fj/∂yj) = miy’’i - yi

f

pochodne cząstkowe podług odpowiednich kierunków są równe

R

λ

iz = Σj=1

j*( ∂Fj/∂zj) = miz’’i - zi

TABLICA REDUKCJI

składowym siły pola w tych kierunkach wziętych ze znakiem „-”.

S

M.O

K

Wynik

Miejsce geometryczne punktów, w których funkcja V przyjmuje

Równanie Lagrange’a II rodzaju:

S≠0

M. ≠

jednakową wartość, nazywamy powierzchnią izoskalarną, lub

Q

O 0

K≠0

Skrętnik lub 2 siły równoległe

j = d/dt( ∂Ek/∂qj) - ∂Ek/∂qj j=1,2,,....,k

S≠0

M. ≠

ekwipotencjalną. Aby pole było potencjalne to: rot P = 0 ; rot P =

O 0

K=0

Wypadkowa

(∂P

Twierdzenie Vorginiona – moment siły wypadkowej dowolnego

S≠0

M.

z/∂y - ∂Py/∂z)i + (∂Px/∂z - ∂Pz/∂x)j + (∂Py/∂x - ∂Px/∂y)k

O=0

K=0

Wypadkowa

Zasada zachowania energii mechanicznej – w polu potencjalnym

układu sił względem dowolnego punktu równy jest sumie momentów

S=0

M. ≠

O 0

K=0

Para sił

V= d r/dt=d r/ds. * ds./dt=ds./dt * τ

suma energii kinetycznych i potencjalnej jest wartością stałą.

wszystkich sił składowych tego układu względem tego punktu.

S=0

M.O=0

K=0

Równowaga układu sił

| V|=ds./dt V=V*τ

E

Kr

kA + VA = EkB + VB

ęt k= r× p; k= r ×m V

a=d V/dt=d/dt(V*τ)=dV/dt * τ + V*dτ/dt

Wnioski dotyczące pól potencjalnych:

SZCZEGÓLNE UKŁADY SIŁ

a= d 2 s/dt2 * τ + V2/r * n

1)Potencjał jest to skalarna funkcja położenia, określona jako: gradV

Zbieżny układ sił – układ sił których linie działania przecinają się w

= - P

jednym punkcie. Jeżeli wszystkie siły układu zbieżnego leżą w jednej

Stopnie swobody – liczba niezale

2)Potencjał istnieje w polu, w którym: rot P = 0

żnych parametrów potrzebnych do

płaszczyźnie układ taki nazywamy płaskim zbieżnym układem sił.

określenia położenia ciała sztywnego w przestrzeni.

3)W polu potencjalnym praca elementarna jest równa różniczce

Każdy płaski układ sił można zredukować do wypadkowej

Ciało swobodne (nie poddawane działaniu więzów posiada 6 stopni

zupełnej potencjału ze znakiem „-” δL = -dV

M

n

0-(xΣi=1 Piy-Pix)=0 – równanie prostej działania wypadkowej

swobody) n = 6 – w . Funkcje określające położenie ciała nazywamy

4)Praca całkowita w polu potencjalnym jest równa różnicy

równaniami ruchu ciała sztywnego (ich ilość równa jest ilości stopni

potencjałów i nie zależy od kształtu drogi

Warunki równowagi płaskiego układu sił M.O=0 , S=0

swobody)

5)Praca całkowita w polu potencjalnym po torze zamkniętym jest

Ruch kulisty – taki ruch ciała sztywnego, podczas którego jeden jego

równa 0

Układ sił równoległych – układ sił których linie działania są do siebie

punkt pozostaje nieruchomy (środek ruchu kulistego). W ruchu

6)Siły pola są prostopadłe do powierzchni izoskalarnych

równoległe. Układ sił da się zredukować do wypadkowej k=0 lub pary

kulistym torami punktu ciała są krzywe, które leżą na powierzchniach

7)Siły pola są zwrócone od powierzchni wyższego potencjału do

sił gdy S=0. Środek sił równoległych to punkt zaczepienia ich

kul o promieniach równych odległościom tych punktów od punktu

powierzchni niższego potencjału.

wypadkowej

nieruchomego.

Pole stałe – pole, w którym siła jest stała co do kierunku, zwrotu i Środek sił równoległych – określa się jako współrzędne xs, ys, zs

v = ω × r ; a = ε × r

wartości.

xs=(ΣxiPi)/ ΣPi; ys==(ΣyiPi)/ ΣPi; zs=(ΣziPi)/ ΣPi;

Ruch obrotowy – ruch wokół prostej łączącej dwa nieruchome

Pole centralne (środkowe) – wielkość siły w dowolnym punkcie pola

zależy tylko od odległości od jego środka.

Moment statyczny punktu materialnego względem dowolnej

Moment bezwładności punktu materialnego względem płaszczyzny,

płaszczyzny to iloczyn masy tego punktu i jego odległości od

osi lub bieguna nazywamy iloczyn masy punktu przez kwadrat

płaszczyzny.

odległości tego punktu od danej płaszczyzny osi, czy bieguna.

Środek ciężkości to punkt w którym skupiona masa układu ma

Promień bezwładności – taka odległość od płaszczyzny, osi lub

względem dowolnej płaszczyzny lub osi taki sam moment statyczny

bieguna, której kwadrat pomnożony przez masę układu da nam jego

jak cały układ materialny

moment bezwładności.

Masa zredukowana – masa, która pomnożona przez kwadrat

TWIERDZENIA DOTYCZĄCE ŚRODKA MASY:

odległości od osi, płaszczyzny lub bieguna da nam moment

1)środek masy układu płaskiego leży w płaszczyźnie tego układu

bezwładności.

2)środek masy linii prostej leży na tej linii

punkty ciała sztywnego. Prostą nazywamy osią obrotu.

Momentem zboczenia (dewiacji) układu punktów materialnych

3)środek masy dwóch punktów materialnych leży na prostej łączącej

ω = dϕ/dt ; | aτ| = ε*r = [d2ϕ/dt2]*r | a n| = ω2*r ; v = ω × r

względem dwóch wzajemnie prostopadłych płaszczyzn nazywamy

te punkty i dzieli ją na odcinki o długościach odwrotnie

sumę iloczynów mas tych punktów przez odległości od tych

proporcjonalnych do ich mas.

Ruch postępowy – ruch, w którym dowolna prosta sztywno związana

płaszczyzn.

4)Środek masy układu mającego środek symetrii leży w tym środku.

z poruszającym się ciałem pozostaje stale równoległa do położenia,

I

m

m

m

xy = Σi=1 (mixiyi) ; Iyz = Σi=1 (miyizi) ; Izx = Σi=1 (mizixi) ; Ixy =

Jeżeli układ ma 2 lub więcej osi symetrii to środek leży w punkcie

jakie zajmowała w dowolnie obranej chwili czasu t, na przykład w

∫m(xy)dm ...

przecięcia się tych osi

chwili początkowej.

Twierdzenie Steinera – moment bezwładności względem dowolnej

5)Rzut środka ciężkości figury płaskiej na dowolną płaszczyznę jest

Ruch płaski – ruch, w którym wszystkie punkty ciała poruszają się w

osi jest równy momentowi osi równoległej i przechodzącej przez

środkiem ciężkości rzutu tej figury na dowolną płaszczyznę.

płaszczyznach równoległych

do

pewnej

płaszczyzny zwanej

środek masy układu powiększonemu o iloczyn masy całkowitej i

6)Moment statyczny względem osi lub płaszczyzny przechodzącej

płaszczyzną kierującą.

kwadratu odległości między tymi osiami. I = I0 + md2

przez środek ciężkości jest zawsze równy 0.

V B = V A + ω × AB ; V B = V A + V BA ; a B = a A + a BA ; a B = a A + a sBA Główne momenty bezwładności – pierwiastki równania sekularnego

7)Moment statyczny nie zmieni się jeżeli zamiast części układu

+ a nBA

I1>I2>I3 , gdzie I1 = Imax, I3 = Imin

wprowadzimy punkt materialny o masie równej masie danej części

Chwilowy środek prędkości w ruchu płaskim – jeżeli chwilowa

leżący w środku ciężkości tej części masy.

prędkość kątowa jest niezerowa to musi istnieć taki punkt, którego

1)Każda oś symetrii jest osią główną.

prędkość jest równa zero.

2)Każda prosta prostopadła do płaszczyzny symetrii jest też osią

Chwilowy środek przyśpieszeń – w ruchu płaskim jeżeli ω i ε nie są

główną.

jednocześnie równe zero istnieje punkt, którego przyśpieszenie jest

3)Każda prosta, na której leżą środki mas warstw elementarnych

równe zero.

otrzymywanych przez podział ciała płaszczyznami prostopadłymi do

Ruch unoszenia – ruch układu ruchomego względem nieruchomego

tej prostej też jest osią główną.

układu odniesienia.

4)Momenty dewiacji względem głównych osi bezwładności są równe

Ruch względny – ruch punktu względem układu ruchomego.

zero.

Ruch bezwzględny – ruch punktu względem układu nieruchomego.

5)Jeżeli główne osie bezwładności przechodzą przez środek masy

Prędkość bezwzględna – jest równa wektorowej sumie prędkości

układu to nazywamy je centralnymi.

względnej i unoszenia V b = V w + V u

Ruch i własności dynamiczne środka masy

Przyśpieszenie bezwzględne – jest wektorową sumą przyśpieszenia

6)Pęd ogólny układu punktów materialnych równa się pędowi masy

względnego, unoszenia i Coriolisa

całkowitej układu umieszczonej w środku masy.

a b = a w + a u + a c

7)Środek masy układu punktów materialnych porusza się tak jakby

gdzie a w – przyśpieszenie punktu względem ruchomego układu

była w nim skupiona całkowita masa układu poddana działaniu sumy

TARCIE KINETYCZNE

odniesienia

wszystkich sił.

a u – przyśpieszenie punktu układu ruchomego pokrywającego się z 8)Pochodna pędu głównego układu punktów materialnych równa się

danym punktem

sumie wszystkich sił działających na układ.

Q

a

Twierdzenie Kóniga – energia kinetyczna ciała sztywnego równa się

GR=µG; TMAX=µT; 0≤Q≤ QGR; 0≤T≤TGR

c = 2 ω×Vw przyśp. Coriolisa

sumie energii kinetycznej ruchu postępowego całej masy skupionej w

tgϕ

D Y N A M I K A

środku masy oraz energii kinetycznej ruchu obrotowego ciała

gr= TGR/N=µN/N=µ ; ϕgr=arctgµ ; 0≤ϕ≤ϕGR

Zasada pędu – pochodna wektora pędu względem czasu t jest równa

sztywnego dookoła osi przechodzącej przez środek masy.

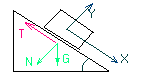
Tarcie na równi pochyłej

sile działającej na punkt materialny

E

ω2

k = mu2/2 + Ik

F = d p/dt

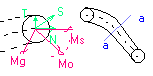
Reakcje dynamiczne łożysk osi obrotu

Zasada zachowania pędu – jeżeli na ciało nie działają żadne siły lub

RAz = (-ω2/l)Iyz ; RAx = (-ω2/l)Ixy ; ROx = (ω2/l)Ixy - ω2xsm ; ROz =

Suma P

działające pozostają w równowadze ( P = 0) to pęd ciała jest stały p =

(ω2/l)I

X=0 Gsinα-T=0

yz - ω2zsm

Suma P

const.

Y=0 N-Gcosα=0

Prawa dynamiki Newtona

T

Jeżeli reakcje dynamiczne są niezerowe układ jest dynamicznie nie

MAX=µT; TMAX= Gsinαmax; tgαmax=µ

α

1)Jeżeli na punkt materialny w pewnym okresie czasu nie działają

wyważony. Reakcje dynamiczne będą zerowe jeżeli oś obrotu będzie

max=arctgµ warunek samohamowalności równi

żadne siły lub siły działające wzajemnie się równoważą, to punkt

jedną z głównych centralnych osi bezwładności wirującego ciała.

pozostaje w spoczynku, lub porusza się ruchem jednostajnym po linii

Żyroskop – ciało symetryczne obracające się dookoła materialnej osi

prostej.

symetrii, przy czym jeden z punktów osi jest nieruchomy.

2)Przyśpieszenie

punktu

materialnego

ma

wartość

wprost

Precesja – ruch, jaki powstaje jeżeli ciało wprowadzimy w obrót z

proporcjonalną do wartości działającej siły i ma jej kierunek i zwrot F

prędkością kątową wokół materialnej osi symetrii, a równocześnie osi

= m a

symetrii nadamy ruch obrotowy dookoła osi w ustalonej przestrzeni.

3)Jeżeli na punkt materialny A działa punkt materialny B to również

punkt materialny B działa na punkt materialny A siłą równą co do

TEORIA UDERZENIOWA

wartości i kierunku o zwrocie przeciwnym. Siły te leżą na prostej

Siły chwilowe – siły które działając na ciało materialne w ciągu łączącej oba te punkty.

bardzo krótkiego czasu osiągają bardzo duże wartości w porównaniu z

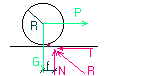
Tarcie przy toczeniu

Prawo

powszechnego

ciążenia

–

dwa

punkty

materialne

siłami np. ciężkości.

oddziaływują na siebie siłami ≈ (m1m2)/r2 ; | P| = k*(m1m2)/r2

QR=NT f- współ. tarcia przy toczeniu

Siła bezwładności. Zasada d’Alamberta: P + B = 0 Siły działające τ

Impuls - ∫ Pdt = s

0

na ciało są w równowadze z siłą bezwładności.

NfMax=MT moment tarcia przy toczeniu