ZASADY STATYKI

1. Zasada równoległoboku - dwie siły przyłożone do jednego punktu możemy zastąpić jedną siłą wypadkową, która jest przekątną równoległoboku zbudowanego na tych wektorach

2. Dwie siły przyłożone do ciała sztywnego są w równowadze gdy działają wzdłuż jednej prostej i mają te same wartości, ale przeciwne zwroty. Układ taki nazywamy zerowym.

3. Działanie układu sił nie ulegnie zmianie, gdy do układu tego dodamy układ wzajemnie równoważących się sił.

4. Zasada zesztywnienia działanie układu sił nie ulegnie zmianie przez zesztywnienie ciała na które działają te siły.

5. Każdemu działaniu towarzyszy równe co do wartości o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.

6. Zasada oswobodzenia z więzów - każde ciało nieswobodne można oswobodzić z więzów zastępując je reakcjami. Wówczas można rozpatrywać takie ciało jako swobodne znajdujące się pod działaniem sił sztywnych i biernych.

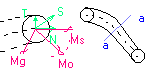
Momentem siły P względem punktu 0 nazywamy iloczyn wektorowy tej siły przez promień - wektor łączący 0 z dowolnym punktem na linii działania tej siły.

Momentem siły P względem osi l nawywamy moment rzutu siły F na płaszczyznę prostopadłą do osi z względem pkt 0 w którym os przebija plaszczyzne.

Para sił to układ sił równoległych o tych samych wartościach liczbowych lecz zwrotach przeciwnych.

Własności

-moment pary sił nie zależy od wyboru bieguna względem którego wyznaczamy i jest wartością stałą.

-każdą parę sił działającą w dowolnej płaszczyźnie możemy zastąpić inną parą sił działającą w tej samej płaszczyźnie o momencie równym momentowi pierwotnemu.

-pary sił działające w jednej płaszczyźnie możemy zastąpić jedną parą sił o momencie równym sumie momentów poszczególnych par sił

-pary sił działające w różnych płaszczyznach możemy zastąpić parą o momencie równym sumie geometrycznej momentów sił.

REDUKCJA DOWOLNEGO UKŁADU SIŁ

M_o=Σ_a=1ⁿM_a - moment główny układu sił

S=Σ_k=1ⁿP_k - wektor główny układu sił

M₀₁=M_0­-r×s - wzór Bosma (moment siły S względem bieguna O gdzie r = OO₁)

M_O1•S= M_OS=k=const Iloczyn momentu głównego względem dowolnego punktu ciała i wektora głównego układu jest równy iloczynowi mom. gł. układu względem bieguna redukcji O i jest stały = k.

S jest pierwszym niezmiennikiem układu sił.

k - parametr układu jest drugim niezmiennikiem układu sił.

Skrętnik - wynik redukcji dla którego wektor momentu głównego M._O jest wektorem równoległym do wektora głównego S

Oś centralna układu - prosta równoległa do wektora głównego S, na której leżą wszystkie bieguny redukcji, względem których układ redukuje się do skrętnika.

Równanie parametryczne osi centralnej

(M_x-(yS_z-zS­y))/S_x= (M_y-(zS_x-xS_z))/S_y= (M_z-(xS_y-yS­_x))/S_z

TABLICA REDUKCJI

S	M.O	K	Wynik
S≠0	M.O≠0	K≠0	Skrętnik lub 2 siły równoległe
S≠0	M.O≠0	K=0	Wypadkowa
S≠0	M.O=0	K=0	Wypadkowa
S=0	M.O≠0	K=0	Para sił
S=0	M.O=0	K=0	Równowaga układu sił

SZCZEGÓLNE UKŁADY SIŁ

Zbieżny układ sił - układ sił których linie działania przecinają się w jednym punkcie. Jeżeli wszystkie siły układu zbieżnego leżą w jednej płaszczyźnie układ taki nazywamy płaskim zbieżnym układem sił.

Każdy płaski układ sił można zredukować do wypadkowej

M₀-(xΣ_i=1ⁿP_iy-P_ix)=0 - równanie prostej działania wypadkowej

Warunki równowagi płaskiego układu sił M._O=0 , S=0

Układ sił równoległych - układ sił których linie działania są do siebie równoległe. Układ sił da się zredukować do wypadkowej k=0 lub pary sił gdy S=0. Środek sił równoległych to punkt zaczepienia ich wypadkowej

Środek sił równoległych - określa się jako współrzędne x_s, y_s, z_s x_s=(Σx_iP_i)/ ΣP_i; y_s==(Σy_iP_i)/ ΣP_i; z_s=(Σz_iP_i)/ ΣP_i;

Moment statyczny punktu materialnego względem dowolnej płaszczyzny to iloczyn masy tego punktu i jego odległości od płaszczyzny.

Środek ciężkości to punkt w którym skupiona masa układu ma względem dowolnej płaszczyzny lub osi taki sam moment statyczny jak cały układ materialny

TWIERDZENIA DOTYCZĄCE ŚRODKA MASY:

1)środek masy układu płaskiego leży w płaszczyźnie tego układu

2)środek masy linii prostej leży na tej linii

3)środek masy dwóch punktów materialnych leży na prostej łączącej te punkty i dzieli ją na odcinki o długościach odwrotnie proporcjonalnych do ich mas.

4)Środek masy układu mającego środek symetrii leży w tym środku. Jeżeli układ ma 2 lub więcej osi symetrii to środek leży w punkcie przecięcia się tych osi

5)Rzut środka ciężkości figury płaskiej na dowolną płaszczyznę jest środkiem ciężkości rzutu tej figury na dowolną płaszczyznę.

6)Moment statyczny względem osi lub płaszczyzny przechodzącej przez środek ciężkości jest zawsze równy 0.

7)Moment statyczny nie zmieni się jeżeli zamiast części układu wprowadzimy punkt materialny o masie równej masie danej części leżący w środku ciężkości tej części masy.

TARCIE KINETYCZNE

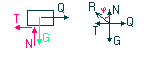
Q_GR=μG; T_MAX=μT; 0≤Q≤ Q_GR; 0≤T≤T_GR

tgϕ_gr= T_GR/N=μN/N=μ ; ϕ_gr=arctgμ ; 0≤ϕ≤ϕ_GR

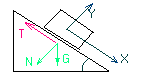
Tarcie na równi pochyłej

Suma P_X=0 Gsinα-T=0

Suma P_Y=0 N-Gcosα=0

T_MAX=μT; T_MAX= Gsinα_max; tgα_max=μ

α_max=arctgμ warunek samohamowalności równi

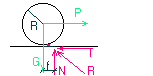
Tarcie przy toczeniu

QR=NT f- współ. tarcia przy toczeniu

Nf_Max=M_T moment tarcia przy toczeniu

0≤ M_T≤QR=Nf

Tarcie pasów o koła

S=S₁e^αμ; α- kąt opasania; S,S₁ - siła naciągu pasa

PRĘT

Pręt - bryła której jeden wymiar wyraźnie dominuje nad pozostałymi. Pręt powstaje w wyniku przesuwania figury płaskiej A wzdłuż krzywej k, tak że figura pozostaje zawsze prostopadła do krzywej k, a jej środek ciężkości zawsze znajduje się na krzywej k. Figurę płaską nazywamy przekrojem normalnym pręta a krzywą k - osią pręta.

T- siła poprzeczna

N - siła normalna

M_s - moment skręcający

M_g - moment gnący

Siłą normalną w przekroju aa nazywamy sumę rzutów wszystkich sił znajdujących się po jednej stronie przekroju na kierunek normalny do przekroju (dodatnia jeżeli powoduje rozciąganie).

Siłą poprzeczną w przekroju aa nazywamy sumę wszystkich sił znajdujących się po jednej stronie przekroju (względem jego środka ciężkości) na kierunek prostopadły do osi przekroju.

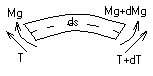
Moment zginający przekroju aa nazywamy rzut wektora momentu będącego sumą momentów wszystkich sił znajdujących się po jednej stronie przekroju na kierunek styczny do przekroju (dodatni gdy powoduje wygięcie wypukłe w dół).

Tw. Schwedlera. pochodna momentu gnącego względem współrzędnej pokrywającej się z osią pręta jest równa sile poprzecznej dM_g/ds.=T; d²M._g/dx²=dT/dx=-q; q - gęstość obciążenia

KRATOWNICE

Pręt prosty nieobciążony na długości i zakończony przegubami to pręt przegubowy

Kratownica to układ prętów przegubowych połączonych ze sobą przegubami. Kratownica jest płaska jeśli pręty i obciążenia leżą w jednej płaszczyźnie

Warunek konieczny na to aby kratownica była geometrycznie niezmienna - P=2W-3; P- pręty; W - węzły (przeguby)

Metody wyznaczania sił w prętach kratownicy

analogiczne

1)równoważenia węzłów - wycinamy węzły w kratownicach i piszemy warunki równowagi dla każdego z osobna

2)przecięć Rittera - piszemy 3 warunki momentów (tylko 1 niewiadoma)

wykreślne

1)Cremana

2)Cluman

KINEMATYKA

Prędkości i przyspieszenia

V=dr/dt=dr/ds. * ds./dt=ds./dt * τ

|V|=ds./dt V=V*τ

a=dV/dt=d/dt(V*τ)=dV/dt * τ + V*dτ/dt

a= d²s/dt² * τ + V²/r * n

Stopnie swobody - liczba niezależnych parametrów potrzebnych do określenia położenia ciała sztywnego w przestrzeni.

Ciało swobodne (nie poddawane działaniu więzów posiada 6 stopni swobody) n = 6 - w . Funkcje określające położenie ciała nazywamy równaniami ruchu ciała sztywnego (ich ilość równa jest ilości stopni swobody)

Ruch kulisty - taki ruch ciała sztywnego, podczas którego jeden jego punkt pozostaje nieruchomy (środek ruchu kulistego). W ruchu kulistym torami punktu ciała są krzywe, które leżą na powierzchniach kul o promieniach równych odległościom tych punktów od punktu nieruchomego.

v = ω × r ; a = ε × r

Ruch obrotowy - ruch wokół prostej łączącej dwa nieruchome punkty ciała sztywnego. Prostą nazywamy osią obrotu.

ω = dϕ/dt ; |a_τ| = ε*r = [d²ϕ/dt²]*r |a_n| = ω²*r ; v = ω × r

Ruch postępowy - ruch, w którym dowolna prosta sztywno związana z poruszającym się ciałem pozostaje stale równoległa do położenia, jakie zajmowała w dowolnie obranej chwili czasu t, na przykład w chwili początkowej.

Ruch płaski - ruch, w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej płaszczyzny zwanej płaszczyzną kierującą.

V_B = V_A + ω × AB ; V_B = V_A + V_BA ; a_B = a_A + a_BA ; a_B = a_A + a^s_BA + aⁿ_BA

Chwilowy środek prędkości w ruchu płaskim - jeżeli chwilowa prędkość kątowa jest niezerowa to musi istnieć taki punkt, którego prędkość jest równa zero.

Chwilowy środek przyśpieszeń - w ruchu płaskim jeżeli ω i ε nie są jednocześnie równe zero istnieje punkt, którego przyśpieszenie jest równe zero.

Ruch unoszenia - ruch układu ruchomego względem nieruchomego układu odniesienia.

Ruch względny - ruch punktu względem układu ruchomego.

Ruch bezwzględny - ruch punktu względem układu nieruchomego.

Prędkość bezwzględna - jest równa wektorowej sumie prędkości względnej i unoszenia V_b = V_w + V_u

Przyśpieszenie bezwzględne - jest wektorową sumą przyśpieszenia względnego, unoszenia i Coriolisa

a_b = a_w + a_u + a_c

gdzie a_w - przyśpieszenie punktu względem ruchomego układu odniesienia

a_u - przyśpieszenie punktu układu ruchomego pokrywającego się z danym punktem

a_c = 2ω×V_w przyśp. Coriolisa

---