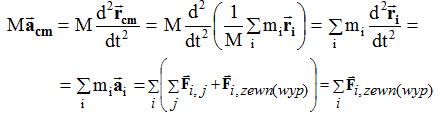1. Omówić równowagę trwałą, chwiejną i obojętną dla punktu materialnego.

2. Wyprowadzić zasadę zachowania pędu dla układu punktów materialnych.

3. Zderzenia elastyczne i nieelastyczne. Przykłady.

4. Ruch ciał o zmiennej masie. Równanie Ciołkowskiego.

5. Definicja wektora położenia środka masy, wektora prędkości, przyśpieszenia i pędu środka masy.

6. Pokazać, że w inercjalnym układzie odniesienia całkowita zmiana pędu układu cząstek jest proporcjonalna do wypadkowej sił zewnętrznych działających na ten układ.

7. Pokazać, że w inercjalnym układzie odniesienia pęd układu cząstek jest równy pędowi środka masy.

8. Pokazać, że w inercjalnym układzie odniesienia przyspieszenie środka masy układu cząstek jest proporcjonalne do wypadkowej sił zewnętrznych.

9. Definicja momentu siły i momentu pędu dla punktu materialnego.

10. Wyprowadzić II zasadę dynamiki dla ruchu obrotowego punktu materialnego r

(τ = r

Iα )

1. Jeżeli środek ciężkości znajduje się na linii pionowej przechodzącej przez punkt zawieszenia i środek ciężkości znajduje się w najniższym możliwym położeniu to ciała jest w równowadze trwałej.

Jeżeli w najbliższym otoczeniu środek ciężkości przy odchodzeniu od położenia równowagi nie zmienia się to mamy równowagę obojętną.

Jeżeli maleje – równowaga chwiejna.

2. Zasada zachowania pędu:

Jeśli układ cząstek jest izolowany, to całkowity pęd układu nie zmienia się.

p (t) = const.

Wyprowadzenie:

Sposób 1:

F12 = - F21

F12 = dp1 / dt F21 = dp2 / dt

dp1 / dt = - dp2 / dt dp1 / dt + dp2 / dt = 0 d/dt(p1 + p2) = dpc / dt = 0

pc = const.

Sposób 2 :

dp / dt = d/dt ∑

∑

i pi = ∑i dpi / dt = ∑i Fwyp, i = ∑i

i≠j Fij = 0

3. Zderzenia:

Vi – prędkość początkowa pi – pęd początkowy

Vf – prędkość końcowa pf – pęd końcowy

a) Jeśli cząstki przed lub po zderzeniu mają te same prędkości to zderzenie jest nieelastyczne:

m1V1i + m2V2i = (m1 + m2)Vf ,dla wektorów V

m1V1i + m2V2i = (m1 + m2)Vf ,skalarnie

pi = pf

b) Jeśli całkowita energia nie zmienia się to zderzenie jest elastyczne: m1V1i + m2V2i = m1V1f + m2V2f ,dla wektorów V

m

2

2

2

2

1V1i / 2 + m2V2i / 2= m1V1f / 2 + m2V2f / 2

m1V1i - m2V2i = m1V1f + m2V2f ,skalarnie

4.

V + dV

V

m

m-dmx

u V - u

V – prędkość rakiety w pewnym inercjalnym układzie odniesienia w chwili t u – prędkość gazów względem rakiety

(V – u) – prędkość gazów w inercjalnym układzie odniesienia

V + Dv – prędkość rakiety w chwili (t + dt)

m – dms – dms elementarna masa porcji wyrzucanych gazów

p1 = p2

mV = (m - dms)(V + dV) + dms(V – u)

mV = mV - dmsV + mdv - dmsdV + dmsV - dmsu ,dmsdV → 0

mdV = dmsu | :dt

mdV / dt = udms / dt

ma = udms / dt

Fciągu = u * dms/dt

Równanie Ciołkowsksiego (wyprowadzenie) :

mdV = dmsu

mdv = -dmu | * 1/mu

dV/u = -dm/m | ∫

1/u ∫dV = -∫ dm/m

V/u + c1 = -ln m + c2 ,c = c1 + c2

* V/u = -ln m + c

Niech dla t=0 v=v0 m=m0

1/u*V0 = -ln m0 + c

c = V0/u + ln m0 → *

u/V = -ln m + ln m0 + V0/u

V = V0 + u*ln m0/m

5.

a) Wektor położenia środka masy:

r

1

r

m r

cm =

∑

i i

M

i

b) Wektor prędkości środka masy:

1

V

m V

cm =

∑

i

i

M

i

c) Wektor przyspieszenia środka masy:

1

a

m a

cm =

∑

i

i

M i

d) Wektor pędu środka masy:

1

p

m p

cm =

∑ i i

M i

6. Wyprowadzenie:

݀

݉௨ݎŚெ = ݉ଵݎଵ + ݉ଶݎଶ + ⋯ + ݉௡ݎ௡ | ݀ݐ

݀

݉௨ݒŚெ = ݉ଵݒଵ + ݉ଶݒଶ + ⋯ + ݉௡ݒ௡ |݀ݐ

݀݌௨

݀ݐ = ݉ଵܽଵ + ݉ଶܽଶ + ⋯ + ݉௡ܽ௡

݀݌௨

݀ݐ = ෍ ܨ௜,௭௘௪௡ę௧௥௭.௪௬௣.

௜

7. Wyprowadzenie:

݀ݎ

݀ 1 ௡

1 ௡

݀ݎ

1 ௡

1 ௡

1

ܸ

Śெ݉

௜

Śெ =

݀ݐ = ݀ݐ ൭ܯ ෍ ݉௜ݎ௜൱ = ܯ ෍ ݉௜ ݀ݐ = ܯ ෍ ݉௜ݒ௜ = ܯ ෍ ݌௜ = ܯ ݌

௜ୀଵ

௜ୀଵ

௜ୀଵ

௜ୀଵ

݌Śெ = ܯܸŚெ

8. Wyprowadzenie:

r

r

Macm = ∑ F i, zewn( wyp) i

9. Moment siły dla punktu materialnego określamy wzorem:

r

r

r

τ ≡ r ×F

i definiujemy jako jako iloczyn wektorowy pomiędzy wektorami położenia i siły.

Kierunek momentu siły określami zgodnie z regułą śruby prawoskrętnej, a wartość momentu siły obliczamy ze wzoru M=rFsinα.

Moment pędu dla punktu materialnego określamy wzorem:

L ≡ r × p

I definiujemy jako iloczyn wektorowy pomiędzy wektorami położenia i pędu. Wektor L i jego wartość zależy od położenia punktu.

10. Wyprowadzenie:

݀ܮ ݀(ܫϣ)

݀ϣ

߬ = ݀ݐ = ݀ݔ = ܫ ݀ݐ = ܫߙ