dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III Zero-Beta Capital Asset Pricing Model

Aby otrzymać stan równowagi rynku należy zagregować pojedyncze wybory inwestorów.

Założenia:

- nienasyconość i awersja do ryzyka jak w teorii Markowitza

- kwadratowa funkcja użyteczności

- rozkład normalny stóp zwrotu

Oznacza to że:

•

2

inwestor maksymalizuje oczekiwaną stopę R minimalizując jej wariancję σ

• przyrost stopy zwrotu δR jakiego inwestor oczekuje w zamian za podjęcie dodatkowej jednostki ryzyka

2

δσ zwiększa się wraz ze wzrostem poziomu

2

ryzyka σ

1

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III

• W przestrzeni wartość oczekiwana stopy zwrotu / wariancja stopy zwrotu preferencje inwestorów przedstawiają krzywe obojętności.

• Punkt styczności krzywych obojętności do granicy efektywnej to portfel optymalny dla inwestora.

2

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III Załóżmy, iż inwestor i zgłasza popyt na portfel wi leżący na granicy efektywnej.

Niech ω i oznacza wskaźnik mierzący udział inwestora i w globalnym popycie na walory w gospodarce w:

w = ∑ω w

i

i

i

Kombinacja liniowa portfeli ze zbioru minimalnego ryzyka jest także portfelem leżącym w zbiorze minimalnego ryzyka

=>

portfel w jest także portfelem minimalnego ryzyka 3

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III Zachodzi także własność: R

> R

wi

g

Zatem:





R = ∑ω R > ∑ω R =  ∑ω R



= R

w

i

w

i

g

i

g

g

i





i

i

i

=> portfel w leży na granicy efektywnej

=> w ≠ g.

4

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III Strona podażowa dana jest w postaci portfela m, zwanego portfelem rynkowym ( market portfolio).

Założenia dotyczące portfela rynkowego:

• Popyt

na

każdy

walor

w

portfelu

rynkowym

jest

dodatni (przeważa pozycja długa inwestorów na walorze)

• Udział waloru w portfelu rynkowym jest proporcjonalny do udziału wszystkich uczestników gospodarki w tym waloru (skalowalność)

• Portfel rynkowy składa się z aktywów n=1,…, N które podlegają wycenie rynkowej na giełdach zatem portfel rynkowy jest obserwowalny 5

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III W stanie równowagi popyt równa jest podażowi m = w

=> obserwowalny portfel rynkowy musi leżeć na granicy efektywnej Na podstawie własności portfeli efektywnych: oczekiwana stopa zwrotu z portfela jest liniową funkcją kowariancji (współczynnika beta) z portfelem rynkowym

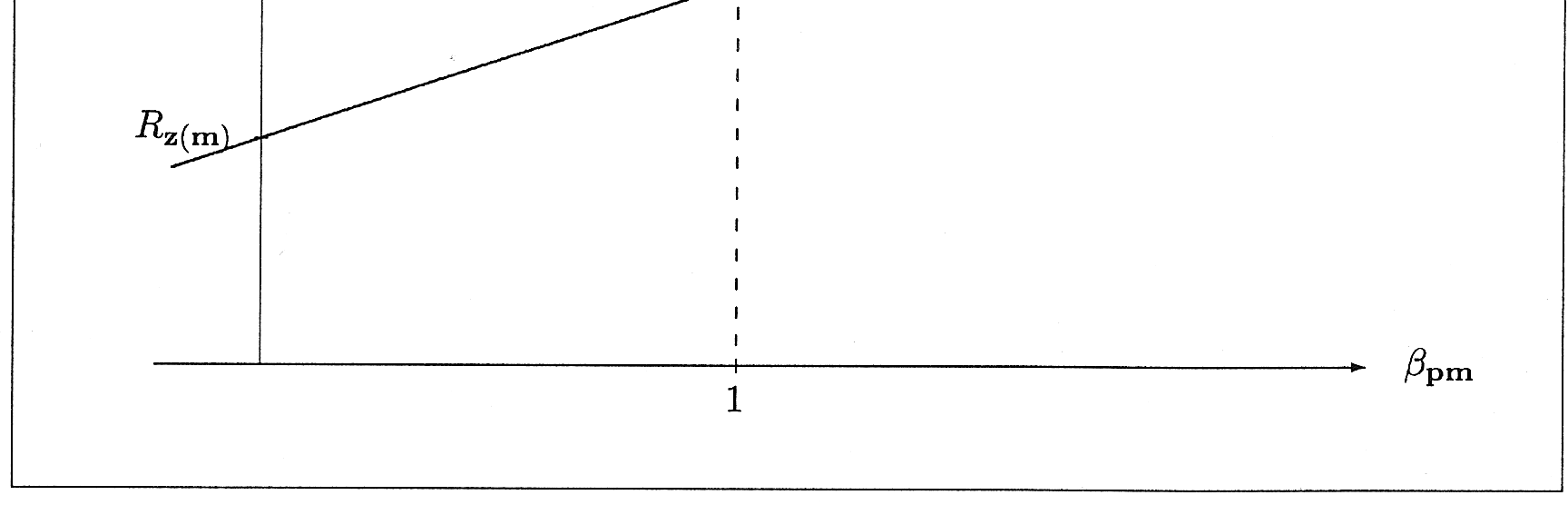
Podać można twierdzenie modelu Zero-Beta CAPM (Lintner 1969, Black 1972): Wartość oczekiwana stopy zwrotu każdego portfela p spełnia równanie R = R

+ β

( R − R

(*)

p

z ( m )

)

pm

m

z ( m)

6

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III gdzie

(**) R

− R

> 0

m

z ( m)

Nierówność (**) zachodzi ponieważ efektywność portfela m ( R

> R )

m

g

poci

( R

< R

ąga za sobą nieefektywność portfela z( m)

)

z ( m )

g

Dlaczego oczekiwana stopa zwrotu rośnie wraz ze współczynnikiem beta portfela?

• Dane są portfele p oraz q o identycznych wartościach oczekiwanych i wariancji.

• Niech portfel p posiada dodatnią korelację z portfelem rynkowym, portfel q –

ujemną.

7

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III

• Portfel p daje wysokie stopy zwrotu gdy gospodarka jest w stanie koniunktury, portfel q – odwrotnie, gdy jest w stanie dekoniunktury.

• Inwestorzy bardziej doceniają 1 jednostkę bogactwa w stanie dekoniunktury, niż w stanie koniunktury

• Portfel q jest zatem bardziej “doceniany” niż portfel p, zatem posiada większą cenę.

• Ponieważ wartości oczekiwane portfeli obliczane są jako ilorazy oczekiwanego zwrotu z portfeli i ceny portfeli to portfel p posiada większą oczekiwaną stopę zwrotu

8

dr J. Żarnowski, Teoria Inwestowania – materiały do wykładu – część III 9