)
)
3]
3]
2)
3)
1:
2:
,[1
,[2:
acierzy
2,
3,
3]
3]
(1:
(2:
([1
([1
ji m
A
A
A
A
v
i
b
e:
e:
e:
A
lu
j sekc
u
a:
ne
a
eceni
eceni
eceni
ierzy
da
ol
ol
ol
tor
sam
P
P
P
ac
a
m
ek
e do
n
w
7]
3
2
7
3
2
7
3
2
7
m
takć
6
ani
u
y
oł
ego
2
3
6
2
3
6
2
3
6
1
ol
dw
k
ow
si b
2;
O
1
5
1
1
5
1
1
5
1
a
u
ład
3
=
=
=
k
m
5
A
A
A
iczbL rzy
3;
p
2
]
1)
3)
2)
[1
; v’
]
(1,
(2,
(3,
:
]
3]
=
3
A
A
A
2
2
A
[A
go
e:
2
3;
=
u]
; 1
ne
acierzym
2[
[A
[A
3;[
eceni
A
=
=
=
=
:
ol
A
A
P
u
; u]
v
zczegól
:
[A
pos
3
2
7
iersza do
3
2
7
=
3
2
7
2
acierzy
acierzy
2
3
6
e w
2
3
6
2
3
6
2
e m
e do
m
e: A
u
1
5
1
ani
1
5
1
1
5
1
2
ierze
zeni
oł
ent
=
czanią
=
eceni
=
ac
or
oł
w
A
dw
A
ol
A
M
T
O
elem
D
P
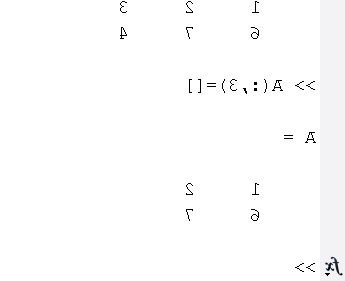
A
A
A
acierzy
acierzy
acierzy
męn iersz mw
:
um
iersz m
i 3
w
kol
:
a 2
:
3
2
7
]
]
v]
a 2
a 2
acierzy
uw
2
3
2
2
6
uw
uw
us
[A
3]
m
acierzy
us
us
acierzy
2
3;
=
;2;
1
2
1
ny
m
[1
=
um
[ ] -
2[
3;[
=
[ ] -
A
u
[ ] -
do
=
=
] A
=
u’
iersza m
, :) =
ny
u
v
w
, :) =
3
(: , 4)
, :) =
um
[A
A
go
]
(2
(: , 2)
(2:
3
2
(2
7
=
ne
3
2
7
2
iersza / kol
e kol
2
3
6
da
e: A
2
3
6
2
e: A
e w
e: A
e: A
e: A
1
5
1
iana
1
5
1
2[
ani
ierze
czani
eceni
eceni
eceni
ą
=
eceni
=
=
ol
ol
ol
ac
oł
eceni
suw
A
ol
P
ol
odm
P
P
A
u
P
U
M
D
P
P
2
1
1
+
+
n
n
n
+
1
2
m
b
b
b
4
0
+
+
2
M
+
1
1
+
+
+
n
n
n
1
2
4
6
m
a
2
a
a
+
+
+
0
5
1
0
h
3
2
1
m
ac
b
...
...
M
+
2
1
1
+
y
a
iar
3
+
+
m
2
0
, gd
iad
m
a
6
4
3
y
C
+
+
+
owp
roz
2
2
2
8
2
4
ted
1
2
m
b
b
b
2
4
1
w
ierzy
ch
+
+
M
+
+
+
+
y
o
ac
2
2
2
4
0
4
1
2
m
a
a
1
lk
a
szej od
sam
ty
ej m
2
1
1
ć
1
+
+
gi
ch
1
1
y
1
2
m
+
b
b
ierw
b
4
0
ż
ty
+
+
M
+
2
1
1
o
ru
+
+
p
+
n
d
1
1
1
1
2
m
a
a
2
a
8
4
1
+
+
om
w
ierzy
2
+
p
ierze o
=
2
5
a
ac
n
ac
n
n
n
=
ż
m
ierszy
1
2
M
o
m
m
b
b
b
n
B
o
A
m
3
u
ści w
:
lk
...
...
M
mb
ol
ilo
ty
ierze m
k
ć
B
5
1
2
1
a
2
2
2
ac
ść
1
2
M
m
b
b
acierzy
b
2
7
6
1
ow
M
ilo
1
1
e m
1
M
1
2
2
1
ejm
1
2
m
b
b
b
=
ani
±
B
ow
i odć
n
n
:
a
n 1
2
M
m
jm
a
a
a
8
6
3
aw
2
1
1
1
4
2
3
od
...
...
M
ma
acierzy
1
7
5
0
5
9
e i ode
d
4
9
4
a
A
e m
4
6
2
ani
n
2
2
2
ż
1
2
M
m
4
2
7
w
o
a
a
a
eni
1
3
1
ierze
ż
2
5
2
M
=
ac
oda
1
1
1
no
1
2
M
m
=
a
a
a
B
M
D
M
A
A
2
7
8
e:
1
−
−
2
7
8
’
1
−
−
A
6
eceni
2
3
1
−
2
ol
6
3
1
−
P
2
−
2
−
3
9
2
−
2
−
3
9
2
−
2
−
=
5
1
7
=
po
T
d
1
2
−
A
0
3
−
A
=
D
1
4
2
A
=
T A
2
1
8
2
3
7
−
2
−
4
0
1
9
3
7
−
ch
-1
2
−
A
1
2
5
po
−
T
d
6
e:
A
3
2
=
2
aiczny
=
−
1
−
br
A
D
eceni
=
:
A
ol
p
alge
P
od
eń
ana
A
3
7
:
łni
D
czona
0
1
ą
ji
na
A⋅
1
ponow
2
3
7
+
A
rot
1
)
A
=
1
1
−
et
4
0
1
(
d
2
=
acierz dope
T
=
acierz doł
1
5
−
1
m
ierze
ij
) 1
1
m
−
–
ac
acierz trans
A
acierz odw
–
p
ij
=
o
A
D
d
dop
M
M
M
A
A
A (
A
chty
a)w
ierze o
h
ty
ac
4)
m
ac
>
R
o
iar
lk
m
(A
0
0
0
czne
(alterna
ty
R
ce O
a
roz
) &
0
1
0
n
logi
O
zają
ż
B
y
o
chy
e
>
0
0
0
uc
czne
cja
m
ga
kl
ć
czn
(A
0
1
0
rator
y
a
sam
=
logi
ne
w
C
=
yw
logi
B
–
–
–
n
y
e:
k:
tałe ope
ów
or
ni
os
or
eceni
y
P
erat
ol
W
oz
P
|
~
xor
op
P
2
0
9
ne
ne
5
1
6
rówź
2
6
2
d
rów
ji
ą
2
3
4
0
1
0
0
0
1
ze lub
relac
=
0
1
0
1
0
1
y
ejsze b
ne
B
ks
ne
relacji
ni
ię
ż
or
B
1
0
0
B
0
0
0
y
m
w
rów
ró
2
1
1
>
<
–
–
–
–
erat
A
0
1
0
A
0
0
1
rator
B
B
B
B
op
1
7
5
=
=
=
=
=
=
=
=
B
B
<
>
=
~
4
6
2
e: C
e: C
A
A
A
A
k:
k:
tałe ope
=
=
=
=
ierze –
2
5
2
eceni
ni
ni
y
eceni
y
os
C
C
C
C
ac
=
ol
W
ol
W
oz
M
A
P
P
P


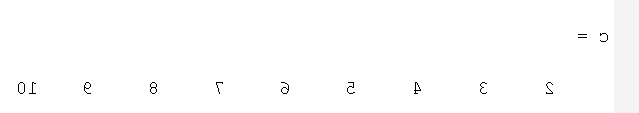
cńo kśćto
ar
: w
rok
: kz
oc
_p
eceń
ść
ol
to
p
for
a
ar
p
tla
w
ru
ęP
G
i =
d
for
en
ad
sz
raw
ifa
ow
jeśli p
jeśli fał
knu
)
eceń
eceń
ar
ol
ol
p
p
w
ekn
a
a
u
p
p
cja k
ar
ru
ru
(w
G
d
stru
if
else
G
en
In
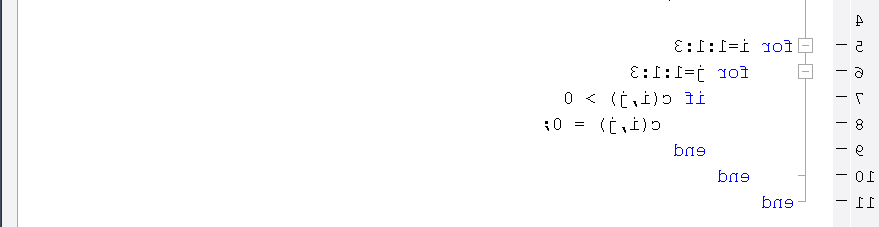
o dmy
czonąoł d
ogual lab
at
at
k
M
wy ietu
isan
ak p
zap
H
ć
T
y
A
si bu ej Pn
ien
cji mk zm
n
fu
ów
lik
lik
py
p”
zon
or
ie „m
wT
zen
orwT
a: A
acierzow
m
taćosP
ie
1
2
y
y
M
n
y
lab
=
at
Y
M
w
ń
1
2
M
n
a
x
x
x
n
1
2
n
y
y
y
=
e:
=
=
=
X
rów
n
n
n
x
x
x
atlabi
ów
n
n
n
1
2
n
a
a
a
n
n
n
1
2
M
n
M
ład
+
+
+
a
a
a
w
k
...
...
M
...
+
+
+
a:
...
...
M
...
adu
ie u
2
2
2
x
x
x
Y
an
2
2
2
2
2
M
1
2
1
2
n
*
w
2
n
a
a
a
a
a
a
e ukł
+
zy
+
+
acierzow
-1
1
1
1
1
^
\Y
ią
1
1
x
x
x
1
2
M
n
zani
1
m
a
a
a
A
A
w
1
1
1
ią
2
n
a
a
a
w
=
=
oz
tać
=
X
X
R
os
A
oz
P
R
Wyszukiwarka
Podobne podstrony:
Matlab Wyklad 2
SiPR wykład 2+matlab, W SPR Przykłady Kinematyka
wykład 5 +matlab, W SPR nr 03 04 Kinematyka Odwrotna
Mechanika Ogólna LAB.(Matlab) - 2 Rok, Politechnika, Sprawozdania, projekty, wyklady, Mechanika Ogol
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
Strategie marketingowe prezentacje wykład
Wykład 6 2009 Użytkowanie obiektu
więcej podobnych podstron



