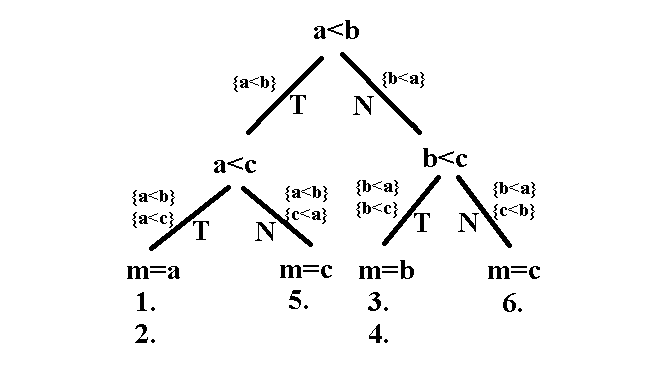
Przykład: znajdowanie liczby najmniejszej.

Wskazać najmniejszą spośród trzech różnych liczb: a, b, c.

Inne sformułowanie zadania:

Mając trzy różna liczby a,b,c, wyznaczyć liczbę m , tak aby m =a lub m = b lub m = c, przy czym m ≤ a , m ≤ b , m ≤ c.

Możliwe sytuacje:

1. a<b<c

2. a<c<b

3. b<a<c

4. b<c<a

5. c<a<b

6. c<b<a

Maszyna różnicowa Charlesa Babbage’a

Kolejne kwadraty Kolejne liczby nieparzyste 12 = 0 + 1 ←⎯⎯⎯ 1

22 = 1 + 3 ←⎯⎯⎯ 3 = 1 + 2

32 = 4 + 5 ←⎯⎯⎯ 5 = 3 + 2

42 = 9 + 7 ←⎯⎯⎯ 7 = 5 + 2

Aby policzyć kwadrat kolejnej liczby należy:

1. Ustawić liczby 0, 1 i 2 jako wartości początkowe 2. Wykonać dwa dodawania

• Dodać 2 dla uzyskania następnej liczby nieparzystej

• Dodać wynik do poprzedniego kwadratu

Systemy liczenia:

System dziesiętny:

- cyfry: 0,1,2,3,4,5,6,7,8,9

- postać liczby: Cn Cn-1 Cn-2 . . . C1 C0

- wartość liczby:

Cn*10n+Cn-1*10n-1+Cn-2*10n-2+ ...+C1*101+C0*100

System dwójkowy (binarny):

- cyfry: 0,1

- postać liczby: Bn Bn-1 Bn-2 . . . B1 B0

- wartość liczby:

Bn*2n+Bn-1*2n-1+Bn-2*2n-2+ ...+B1*21+B0*20

Postać binarna liczby dziesiętnej:

(13) 10= 8+4+1= 1*23+1*22+1*20 = 1*23+1*22+0*21+1*20

(13) 2= 1101

(191)10

191:2=95 r 1 ↑ (191)2 = 10111111

95:2=47 r 1 ⏐

47:2=23 r 1 ⏐ Sumowanie 23:2=11 r 1 ⏐ dziesiętne: binarne: 11:2=5 r 1 ⏐ 7 111

5:2=2 r 1 ⏐ + 5 +101

2:2=1 r 0 ⏐ 12 1100

1:2=0 r 1 ⏐

Maszyny podstawowe (bramki i sumatory):

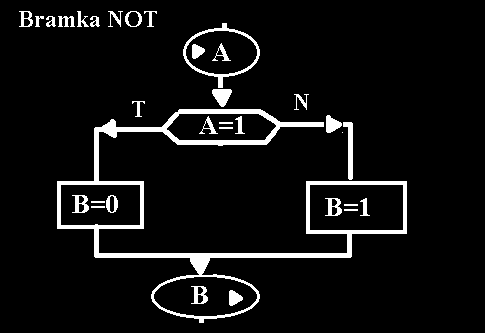
Bramka NOT:

Input (A) Output (B)

1

0

0

1

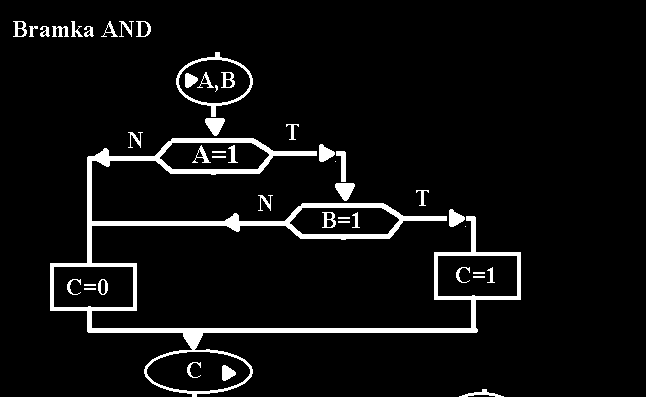
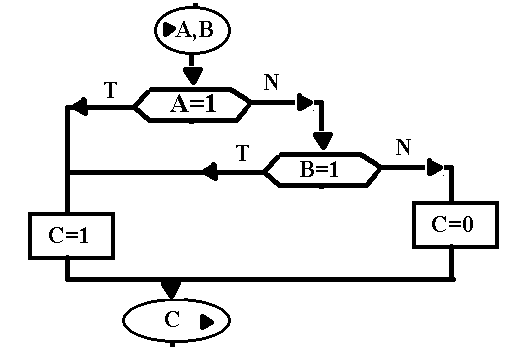
Bramka AND:

Input(A) Input(B) Output(C)

1 1 1

1 0 0

0 1 0

0 0 0

Bramka OR:

Input(A) Input(B) Output(C)

1 1 1

1 0 1

0 1 1

0 0 0

Bramka OR

Sumator dwójkowy jednopozycyjny:

Input(A) Input(B) Input(Z1) Output(C) Output(Z2) 0 0 0 0 0

0 0 1

0 1 0 1 0

1 0 0

1 1 0

0 1 1 0 1

1 0 1

1 1 1 1 1

Algorytm Euklidesa

Dane są dwie nieujemne liczby całkowite m , n . Liczba k=NWD(m,n) jest największym wspólnym dzielnikiem m i n jeśli dzieli m oraz n i jest największą liczbą o tej własności.

Algorytm Euklidesa znajduje największy wspólny podzielnik.

Załóżmy n ≥ m ⇒ n = q *m + r gdzie 0 ≤ r < m.

Stąd:

• Jeśli r = 0 to NWD(m,n)=m

Jeśli jedna z liczb dzieli drugą bez reszty to mniejsza z tych liczb jest największym wspólnym dzielnikiem.

• Jeśli r ≠ 0 to r = n – q*m

Każda liczba dzieląca n i m dzieli także r ⇒

NWD(m,n)=NWD(r,m) przy czym zgodnie z punktem

pierwszym NWD(0,m) = m.

Rozważmy liczby n=48, m=46.

48=1*46+2

46=23*2+0

czyli NWD(46,48)=NWD(2,46)=NWD(0,2) = 2

Zależność n = q *m + r zapewnia, że możemy generować pary liczb o tym samym największym wspólnym dzielniku, elementy tych par tworzą malejący ciąg liczb naturalnych.

Ciąg ten jest skończony, na jego końcu otrzymujemy szukany dzielnik.