PRACOWNIA FIZYCZNA U.Ś.
Nr ćwiczenia: 73	Temat: Wyznaczanie współczynnika załamania światła w szkle metodą kąta najmniejszego odchylenia
Imię i Nazwisko: Rafał Michniewicz
Rok studiów: I	Kierunek: Informatyka
Grupa: 17:45	Data wykonania ćwiczenia: 16 III 1999
Ocena: ......................

Światło przechodząc z jednego ośrodka do drugiego ulega załamaniu pod pewnym kątem na granicy ośrodków (wchodząc i wychodząc do pryzmatu załamuje się ku płaszczyźnie podstawy) Współczynnik załamania światła wyznaczyć możemy z kątów padania i załamania światła na granicy ośrodków. Najwygodniej w ty, celu posługiwać się ciałem o specjalnie dobranym kształcie. Najczęściej stosujemy pryzmat który jest bryła ograniczoną dwoma płaszczyznami tworzącymi ze sobą kąt ϕ zwany kątem łamiącym. Kształt pozostałych ścian nie odgrywa istotnej roli. Promień świetlny padający na pryzmat zostaje odchylony o pewien kąt α, zależny od kąta padania β i od kąta łamiącego ϕ. Kat α jest mniejszy gdy wewnątrz pryzmatu promień biegnie prostopadle do dwusiecznej kąta łamiącego. W tym przypadku kąt α jest równy sumie kątów nie przyległych w trójkącie ABC stworzonym przez przedłużenia promieni świetlnych.

zachodzi to wtedy gdy promień wewnątrz pryzmatu biegnie prostopadle do dwusiecznej kąta łamiącego, zatem

stąd można wyznaczyć szukane kąty α i β

współczynnik załamania wyznacza się wg wzoru

Pomiar kąta łamiącego pryzmatu następuje przez pomiar kąta załamania światła padającego na pryzmat prostopadle do podstawy pryzmatu. Wartości odczytuje się z lewej i z prawej strony. Właściwy kąt łamiący uzyskuje się ze wzoru:

gdzie:

α₁ - kąt załamania światła uzyskany z lewej strony pryzmatu

α₂ - kąt załamania światła uzyskany z prawej strony pryzmatu

z przekształcenia powyższego wzoru otrzymujemy

	γ1	γ2	γ'2=360°-γP	ϕ=(γ1+γ'2)/2
1	67°22'54''	307°22'52''	52°37'08''	60°00'01''
2	67°22'53''	307°22'53''	52°37'07''	60°00'00''
3	67°22'52''	307°22'51''	52°37'09''	60°00'0,5''
4	67°22'49''	307°22'57''	52°37'03''	59°59'56''
5	67°22'56''	307°22'54''	52°37'06''	60°00'01''
średnia	67°22'53''	307°22'53''	52°37'07''	59°59'59''

	ϕ=(γ1+γ'2)/2
1	60°00'01''	-0°00'1.3''	0°00'0.0005''
2	60°00'00''	-0°00'0.3''	0°00'0''
3	60°00'0,5''	-0°00'0.8''	0°00'0.0002''
4	59°59'56''	0°00'3.7''	0°00'0.0038''
5	60°00'01''	-0°00'1.3''	0°00'0.0005''
średnia	59°59'59''		0°00'0.001''

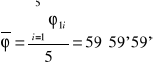
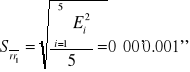
średnia wartość kąta łamiącego wynosi

pomiary kąta minimalnego odchylenia pryzmatu z lewej strony

	1. czerwony			2. żółty
1	321°32'50''	0°00'48''	0°00'0,6''	321°42'49''	-0°09'11''	0°01'24''
2	321°51'22''	-0°17'44''	0°05'14''	321°41'52''	-0°08'14''	0°01'07''
3	321°50'20''	-0°16'42''	0°04'38''	321°41'40''	-0°08'02''	0°01'04''
średnia	321°44'51''		0°03'18''	321°42'07''		0°01'12''

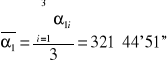
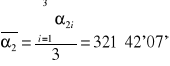
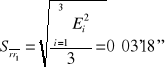
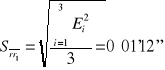
	3. zielony			4. niebieski
1	321°32'56''	0°00'42''	0°00'0,5''	321°15'30''	-0°18'08''	0°05'28''
2	321°32'52''	0°00'46''	0°00'0,6''	321°16'26''	-0°17'12''	0°04'55''
3	321°33'18''	-0°00'20''	0°00'0,1''	321°15'28''	-0°18'10''	0°05'30''
średnia	321°33'02''		0°00'0,4''	321°15'48''		0°05'18''

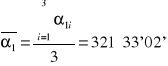
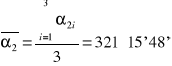
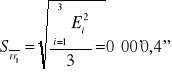
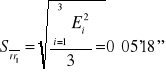
	5. turkusowy			6. fioletowy
1	320°50'22''	0°00'52''	0°00'0,8''	320°31'10''	0°00'31''	0°00'0,3''
2	320°51'48''	-0°00'33''	0°00'0,3''	320°33'28''	-0°01'46''	0°00'03''
3	320°51'34''	-0°00'19''	0°00'0,1''	321°30'26''	0°01'15''	0°00'1,6''
średnia	320°51'15''		0°00'0,4''	320°31'41''		0°00'01''

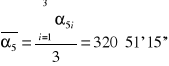
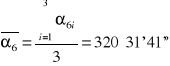
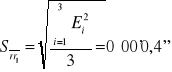
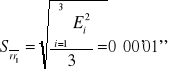
pomiary kąta minimalnego odchylenia pryzmatu z prawej strony

	1. czerwony			2. żółty
1	38°46'42''	0°07'05''	0°00'50''	39°06'42''	-0°00'14''	0°00'0,1''
2	38°57'24''	-0°03'36''	0°00'13''	39°06'34''	-0°00'06''	0°00'00''
3	38°57'16''	-0°03'28''	0°00'12''	39°07'08''	0°00'20''	0°00'0,1''
średnia	38°53'47''		0°00'25''	39°06'28''		0°00'0,1''

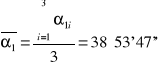
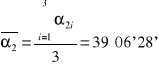
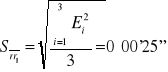
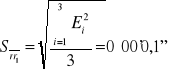
	3. zielony			4. niebieski
1	39°13'06''	0°00'22''	0°00'01''	39°32'06''	-0°00'10''	0°00'0,03''
2	39°14'06''	-0°00'38''	0°00'0,4''	39°31'52''	0°00'03''	0°00'0,0''
3	39°13'12''	0°00'16''	0°00'0,1''	39°31'48''	0°00'07''	0°00'0,01''
średnia	39°13'28''		0°00'0,2''	39°31'55''		0°00'0,02''

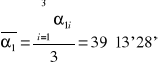
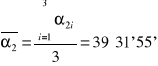
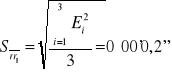
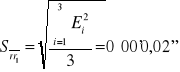
	5. turkusowy			6. fioletowy
1	40°00'06''	-0°02'10''	0°00'04''	40°15'22''	0°00'02''	0°00'0,0''
2	39°57'02''	0°00'53''	0°00'0,7''	40°15'02''	0°00'22''	0°00'0,1''
3	39°56'38''	0°01'17''	0°00'01''	40°15'48''	-0°00'24''	0°00'0,1''
średnia	39°57'55''		0°00'02''	40°25'24''		0°00'0,1''

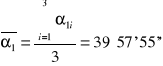
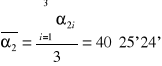
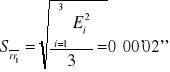
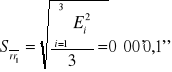
Kąt minimalnego odchylenia dla poszczególnych prążków oblicza się korzystając ze wzoru:

gdzie δ_sr i δ_sl to średnie wartości kątów z odpowiednio lewej i prawej strony dla danego prążka

	prążek	δsr	δsl	δmin
1	czerwony	38°53'47''	321°44'51''	38°34'28''
2	żółty	39°06'28''	321°42'07''	38°42'10''
3	zielony	39°13'28''	321°33'02''	38°50'13''
4	niebieski	39°31'55''	321°15'48''	39°08'03''
5	turkusowy	39°57'55''	320°51'15''	39°33'20''
6	fioletowy	40°25'24''	320°31'41''	39°56'51''

Obliczam współczynnik załamania dla poszczególnych długości fali, korzystając ze wzoru:

gdzie:

α - kąt padania wiązki światła na pryzmat, względem prostopadłej do płaszczyzny padania

β - kąt wiązki wychodzącej z pryzmatu, względem prostopadłej do płaszczyzny wychodzącej

powyższe kąty oblicza się ze wzoru:

gdzie:

δ_min - kąt minimalnego odchylenia

ϕ - kąt łamiący pryzmatu

	prążek	δmin	α
1	czerwony	38°34'28''	49°17'13''
2	żółty	38°42'10''	49°21'04''
3	zielony	38°50'13''	49°25'06''
4	niebieski	39°08'03''	49°34'01''
5	turkusowy	39°33'20''	49°46'39''
6	fioletowy	39°56'51''	49°58'25''

wstawiając do wzoru

powyższe obliczone dane otrzymuję współczynnik załamania światła dla poszczególnych prążków

β = 29°59'59''

	prążek	α	n
1	czerwony	49°17'13''	1,515981
2	żółty	49°21'04''	1,517441
3	zielony	49°25'06''	1,518965
4	niebieski	49°34'01''	1,522335
5	turkusowy	49°46'39''	1,527095
6	fioletowy	49°58'25''	1,531503

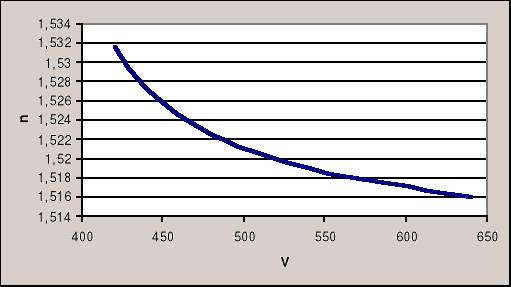
Ostatnim etapem zadania jest wyznaczenie wykresu krzywej dyspersji materiału z którego wykonano pryzmat.

Dyspersja jest to zależność współczynnika załamania pryzmatu od długości fali prążka

---