Krzysztof Cieślik 26 lutego 2000
Ćwiczenie 1
Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła różnicowego
Wstęp teoretyczny
- NATĘŻENIE POLA GRAWITACYJNEGO, PRZYSPIESZENIE ZIEMSKIE
Przyciąganie pomiędzy ciałami odbywa się za pośrednictwem pola grawitacyjnego (pola ciężkości), które na równi z innymi polami fizycznymi i substancjami jest jedną z postaci materii. Charakterystyczną właściwością pola grawitacyjnego jest to, że na umieszczony w nim punkt materialny działa siła ciężkości wprost proporcjonalna do masy tego punktu. Wektorowo opisuje się pole grawitacyjne za pomocą natężenia g, które jest równe stosunkowi siły ciężkości G działającej na punkt materialny do wartości jego masy m: ![]()
Swobodny spadek jest to ruch ciała, zachodzący pod wpływem tylko jego siły ciężkości. Przyspieszenie ziemskie grawitacyjne, (niekiedy zwane przyspieszeniem spadku swobodnego). jest jednakowe dla wszystkich ciał i zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Wartość przyspieszenia ziemskiego g (w m/s2) na niedużych wysokościach h (w metrach) n.p.m. można obliczyć ze wzoru przybliżonego: ![]()
cm/s2
W większości obliczeń technicznych pomija się zależność g od ϕ i przyjmuje się g=9,81 m/s2, zaś do wyznaczania zmiany g zachodzącej podczas oddalania się od powierzchni ziemi stosuje się wzór przybliżony: 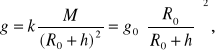
gdzie M - masa ziemi, R0=6370 km (średni promień Ziemi) zaś g0=9,81 m/s2
- RÓWNANIE RÓŻNICZKOWE OSCYLATORA HARMONICZNEGO
Drganiami harmonicznymi prostymi nazywamy drgania odbywające się pod wpływem siły F proporcjonalnej do wychylenia x i przeciwnie skierowanej. Zapisuje się to wzorem:
F= - kx
Współczynnik proporcjonalności k o wymiarze N/m nazywamy siłą kierującą.
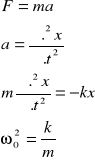
Wielkość ω0 nazywa się częstością kołową. Po podstawieniu i przekształceniu, otrzymujemy:
![]()
Równanie to nazywa się równaniem ruchu harmonicznego prostego. Jest ono równaniem różniczkowym drugiego rzędu względem zmiennej x.
![]()
![]()
![]()
Funkcja cosinus jest funkcją periodyczną i jej wartości powtarzają się co 2Π. Korzystając z powyższej własności i równania wyznaczyć możemy okres T, tzn. czas, po którym funkcja cosinus wraca do początkowej wartości:
![]()
skąd ![]()
Podstawiając za ω0 otrzymamy: ![]()
WAHADŁO RÓŻNICOWE
W wahadle różnicowym nie mamy podanej długości struny, na której jest zawieszony odważnik. Dokładniejsze wyniki pomiarów są, gdy będziemy rozpatrywać tylko i wyłącznie różnice, pomiędzy długością struny za pierwszym pomiarem, a drugim. Można w prosty sposób udowodnić, że nie potrzebujemy tej wartości.
Okres drgań w wahadle prostym wynosi: 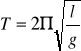
przy czym
l - długość wahadła
g - wartość przyśpieszenia Ziemskiego.
Zatem zakładając, że długość wahadła za pierwszym pomiarem jest równa l1, a za drugim l2 można uzyskać odpowiednie wzory:
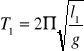
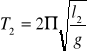
lub
![]()
![]()
Odejmując równania stronami otrzymujemy:
![]()
a z tego możemy
![]()
Wykonanie ćwiczenia
Moim zadaniem jest zmierzyć czas wahnięcia kulki przy dwóch różnych długości wahadła. Aby pomiar był dokładniejszy mierzymy czas 30 wahnięć, a następnie wyliczamy czas średni jednego wahnięcia. Wyniki te zostały przedstawione w poniższej tabeli:
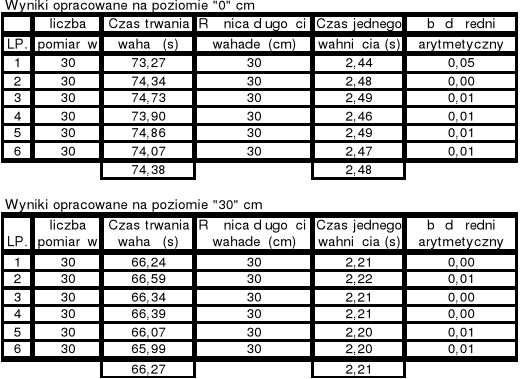
Powyższa tabela przedstawia serie wyników jakie zostały uzyskany w trakcie doświadczenia. Z pierwszej tabeli odrzucam pomiar pierwszy, ponieważ ma za dużą rozbieżność do pozostałych wyników i jak widać jego błąd wynosi 0,05 s (w pozostałych przypadkach różnice wynoszą do 0,01 s.).
Pod tabelami są podane wyniki obliczeń średnich wartości. Można przeczytać, że na poziomie „0 cm” średni czas wahnięcia wynosi 2,48 s. W uogólnieniu oznacza to, że czas jednego wahnięcia na poziomie 0 cm wynosi 2,48 ± 0,01 s. Zaś na poziomie 30 cm czas wahnięcia wynosi 2,21 ± 0,01 s.
Z tego możemy policzyć:
![]()
=
=4 ∗ (3,1415)2 ∗ 0,30/((2,48+2,21) ∗(2,48-2,21))=
=9,353 m/s2
Obliczam błąd jaki został popełniony podczas przeprowadzania ćwiczenia
Stosując metodę różniczki zupełnej obliczam błąd:
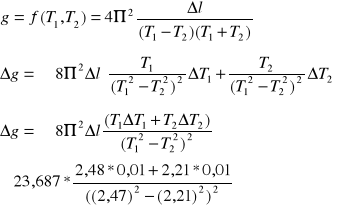
≈0,911 m/s2.
Mimo, że masa kulki nie ma wpływu na czas (a przez to na wyniki obliczenia przyciągania), to dodatkowym zadaniem było pomiar masy kulki. Dlatego też w czasie przeprowadzania ćwiczenia zmierzyłem dziesięciokrotnie średnicę kulki. wynosiła ona odpowiednio:
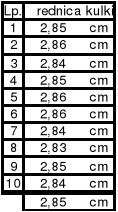
Poniżej jest podana średnia arytmetyczna wyników. oznacza to, że średnica kulki wynosi
2,85 mm ± 0,02 mm .
Podstawiając do wzoru możemy policzyć objętość kulki:
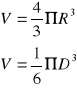
Mając obliczoną objętość możemy policzyć masę ze wzoru:
![]()
δ - gęstość
czyli
M=V∗δ
Podstawiając wzór do powyższego równania otrzymujemy:
![]()
Gęstość stali wynosi 7,8 ± 0,1 g/cm3
Rozbieżności te są spowodowane różnym stosunkiem żelaza do węgla.
Podstawiając do tego wzoru dane wyliczamy, że
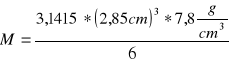
M=94,5 g
Określam błąd metodą pochodnej logarytmicznej:
![]()
![]()
![]()
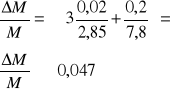
Błąd z tego po zaokrągleniu do góry wyliczony wynosi: ≈ 4,7 %
Wyszukiwarka
Podobne podstrony:
sprawdzone, Fiz 01 - wstęp teoretyczny, Ćwiczenie 1
sprawdzone, fiz 01 - opracowanie wyników, Opracowanie wyników
sprawdzone, Fiz 04a, ĆWICZENIE NR 4
sprawdzone, Fiz 04a, ĆWICZENIE NR 4
sprawdzone, Fiz 20 - wstęp teoretyczny, Ćwiczenie nr 20
01 cwiczenie 1
Grawimetria Kolos 1, Geodezja PW, Stare dzieje, Geod fiz + graw, Ćwiczenia
Lab fiz 01, fff, dużo
01, Cwiczenie 01 g, Laboratorium z fizyki
sprawdzone, Fiz 20, ˙I˙ PRACOWNIA FIZYCZNA U.˙.
sprawdzone, FIZ 60, Fotooporem (fotorezystorem) nazywa si˙ p˙˙przewodnik, kt˙rego op˙r zmienia si˙ p
sprawdzone, FIZ 50, Obwód wyidealizowany. Do biegunów A i B źródła prądu zmiennego przyłączony jest
sprawdzone, Fiz 73
01 Cwiczenie1id 2795 Nieznany (2)
01 cwiczeniaid 3060 ppt
01 Ćwiczenie
01 ĆWICZENIA
2010 01 Ćwiczenie 3 Ujemne sprzeżęnie zwrotne, wzmacniacz odwracający i nieodwracający
więcej podobnych podstron