Lista 2.
Całką Eulera drugiego rodzaju nazywa się całkę
Γ (p) = ![]()
xp-1 * e-x dx, dla x > 0 i p > 0 (p jest parametrem).
Całka istnieje i nazywa się ją funkcją gamma.
Pokazać, że:
a). Γ (p + 1) = p * Γ (p)
b). Γ (1) = 1
c). Γ (p + n) = n! dla p = 1.
Ponadto dla p = ½ Γ (½) = √π. Wykorzystując własności funkcji gamma obliczyć wartość całki
I = ![]()
![]()
e-![]()
x* dx, - ∞ < x < ∞
***
Podać rozkład zmiennej losowej, która przyjmuje wartości równe sumie oczek na dwóch kostkach do gry. Obliczyć P (5 ≤ x < ∞).
***
Zmienna losowa X przyjmuje wartości równe liczbom naturalnym k z prawdopodobieństwem
P (X = k) = k/(3k) ,
gdzie c jest liczbą stałą. Wyznaczyć c i obliczyć P ( X ≥ 4).
***
Dystrybuanta zmiennej losowej X dana jest wzorem:
F(x) = 
Obliczyć:
a). P ( 5 ≤ x ≤ 8)
b). P ( 5 ≤ x < 8)
c). P ( 5 < x < 8)
d). Określić funkcje prawdopodobieństwa f (x) tej zmiennej.
***
Mamy daną funkcję gęstości zmiennej losowej X:
f (x) = 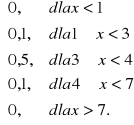
Znaleźć:
a). dystrybuantę F (x) zmiennej losowej X.
b). Obliczyć P(3,6 ≤ X ≤ 4,7).
c). Podać graficzną postać funkcji gęstości f (x) i dystrybuanty F (x).
***
Zmienna losowa X podlega rozkładowi według gęstości danej wzorem:
f (x) = 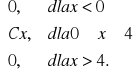
a). Obliczyć C.
b). Podać dystrybuantę.
c). Obliczyć P (1 ≤ x ≤ 2).
d). Podać wykres gęstości f (x) i dystrybuanty F (x).
***
Zmienna losowa X podlega rozkładowi według funkcji gęstości
f (x) = 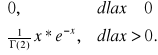
Obliczyć P (X > 1) i wyznaczyć dystrybuantę F(x) tej zmiennej.
***
Sprawdzić czy funkcja:
f (x) = 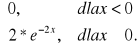
jest gęstością. Jeżeli tak, to wyznaczyć dystrybuantę F(x), obliczyć P (X ≤ - ½) i P (1 < X <2).
***
Zmienna losowa X ma rozkład według gęstości
f (x) = 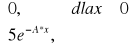
Wyznaczyć A i obliczyć P (X > 1), P (X = 1)
***
Gęstością prawdopodobieństwa zmiennej losowej X jest:
f (x) = 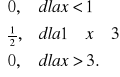
Znaleźć dystrybuantę F (x). Obliczyć P(x > 2), P(2 ≤ x ≤ 4). Podać interpretację tych prawdo- podobieństw na wykresie gęstości i dystrybuanty.
Wyszukiwarka
Podobne podstrony:
Rachunek Prawdopodobienstwa, listy 5-9, LISTA 5
Rachunek Prawdopodobienstwa, listy 5-9 sciaga, LISTA 5
Lista zadan do wykladu z Rachunku prawdopodobienstwa
Rachunek Prawdopodobienstwa, Rachunek-4 listy, I STATYSTYKA STOSOWANA, LISTA 1
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Matematyka - rachunek prawdopodbieństwa - ściąga, szkoła
09 Rachunek prawdopodobie ästwaid 7992
7 ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA
MATEMATYKA Rachunek prawdopodobieństwa, str tytułowa, Marcin Nowicki
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka dzienne wyklad1, Rachunek prawdopodobie˙stwa
1 zadania z rachunku prawdopodobieństwa, Zad
Zestaw10 rachunek prawdopodobie Nieznany
więcej podobnych podstron