Temat 5:
„Finansowe metody oceny.”
Wstęp.
Wybrane metody statyczne.
Wybrane metody dynamiczne.
Koszt kapitału w ocenie projektu.
Wstęp.
Skuteczne zarządzanie przedsiębiorstwem - to efektywne wykorzystanie kapitału m.in. poprzez wykorzystywanie metod oceniających racjonalność inwestycji (jako elementów rachunku inwestycji.
Rachunek inwestycji daje odpowiedź na pytania:
Czy realizacja planowanej inwestycji jest ekonomicznie opłacalna (ocena absolutna)?
Który z rozważanych wariantów inwestycji charakteryzuje się największą opłacalnością (ocena względna)?
W rachunkiem inwestycji bierze się pod uwagę:
nakłady inwestycyjne,
koszty operacyjne,
przychody z produkcji.
Podział metod rachunku inwestycji (kryterium: czas):
Metody statyczne:
wykorzystywane we wstępnych etapach oceny projektów (podstawa do orientacji w opłacalności projektu),
nieuwzględnianie czynnika czasu (jednakowe traktowanie przepływów strumieni pieniężnych w różnym czasie),
prostota użycia,
prosta interpretacja wyników.
Metody dynamiczne.
zaawansowany poziom oceny opłacalności projektu,
całościowe ujęcie czynnika czasu (rozkład wpływów i wydatków związanych z projektem),
wymagają gruntownej wiedzy z ekonomii i innych dziedzin (m.in. elementów matematyki finansowej).
Statyczne metody oceny inwestycji.
Metoda porównania kosztów.
Zastosowanie: wstępna ocena projektów w analizie kosztów działalności.
Informacje wejściowe:
dane dotyczące różnych rodzajów kosztów,
prognoza wielkości kosztów przyszłych inwestycji.
Założenia: warunki zewnętrzne (np. poziom zysku, cen, wielkość popytu) są stałe dla wszystkich analizowanych wariantów.
Wynik: ocena możliwości obniżenia kosztów pod wpływem różnych czynników wewnętrznych (m.in. rozmiaru produkcji, zbytu).
Stosowany podział kosztów:
Koszty wytwórcze - operacyjne (płace, materiały, remonty) - kw;
Koszty kapitałowe - inwestycyjne (amortyzacja, zysk kalkulacyjny) - kk.
Koszty kapitałowe.
Determinowane przez:
amortyzację - A,
zysk kalkulacyjny - Z.
Amortyzacja.
Dane:
długość okresu eksploatacji inwestycji (z założenia) - n lat,
poniesione nakłady inwestycyjne - M,
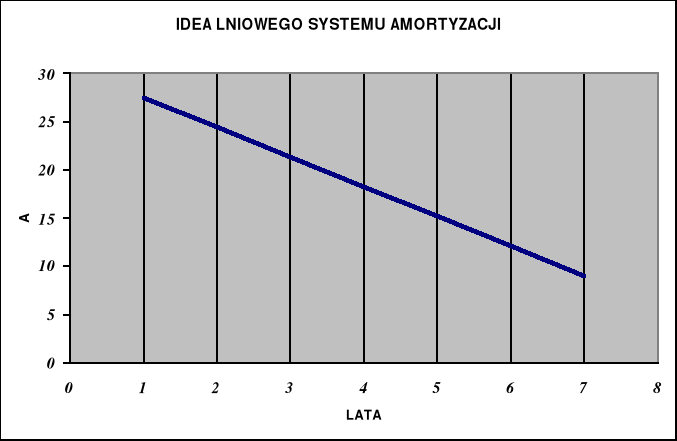
liniowy system amortyzacji środków trwałych (z założenia).
Amortyzacja A:
![]()
gdzie:
R - wartość określająca cenę, po jakiej można sprzedać majątek trwały po zakończeniu jego eksploatacji.
Zysk kalkulacyjny.
Zysk kalkulacyjny oznacza, ile można zyskać inwestując z i-tą stopą zwrotu kapitał Mp stanowiący średnią wielkość nakładów inwestycyjnych.
Założenia:
M - wielkość zainwestowanego wstępnie kapitału,
liniowy system amortyzacji.
Średnia wielkość nakładów inwestycyjnych Mp:
![]()
Zysk kalkulacyjny Z oblicza się z zależności:
![]()
Roczny koszt kapitałowy to suma amortyzacji i zysku kalkulacyjnego:
![]()
Uwzględniając koszt wytwórczy kw, całkowite koszty K wyznacza się z zależności:
![]()
Metoda porównania zysków.
Niech G oznacza zysk z nowej inwestycji, E - przychód, K - koszty. To:
![]()
Inwestycję jest opłacalna, jeśli
G > 0
Uwzględniając koszty jednostkowe zysk dla danego wariantu inwestycji wynosi:
![]()
gdzie:
p - jednostkowa cena sprzedaży,
x - wielkość produkcji,
kz - jednostkowe koszty zmienne,
Ks - całkowite koszty stałe.
Uwzględniając kryterium opłacalności:
G > 0
można określić minimalny poziom cen, przy którym dla zadanego poziomu produkcji x inwestycja będzie opłacalna:
![]()
![]()
![]()
Przykład.
W przedsiębiorstwie eksploatowane jest urządzenie, które jest całkowicie zużyte. Wynika stąd konieczność zakupu nowego. Dane umożliwiające ocenę opłacalności zakupu w tabeli, wiersze 1-5, 8, 10-12. Wykorzystując kryterium zysku, dokonać oceny opłacalności proponowanej inwestycji.
Charakterystyka inwestycji zakupu urządzenia.
L.p. |
Wyszczególnienie |
Inwestycja |
1 |
Nakłady inwestycyjne |
11 000 |
2 |
Wartość likwidacji |
0 |
3 |
Okres eksploatacji (w latach) |
10 |
4 |
Moc wytwórcza (w szt.) |
1200 |
5 |
Stopa kalkulacyjna (%) |
10 |
6 |
Amortyzacja (poz.1.-poz.2.)/poz.3. |
1 100 |
7 |
Oprocentowanie ((poz.1.+poz.2.)/2)*poz.5.) |
550 |
8 |
Pozostałe koszty stałe |
100 |
9 |
Razem koszty stałe |
1 750 |
10 |
Płace |
560 |
11 |
Materiały |
140 |
12 |
Pozostałe koszty zmienne |
110 |
13 |
Razem koszty zmienne |
810 |
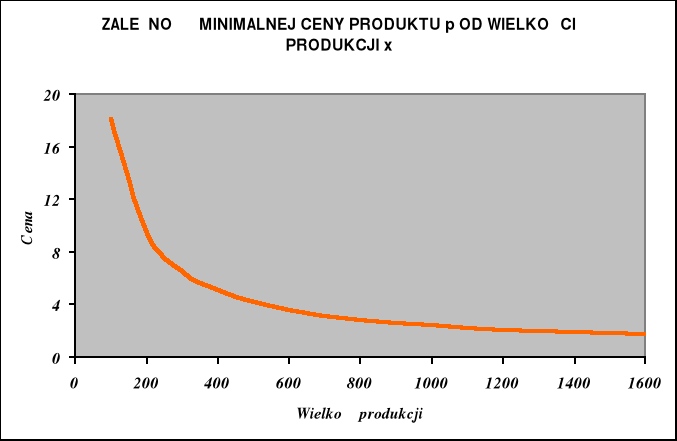
Rachunek inwestycji oparty będzie na analizie zależności minimalnej ceny towaru od wielkość produkcji:
![]()
Zależność powyższą dla różnych poziomów produkcji obrazuje wykres.
Dla produkcji na poziomie 200, minimalna cena zapewniająca opłacalność wynosi:
![]()
Uwaga: najmniejszy poziom cen zapewniający opłacalność inwestycji dla bardzo dużej produkcji nigdy nie będzie mniejszy niż wielkość jednostkowych kosztów zmiennych:
810/1200=0,675
Metoda porównania rentowności.
Rentowność inwestycji - stosunek zysku z inwestycji do zaangażowanego kapitału.
Roczna stopa zwrotu Re, wykorzystywana jako kryterium wyboru projektu jest definiowana:
![]()
gdzie:
G0 - zysk roczny uwzględniający wartość płaconych odsetek,
Mp - przeciętne zaangażowanie kapitału, zdefiniowane zależnością (jak poprzednio):
![]()
(M - poniesione nakłady inwestycyjne, R - cena, po jakiej można sprzedać majątek trwały po zakończeniu jego eksploatacji).
Kryterium wyboru projektu inwestycyjnego (warunek opłacalności projektu):
![]()
gdzie:
Remin - minimalny, dopuszczalny poziom rentowności.
W przypadku wielu projektów wybór dotyczy projektu o największej wartości wskaźnika rentowności Re nie mniejszej od zadanego poziomu minimalnego.
W przypadku, gdy zysk z inwestycji jest zróżnicowany w kolejnych latach, rentowność Re liczy się, jako średnią arytmetyczną rentowności Ri z poszczególnych lat (i=l,2,... n):
![]()
gdzie:
Gt - zysk osiągnięty w i-tym roku,
Mi - wielkość zaangażowanego kapitału w i-tym roku.
Dynamiczne metody oceny inwestycji.
Metoda wartości bieżącej - NPV (ang. Net Present Value).
Jedna z podstawowych metod uwzględniających w ocenach inwestycyjnych czynnik czasu.
Porównuje ze sobą poniesione obecnie nakłady z wartością bieżącą przyszłych przychodów z inwestycji.
Formuła obliczeniowa:
![]()
gdzie:
CF - strumień środków pieniężnych (ang. Cash Flow),
i - zakładana w obliczeniach stopa dyskontowa,
M - wartość poniesionych obecnie nakładów inwestycyjnych,
n - długość trwania projektu.
Założenia:
nakłady są ponoszone tylko w momencie rozpoczęcia inwestycji,
w okresie eksploatacji projektu następuje pełna jego amortyzacja (wartość umorzeniowa jest równa zero).
W przypadku pojawiania się nakładów w okresach późniejszych należy je zdyskontować (podobnie jak wpływy), traktując je jako ujemne.
Inwestycja jest opłacalna wtedy, gdy NPV jest większe od zera.
W przypadku wielu wariantów inwestycji, wybiera się ten, który charakteryzuje się największą dodatnią wartością wskaźnika.
Przykład.
Firma zamierza kupić urządzenie za 20 tys. zł. Jego eksploatacja zapewni firmie corocznie przepływ środków pieniężnych w wysokości 5000 zł przez 5 lat.
Czy przy zakładanej stopie procentowej 10% zaangażowanego kapitału inwestycja jest opłacalna dla firmy?
Zestaw danych:
wartość poniesionych nakładów inwestycyjnych M=20000zł,
strumień środków pieniężnych CF=5000,
długość trwania projektu n=5.
Wstawiając je do (5.3.1) otrzymujemy:
Rozwiązanie:
![]()
INWESTYCJA NIEOPŁACALNA (NPV < 0!)
Opłacalność inwestycji zapewni przepływ środków pieniężnych w wysokości nie mniejszej niż 5276 zł.
DLACZEGO?
Metoda wewnętrznej stopy zwrotu - IRR (ang. Internal Rate of Return).
Dla inwestora interesujące jest, przy jakiej wartości stopy dyskontowej i zwróci się w zakładanym okresie zainwestowany kapitał.
Wewnętrzna stopa zwrotu (IRR) - to taka stopa dyskontowa, przy której zwróci się (w zakładanym okresie eksploatacji projektu) zainwestowany kapitał przy założeniu, że przepływy środków pieniężnych z inwestycji są reinwestowane według stopy IRR.
Formalnie IRR oznacza taką wartość stopy procentowej i, dla której NPV jest równe zero czyli zachodzi zależność:
![]()
Projekt jest opłacalny z punktu widzenia wskaźnika IRR, jeśli jego wartość będzie większa od wymaganej stopy zwrotu i z inwestycji.
Przykład.
Wykonać kompleksową analizę finansową trzech wariantów projektu wykorzystując metody: NPV oraz IRR.
Charakterystyka rozważanych trzech wariantów inwestycyjnych.
Dane wejściowe |
Wariant I |
Wariant II |
Wariant III |
|
Nakłady inwestycyjne (M) |
150 |
60 |
45 |
|
Kalkulowana stopa procentowa (i) |
10% |
10% |
10% |
|
Okres eksploatacji (n) |
5 |
3 |
5 |
|
Dochody netto w poszczególnych latach |
1 |
50 |
40 |
20 |
|
2 |
40 |
30 |
15 |
|
3 |
40 |
10 |
10 |
|
4 |
40 |
|
10 |
|
5 |
40 |
|
10 |
Rozwiązanie:
W wyniku zastosowania odpowiednich zależności należy obliczyć: NPV, IRR.
Ocena rozważanych wariantów inwestycyjnych.
Metoda |
Wariant I |
Wariant II |
Wariant III |
IRR |
12,87% |
19,94% |
16,09% |
NPV |
10,7224 |
8,6702 |
6,1310 |
Wnioski z wyników:
Z punktu widzenia NPV - najlepszy jest wariant I;
Z punktu widzenia IRR najbardziej opłacalnym jest wariant II.
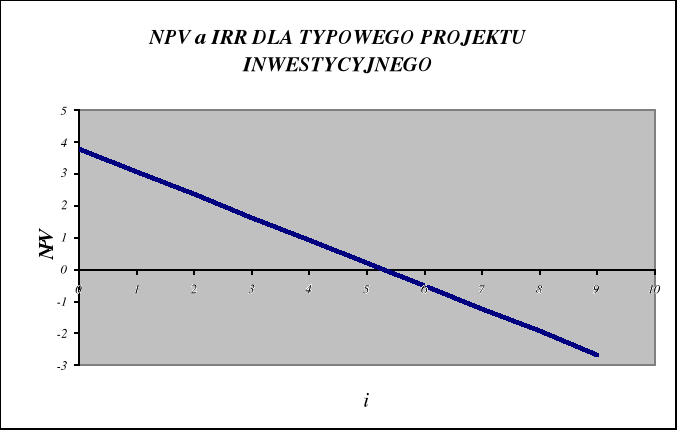
Porównanie metod wartości bieżącej - NPV i wewnętrznej stopy zwrotu - IRR.
W przypadku oceny opłacalności jednego projektu, metoda IRR stanowi uzasadnienie uzyskanych wartości NPV. Dla takiego przypadku występuje charakterystyczna zgodność obu miar.
Wnioski:
dla wszystkich stóp dyskontowych i < IRR, wartość NPV > 0;
dla stóp dyskontowych i > IRR, wartość NPV < 0.
Zatem:
Jeżeli kryterium NPV jest spełnione,
kryterium IRR również będzie spełnione.
Tylko projekty, które posiadają IRR większe niż stopa dyskontowa (IRR > i) (która traktowana jest jako koszt zaangażowanego kapitału) mogą być zaakceptowane. Odpowiada to regule, że opłacalne są tylko projekty o NPV > 0.
Koszt kapitału w ocenie inwestycji.
WACC - średni, ważony koszt każdej pozyskanej jednostki pieniężnej z przeznaczeniem na finansowanie działalności przedsiębiorstwa.
Wniosek: w ocenie inwestycji „WACC” nie powinien być średnim kosztem pieniądza pozyskanego w przeszłości.
W przypadku inwestycji, przedmiotem zainteresowania jest koszt kapitału możliwego do zastosowania.
Stosuje się pojęcie KOSZTU KRAŃCOWEGO MCC (ang. Marginal Capital Cost).
MCC oznacza koszt ostatniego wyposażenia kapitałowego (wzrost podwyższonego kapitału):
Szacować trzeba koszt każdej jednostki pieniężnej, którą firma pozyskuje w trakcie trwania inwestycji z przeznaczeniem na jej finansowanie.
Przykład.
Założenia:
firma ABC ma docelową (optymalną) strukturę kapitału:
dług - 30%,
kapitał akcyjny uprzywilejowany - 5%,
kapitał akcyjny zwykły - 65%;
(Skrótowy zapis takiej struktury: 30/5/65);
koszty poszczególnych składników kapitału:
koszt długu przed opodatkowaniem: io=11%,
koszt kapitału akcyjnego uprzywilejowanego: iu=10,3%,
koszt kapitału pochodzącego z zysków nie podzielonych: iw=14%,
koszt nowego kapitału akcyjnego: izn=15%;
krańcowa stopa podatku dochodowego: T=30%.
Spółka chce pozyskać 100 zł. Dla zachowania docelowej struktury kapitału, na 100 zł składać się powinno:
dług - 30 zł,
kapitał akcyjny uprzywilejowany 5 zł,
kapitał akcyjny zwykły 65 zł.
WACC dla tych 100 zł (firma kapitał akcyjny zwykły otrzyma z zysków nie podzielonych) wynosi:
WACC = 0.3*11%*(1-0.3)+0.05*10.3%+0.65*14% = 11.925%.
Z założenia: optymalna struktura kapitału wynosi 30/5/65, tzn. że każda nowa jednostka pieniężna powinna składać się z 30gr długu, 5gr kapitału akcyjnego uprzywilejowanego oraz 65gr kapitału akcyjnego zwykłego otrzymanego albo w formie zysków nie podzielonych albo poprzez emisję nowych akcji zwykłych.
Z przykładu: koszt kapitału wynosi 11,925%.
Nie można w sposób nieograniczony zdobywać kapitału o takim koszcie:
pozyskiwanie coraz większych środków pieniężnych wiąże się ze wzrostem kosztu długu oraz kosztu kapitału akcyjnego w efekcie powodując wzrost WACC.
Przykład.
Jeśli firma ABC zdobywa kapitał akcyjny zwykły z zysków nie podzielonych - koszt kapitału wynosi
WACC = 11,925%.
Jeśli firma w celu pozyskania większych środków wyemituje nowe akcje, WACC wyniesie (przy założeniu zachowania optymalnej struktury kapitału):
WACC = 0,3*11%*(1-0,3)+0,05*10,3%+0,65*15% = 12,575%.
Interpretacja:
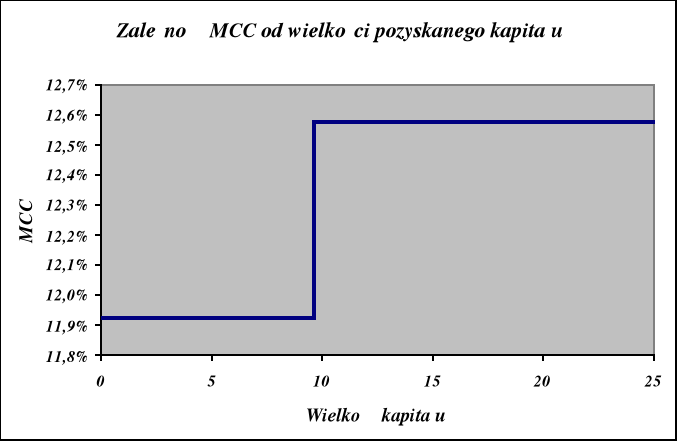
do momentu, kiedy zyski nie podzielone będą wystarczały, średni koszt kapitału wynosić będzie 11.925%,
w momencie emisji nowych akcji, średni koszt wzrośnie do 12.575%.
W jakim momencie nastąpi zmiana kosztów kapitału?
Założenie: firma planuje osiągnąć zyski na poziomie 10 mln zł, z czego 37% chce wypłacić akcjonariuszom w formie dywidendy.
W tym przypadku stopa zysków nie podzielonych wynosi:
1-0,37% = 0,63%
czyli planuje się zasilenie kapitału akcyjnego z zysków nie podzielonych w wysokości
0,63% * 10 mln= 6,3mln zł.
Dla zachowania założonej struktury kapitału 30/5/65 dla 6,3 mln kapitału zwykłego, firma może pozyskać całkowity kapitał w wysokości:
0,65 * x = 6,3 mln ⇒ x = 6,3/0,65 = 9,69 mln zł.
Interpretacja:
Dla założonych danych, przy zachowaniu optymalnej struktury kapitału firma może pozyskać łącznie 9,69 mln zł kapitału o średnim koszcie 11,925%.
Wielkość poszczególnych składników kapitału pozyskanego po koszcie
11,925%:
Składowa |
Wartość (w mln zł) |
Udział (w %) |
Dług |
2,91 |
30 |
Kapitał akcyjny uprzywilejowany |
0,48 |
5 |
Kapitał akcyjny zwykły |
6,30 |
65 |
RAZEM |
9,69 |
100 |
W procesie planowania inwestycji decydent ma do czynienia z zestawem potencjalnych projektów. Z każdym wiąże się konieczność oszacowania przepływów środków pieniężnych, a więc problem kosztu kapitału:
Zidentyfikowanie jaki powinien być krańcowy koszt kapitału do dyskontowania środków pieniężnych projektów, czyli którą z wartości WACC trzeba uwzględnić w ocenie projektów.
Odpowiedź na podstawie koncepcji analizy krańcowej:
Firma powinna rozwijać produkcję tak długo, dopóki przychód krańcowy nie będzie równy kosztowi krańcowemu.
Wtedy ostatnia jednostka produktu pokryje poniesione koszty.
To podejście w procesie inwestycyjnym wymaga zbudowania krzywej kosztów krańcowych MCC, i reprezentującej oczekiwaną stopę dochodu z każdej możliwej inwestycji tzw. krzywej możliwości inwestycyjnych IOS (ang. Investment Opportunity Schedule).
Przykład.
Firma ABC ma możliwość wykorzystania środków pieniężnych pochodzących z amortyzacji w wysokości 30 mln zł. Rozpatrywane są projekty o stopach dochodu jak w tabeli.
Charakterystyka potencjalnych projektów inwestycyjnych.
Projekt |
Koszt w realizacji |
Stopa dochodu (IRR) |
A |
30 |
16 |
B |
25 |
14 |
C |
40 |
13,6 |
D |
35 |
11 |
Określić koszt kapitału, który można wykorzystywać do dyskontowania środków pieniężnych analizowanych projektów.
Do rozwiązania problemu należy porównać:
koszt krańcowy (MCC) i
możliwości inwestycyjne (krzywą IOS).
Oszacowany wcześniej koszt krańcowy pozyskania kapitału to:
11.925% do wysokości 9.69 mln zł ,
12.575% powyżej 9.69 mln zł.
Uwzględniając, że:
firma może pozyskać 30 mln zł środków z amortyzacji,
środki te charakteryzują się takim samym kosztem co WACC przed wykorzystaniem nowych zewnętrznych źródeł.
Firma ABC może pozyskać kapitał w wysokości:
do 30 +9,69 = 39,69 mln zł po koszcie 11,925%,
powyżej 39,69 mln zł po koszcie 12,575%.
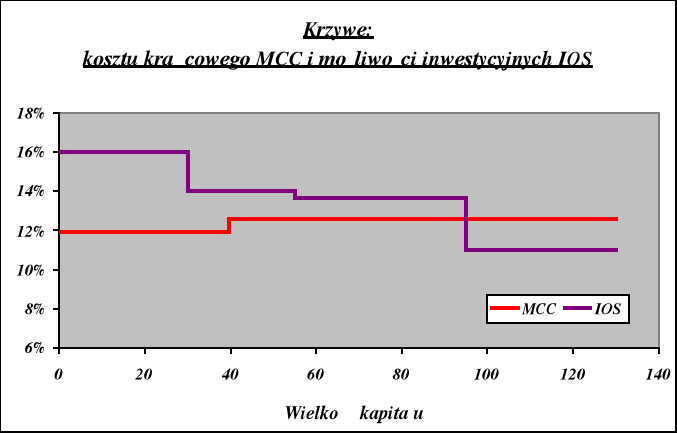
Projekty A, B i C mają oczekiwane stopy dochodu wyższe niż koszt kapitału wykorzystywany do ich finansowania. Projekt D ma koszt niższy.
Wniosek:
Za koszt kapitału wykorzystywany do oceny projektów inwestycyjnych należy przyjąć tą wartość WACC, która odpowiada punktowi przecięcia się krzywych MCC i IOS.
A więc: WACC = 12,575%.
Do realizacji należy wybrać projekty o wyższej stopie dochodu niż koszt kapitału: projekty A, B i C.
Koszt kapitału na poziomie 12,575% stanowi punkt odniesienia dla analiz projektów charakteryzujących się. ryzykiem innym niż przeciętne.
Koszt kapitału firmy - punkt przecięcia się krzywych MCC i IOS.
Tak wyznaczony koszt kapitału daje pewność, że decyzje o wyborze inwestycji i ich finansowaniu będą optymalne.
Koszt ten jest z reguły różny (większy) od średniego kosztu kapitału pozyskanego do finansowania projektów.
Uwzględnienie w analizach innego kosztu kapitału prowadzi do podejmowania decyzji nieoptymalnych.
Dr inż. Jerzy GOGOLEWSKI „METODY OCENY PROJEKTÓW GOSPODARCZYCH”
Wykład 5: „Finansowe metody oceny.”
Slajd 20
95 mln
B-11%
B-13,6%
B-14%
A-16%
12,6%
11,9%
9,69 mln (punkt pełnego wykorzystania zysków nie podzielonych)
WACC2=12,575%
WACC1=11,925%
i1
Kz=0,675
(M-R)/n
R
M
i2
NPV(i2)
NPV(i1)
IRR
Wyszukiwarka
Podobne podstrony:
Metody oceny, W4 Finansowanie, Email Template
Metody oceny, W6 Metody ekonomiczne, Email Template
Metody oceny, W1 Ocena a zarzadzanie, Email Template
Metody oceny, W2 Ryzyko, Email Template
Metody finansowania jednostek sektora fin
E Strategie i metody finansowania przedsiebiorstw Ryzlak
Metody finansowania organizacji społecznych
W5 System finansowy
MET, Email Template
Test Wydz.Lek. I wersja, Email Template
w5 zapasy, Finanse publiczne
Outreach Email Templates
w5 zarzadzanie finansami
więcej podobnych podstron