I. Metoda programowania nieliniowego PNL.

Celem ćwiczenia jest zapoznanie się z podstawową metodą rozwiązywania nieliniowego zadania optymalizacji bez ograniczeń na przykładzie algorytmu optymalizacji lokalnej (algorytm Gauss'a - Seidla lub algorytm Fletchera - Powella - Dawidona) lub algorytmu optymalizacji globalnej (algorytm genetyczny lub algorytm ewolucyjny).

Algorytm optymalizacji lokalnej lub algorytm optymalizacji globalnej pozwala na wyliczenie takiego wektora zmiennych decyzyjnych x, dla którego funkcja celu osiąga minimum:

bez ograniczeń:

--> Wstęp teoretyczny (na postawie informacji zawartych na stronie: http://pl.wikipedia.org)[Author:M]

Algorytm genetyczny to rodzaj algorytmu przeszukującego przestrzeń alternatywnych rozwiązań problemu w celu wyszukania rozwiązań najlepszych. Sposób działania algorytmów genetycznych nieprzypadkowo przypomina zjawisko ewolucji biologicznej, ponieważ ich twórca John Henry Holland właśnie z biologii czerpał inspiracje do swoich prac.

Najczęściej działanie algorytmu przebiega następująco:

1. Losowana jest pewna populacja poczÄ…tkowa.

2. Populacja poddawana jest ocenie (selekcja). Najlepiej przystosowane osobniki biorą udział w procesie reprodukcji.

3. Genotypy wybranych osobników poddawane są operatorom ewolucyjnym:

1. są sobą kojarzone poprzez złączanie genotypów rodziców (krzyżowanie),

2. przeprowadzana jest mutacja, czyli wprowadzenie drobnych losowych zmian.

4. Rodzi się drugie (kolejne) pokolenie i algorytm powraca do kroku drugiego, jeżeli nie znaleziono dostatecznie dobrego rozwiązania. W przeciwnym wypadku uzyskujemy wynik.

Działanie algorytmu genetycznego obejmuje kilka zagadnień potrzebnych do ustalenia:

1. ustalenie genomu jako reprezentanta wyniku

2. ustalenie funkcji przystosowania/dopasowania

3. ustalenie operatorów przeszukiwania

--> II. Zadania do wykonania[Author:M]

II.1 Funkcje wypukłe

1. f(x) = (x₁ - 2)² + (x₂ - 2)²

Punkt optymalny: x* = [2, 2]

Wartość optymalna funkcji: f(x*) = 0

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Zakres zmiennych: x₁ = [-5, 5]

x₂ = [-5, 5]

Porównanie rodzajów selekcji

Selekcja: miękka

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 102 generacjach)

Punkt optymalny: x* = [2.035, 2.033]

Wartość optymalna funkcji: f(x*) = 2,228 · 10^-3

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	1,384	2,114	0,393
2	1,744	2,172	9,48·10^-^2
5	1,917	2,256	7,24·10^-^2
10	1,809	1,859	5,62·10^-^2
20	2,000	1,991	7,34·10^-^3
>20	2,000	1,991	7,34·10^-^3

Punkt optymalny: x* = [2, 1.991]

Wartość optymalna funkcji: f(x*) = 7,34 · 10^-3

Selekcja: twarda

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 137 generacjach)

Punkt optymalny: x* = [2, 2]

Wartość optymalna funkcji: f(x*) = 0

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	3,311	1,750	1,782
10	2,003	2,006	4,87·10^-^5
20	2,003	1,998	1,09·10^-^5
30	2,003	2,000	8,09·10^-^6
>30	2,003	2,000	8,09·10^-^6

Punkt optymalny: x* = [2.003, 2]

Wartość optymalna funkcji: f(x*) = 8,09 · 10^-6

Selekcja: turniejowa

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 160 generacjach)

Punkt optymalny: x* = [2, 2]

Wartość optymalna funkcji: f(x*) = 0

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	1,699	2,510	0,351
10	2,003	1,999	9,47·10^-^6
20	2,000	2,000	1,22·10^-^7
30	2,000	2,000	7,98·10^-^8
40	2,000	2,000	5,81·10^-^9
50	2,000	2,000	3,60·10^-^11
>50	2,000	2,000	0

Punkt optymalny: x* = [2, 2]

Wartość optymalna funkcji: f(x*) = 0

Wizualizacja rozwiÄ…zania:

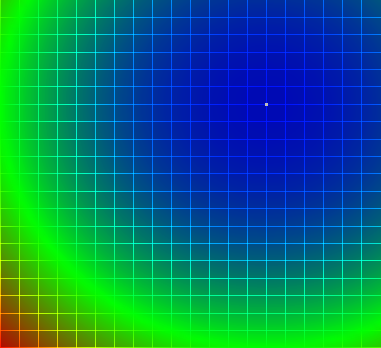
Część analityczna:

f(x) = (x₁ - 2)² + (x₂ - 2)²

2. f(x) = 2x₁² - 2x₁x₂ + x₂²

Punkt optymalny: x* = [0, 0]

Wartość optymalna funkcji: f(x*) = 0

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Zakres zmiennych: x₁ = [-2, 2]

x₂ = [-2, 2]

Porównanie rodzajów selekcji

Selekcja: miękka

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 104 generacjach)

Punkt optymalny: x* = [-1.177·10^-2, 1.159·10^-2]

Wartość optymalna funkcji: f(x*) = 1.387 · 10^-4

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	0,266	0,582	0,171
10	0,050	0,083	3,60·10^-^3
20	0,017	-0,022	1,80·10^-^3
30	0,017	-0,022	1,80·10^-^3
40	0,003	0,043	1,67·10^-^3
70	0,011	0,023	2,71·10^-^4
>70	0,011	0,023	2,71·10^-^4

Punkt optymalny: x* = [0.011, 0.023]

Wartość optymalna funkcji: f(x*) = 2,71 · 10^-4

Selekcja: twarda

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 137 generacjach)

Punkt optymalny: x* = [4.69·10^-7, 9.39·10^-7]

Wartość optymalna funkcji: f(x*) = 4.397 · 10^-13

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	0,061	0,520	0,214
10	0,012	0,012	1,52·10^-^4
>10	0,012	0,012	1,52·10^-^4

Punkt optymalny: x* = [0.012, 0.012]

Wartość optymalna funkcji: f(x*) = 1,52 · 10^-4

Selekcja: turniejowa

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 160 generacjach)

Punkt optymalny: x* = [1.242·10^-8, 1.425·10^-8]

Wartość optymalna funkcji: f(x*) = 1.576 · 10^-16

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	0,064	0,429	0,137
10	0,197	0,429	9,24·10^-^2
20	-0,039	-0,062	2,04·10^-^3
30	-0,039	-0,039	1,51·10^-^3
>30	-0,039	-0,039	1,51·10^-^3

Punkt optymalny: x* = [-0,039, -0,039]

Wartość optymalna funkcji: f(x*) = 1,51 · 10^-3

Wizualizacja rozwiÄ…zania:

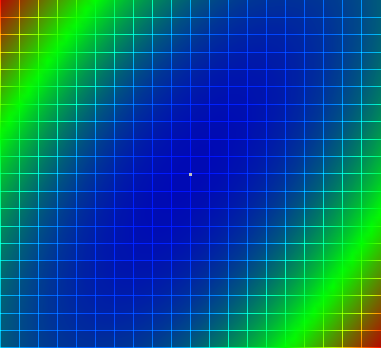
Część analityczna:

f(x) = 2x₁² - 2x₁x₂ + x₂²

3. f(x) = x₁² + x₁x₂ + 0.5x₂² - x₁ - x₂

Punkt optymalny: x* = [0, 1]

Wartość optymalna funkcji: f(x*) = -0.5

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Zakres zmiennych: x₁ = [-2, 2]

x₂ = [-2, 2]

Porównanie rodzajów selekcji

Selekcja: miękka

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 89 generacjach)

Punkt optymalny: x* = [0.039, 0.945]

Wartość optymalna funkcji: f(x*) = -0.499

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	0,133	0,922	-0,489
10	-1,36·10^-^3	1,030	-0,499
20	-1,36·10^-^3	1,030	-0,499
30	-1,36·10^-^3	1,030	-0,499
40	-1,36·10^-^3	1,030	-0,499
50	-1,36·10^-^3	1,030	-0,499
60	1,29·10^-^4	0,984	-0,5
70	1,29·10^-^4	0,984	-0,5
80	7,62·10^-^3	1,002	-0,5
>80	7,62·10^-^3	1,002	-0,5

Punkt optymalny: x* = [7,62·10^-3, 1,002]

Wartość optymalna funkcji: f(x*) = -0.5

Selekcja: twarda

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 93 generacjach)

Punkt optymalny: x* = [-2.22·10^-9, 1]

Wartość optymalna funkcji: f(x*) = -0.5

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	0,112	0,603	-0,453
10	-0,010	1,008	-0,499
20	-9,44·10^-^5	1	-0,5
30	-1,11·10^-^6	1	-0,5
40	9,40·10^-^9	1	-0,5
50	-3,44·10^-^9	1	-0,5
>50	-3,44·10^-^9	1	-0,5

Punkt optymalny: x* = [-3,44·10^-9, 1]

Wartość optymalna funkcji: f(x*) = -0.5

Selekcja: turniejowa

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 134 generacjach)

Punkt optymalny: x* = [-2.22·10^-9, 1]

Wartość optymalna funkcji: f(x*) = -0.5

Kryterium stopu: liczba generacji

generacja	x1	x2	optimum
1	8,40·10^-^2	0,857	-0,495
10	2,11·10^-^2	0,982	-0,499
20	2,49·10^-^3	0,998	-0,5
30	4,35·10^-^4	1	-0,5
40	4,36·10^-^4	1	-0,5
>40	4,36·10^-^4	1	-0,5

Punkt optymalny: x* = [4,36·10^-4, 1]

Wartość optymalna funkcji: f(x*) = -0.5

Wizualizacja rozwiÄ…zania:

Część analityczna:

f(x) = x₁² + x₁x₂ + 0.5x₂² - x₁ - x₂

II.2 Funkcje nie wypukłe

1. f(x) = x₁⁴ + x₂⁴ - 0.62x₁² - 0.62x₂² // funkcja z czterema minimami lokalnymi

Punkty optymalne: 1) x* = [- 0.55672, - 0.55672]

2) x* = [- 0.55672, 0.55672]

3) x* = [ 0.55672, - 0.55672]

4) x* = [ 0.55672, 0.55672]

Wartość optymalna funkcji: f(x*) = - 0.19219 (dla wszystkich punktów)

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Selekcja: turniejowa: twarda

Zakres zmiennych: x₁ = [-1, 1]

x₂ = [-1, 1]

Wizualizacja rozwiÄ…zania:

Poszukiwanie pierwszego punktu

Zakres zmiennych: x₁ = [-1, 0]

x₂ = [-1, 0]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 66 generacjach)

Punkt optymalny: x* = [-0.55678, -0.55677]

Wartość optymalna funkcji: f(x*) = -0.1922

Wizualizacja rozwiÄ…zania:

Poszukiwanie drugiego punktu

Zakres zmiennych: x₁ = [-1, 0]

x₂ = [0, 1]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 89 generacjach)

Punkt optymalny: x* = [-0.55678, 0.55678]

Wartość optymalna funkcji: f(x*) = -0.1922

Wizualizacja rozwiÄ…zania:

Poszukiwanie trzeciego punktu

Zakres zmiennych: x₁ = [0, 1]

x₂ = [-1, 0]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 94 generacjach)

Punkt optymalny: x* = [0.55678, -0.55678]

Wartość optymalna funkcji: f(x*) = -0.1922

Wizualizacja rozwiÄ…zania:

Poszukiwanie czwartego punktu

Zakres zmiennych: x₁ = [0, 1]

x₂ = [0, 1]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 117 generacjach)

Punkt optymalny: x* = [0.55678, 0.55678]

Wartość optymalna funkcji: f(x*) = -0.1922

Wizualizacja rozwiÄ…zania:

Część analityczna:

f(x) = x₁⁴ + x₂⁴ - 0.62x₁² - 0.62x₂²

2. f(x) = x₁⁴ + x₂⁴ - 2x₁²x₂ - 4x₁² + 3 // funkcja Engwall'a

Punkt optymalny: x* = [1.3090, 0.9498]

Wartość optymalna funkcji: f(x*) = -1.74109

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Selekcja: twarda

Zakres zmiennych: x₁ = [0, 2]

x₂ = [0, 2]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 129 generacjach)

Punkt optymalny: x* = [1.30735, 0.94897]

Wartość optymalna funkcji: f(x*) = -1.74107

Wizualizacja rozwiÄ…zania:

Część analityczna:

f(x) = x₁⁴ + x₂⁴ - 2x₁²x₂ - 4x₁² + 3

3. f(x) = (x₁² + x₂ - 11)² + (x₁ + x₂² - 7)² - 200 // funkcja Himmelblau'a

Punkty optymalne: cztery - brak danych

Wartość optymalna funkcji: f(x*) = - 200 (dla wszystkich punktów)

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Selekcja: twarda

Zakres zmiennych: x₁ = [-5, 5]

x₂ = [-5, 5]

Wizualizacja rozwiÄ…zania:

Poszukiwanie pierwszego punktu

Zakres zmiennych: x₁ = [-5, 0]

x₂ = [-5, 0]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 85 generacjach)

Punkt optymalny: x* = [-3.7792, -3.2832]

Wartość optymalna funkcji: f(x*) = -200

Wizualizacja rozwiÄ…zania:

Poszukiwanie drugiego punktu

Zakres zmiennych: x₁ = [-5, 0]

x₂ = [0, 5]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 88 generacjach)

Punkt optymalny: x* = [-2.8051, 3.1313]

Wartość optymalna funkcji: f(x*) = -200

Wizualizacja rozwiÄ…zania:

Poszukiwanie trzeciego punktu

Zakres zmiennych: x₁ = [0, 5]

x₂ = [-5, 0]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 91 generacjach)

Punkt optymalny: x* = [3.5844, -1.8481]

Wartość optymalna funkcji: f(x*) = -200

Wizualizacja rozwiÄ…zania:

Poszukiwanie czwartego punktu

Zakres zmiennych: x₁ = [0, 5]

x₂ = [0, 5]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 84 generacjach)

Punkt optymalny: x* = [3,2]

Wartość optymalna funkcji: f(x*) = -200

Wizualizacja rozwiÄ…zania:

Część analityczna:

f(x) = (x₁² + x₂ - 11)² + (x₁ + x₂² - 7)² - 200

4. f(x) = x₁² + x₁x₂ - 0.5x₂² - x₁ - x₂

Część programowa:

Ogólne założenia

Populacja początkowa: 40 osobników

Wybór początkowej populacji: losowy

Krzyżowanie: 60% (przez uśrednianie)

Mutacja: 12%

Selekcja: twarda

Pierwszy zakres

Zakres zmiennych: x₁ = [-10, 10]

x₂ = [-10, 10]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 91 generacjach)

Punkt optymalny: x* = [-4.5, 10]

Wartość optymalna funkcji: f(x*) = -80,25

Wizualizacja rozwiÄ…zania:

Drugi zakres

Zakres zmiennych: x₁ = [-100, 100]

x₂ = [-100, 100]

Kryterium stopu: brak postępu (optymalne rozwiązanie uzyskano po 91 generacjach)

Punkt optymalny: x* = [-52,784, 100]

Wartość optymalna funkcji: f(x*) = -7539,466

Wizualizacja rozwiÄ…zania:

Część analityczna:

f(x) = x₁² + x₁x₂ - 0.5x₂² - x₁ - x₂

III. Wnioski

Efektywność i dokładność obliczeniowa algorytmu genetycznego zależy głównie od prawidłowego doboru zakresu wartości zmiennych. Nieprawidłowy dobór obszaru powoduje błędne wskazania wartości optymalnej. W przypadku zbyt dużego obszaru algorytm może idealnie nie trafić w punkt optymalny, zbyt mały obszar powoduje nie znalezienie optymalnego rozwiązania (punkt optymalny będzie znajdował się na brzegach badanego obszaru).

Kolejnym istotnym problemem jest dobór algorytmu selekcji, ponieważ od nich zależy dokładność odszukanego optimum. Po zbadaniu efektywności trzech algorytmów selekcji: miękkiego, twardego oraz turniejowego stwierdzamy, że najefektywniejszym algorytmem jest algorytm selekcji twardej. Dobrym algorytmem jest również algorytm selekcji turniejowej, ponieważ w tych selekcjach przeżywają najlepiej przystosowane osobniki (niewłaściwy dobór parametrów selekcji w przypadku selekcji turniejowej może do wpadnięcia w minimum lokalne i nie znalezienia minimum globalnego). Z kolei w selekcji miękkiej w dużej populacji słabsze osobniki mogą przeżywać i rozmnażać się, lecz przeżywają lub rozmnażają się z mniejszym prawdopodobieństwem niż osobniki lepiej przystosowane, dlatego ten algorytm selekcji nie jest tak efektywny jak powyższe.

Ważnym parametrem jest rozmiar populacji. W zadaniach opracowywanych w tym ćwiczeniu optymalna liczba osobników w populacji powinna mieścić się w granicach 30 - 50. Na szybkość i efektywność algorytmu genetycznego poza algorytmem selekcji ma wpływ jakość osobników w początkowej populacji. A więc dobre losowanie (w przypadku zastosowania takiej metody wyboru początkowej populacji) ma bardzo duży wpływ na osiągnięcie optymalnego rozwiązania.

Decydujący wpływ na końcowe rozwiązanie ma kryterium stopu, czyli warunek decydujący o zatrzymaniu pracy algorytmu. Zdecydowanie najlepszym wyborem (naszym zdaniem) jest kryterium na brak postępu, ponieważ w miarę szybko znajduje optymalne rozwiązanie. W przypadku wyboru kryterium na liczbę generacji musimy orientować się jak dobrać tą liczbę. Zbyt mała liczba spowoduje, że algorytm nie dojdzie do rozwiązania optymalnego, natomiast zbyt duża liczba znacznie wydłuży czas wyszukiwania optimum.

Laboratorium	Technika optymalizacji
Autorzy: Dawid Tomasz (140517) Garbicz Marcin (140547) Kier.: EiT Spec.: ESA	Wrocław, dnia 6.11.2006 Prowadzący: Dr inż.. Ewa Szlachcic
Ćwiczenie IV Zadanie programowania nieliniowego bez ograniczeń	Algorytmy optymalizacji lokalnej i algorytmy optymalizacji globalnej

2

Może przydałby się ambitniejszy wstep?

Dla jednej funkcji (najlepiej jakiejś prostej np. 1, 2, 3) policzyć analityczne wartości optymalną i punkty, w których ono się znajduje.

Jak to zrobić?

1. Policzyć pierwsze pochodne cząstkowe po funkcji. Przyrównać je do zera - mamy punkty, w których znajduje się optimum.

2. Policzyć drugie pochodne cząstkowe. Robimy z nich macierz i obliczamy hesjan.

---