1. Prosty układ przełożenia z przekładnia zębata

SN - silnik napędowy (generuje moc)

MR - maszyna robocza (odbiera moc),Sp - sprzęgło

N- siły, M - momenty, n- częstotliwość?

u - przełożenie, ni- sprawność

2. Równania ewolwenty w układzie biegunowym

3. Zalety zarysu ewolwentowego:
- zęby kół można wykonać przy pomocy noża zębatkowego, który daje się łatwo i dokładnie wykonać,
- może być wykonany metodą obwiedniową, która jest tanią i dokładną metodą wykonania zębów kół,
- przy pomocy tego samego narzędzia można wykonać koła o różnych liczbach zębów, które dają się kojarzyć w dowolne pary, bez względu na liczbę zębów w kole,
- zmiany odległości osi kół nie wpływają na stałość przełożenia,
- kierunek działania siły międzyzębnej nie ulega podczas pracy zmianie,
- przy pomocy tego samego narzędzia można wykonać zęby korygowane.

Wady zarysu ewolwentowego:
- wysokie naciski pomiędzy zębami, wynikające z tego, że zęby stykają się wypukłościami.

4. Podstawowe parametry geometryczne koła o zębach prostych:

z - liczba zębów,
d - średnica podziałowa,
α - nominalny kąt przyporu na średnicy podziałowej,

da - średnica wierzchołkowa,
df - średnica stóp, podstaw,
s - grubość zęba.

ha-wysokość głowy zęba

hf- wysokość stopy zęba

5. Luzy w przekładni zębatej.

A) Luz wierzchołkowy c jest to najkrótsza odległość na prostej łączącej środki obu kół między wakcyn podstawy jednego koła a walcem wierzchołków koła drugiego. Luz ten jest niezbędny dla polepszenia warunków smarowania zębów( stanowi coś w rodzaju dodatkowego zbiorniczka oleju). c=c*m, gdzie c* - współczynnik luzu wierzchołkowego przyjmuje się go na poziomie 0,25:dopuszcza się 0,1<c*<0,4.

B) Luz boczny, który powinien zapewnić odpowiednią grubość filmu olejowego między współpracującymi bokami zębów. Wielkość tego luzu zależy również od stopnia rozszerzalności cieplnej materiału kół zębatych. Luz boczny może być wyrażony dwiema wielkościami: jako luz obwodowy lub międzyzębny normalny. Luz normalny j_{n ,}który przedstawia najkrótszą odległość między nie pracującymi bokami przy istnieniu kontaktu boków pracujących. W niektórych mechanizmach luz międzyzębny normalny jest niepożądany. Luz obwodowy j_t przedstawia długość łuku okręgu tocznego, o który można obrócić koło, aby doprowadzić boki nie pracujące do styku, podczas gdy koło współpracujące jest unieruchomione.

6. Podcinanie stopy zęba.

Podczas nacinania zębów nożem zębatkowym według metody obwiedniowej może nastąpić zjawisko podcinania stopy zęba koła przez zęby narzędzia. Przy dużej liczbie zębów w kole przejście ewolwenty w okolicy okręgu zasadniczego w krzywą ograniczającą stopę zęba następuje w miejscu, gdzie styczne do obu krzywych wzajemnie się pokrywają. Przy małej liczbie zębów w kole część ewolwenty powyżej okręgu zasadniczego zostanie ścięta.

By uniknąć podcinania stopy zęba należy przyjmować liczbę zębów:

7. Czołowa liczba przyporu

Dla zapewnienia ciągłości pracy kół zębatych, ząb następny musi wejść w zazębienie zanim poprzedni wyjdzie z zazębienia. W przypadku zębów prostych jest konieczne, aby odcinek przyporu „g” był większy od odległości pomiędzy zębami mierzonej wzdłuż tego odcinka a równej podziałce zasadniczej. Wymaga się, aby odcinek przyporu był o 20% większy od podziałki. Stosunek tych odcinków nazywamy wskaźnikiem przyporu czołowego lub czołową liczba przyporu.

8. Korekcja zazębienia (wady, zalety, wpływ na

kształt zęba).

Korekcja ujemna:

-pogarsza warunki pracy,

-używana jest tylko dla uzyskania potrzebnej odległości osi w kołach o dużej liczbie zębów.

Korekcja dodatnia jest ograniczona zaostrzeniem zęba.

-Z praktyki wiadomo, że grubość zęba na kole wierzchołkowym nie może nie może być mniejsza niż 0,4 m, ze względu na luz.

Rodzaje korekcji zazębienia:

-bez przesunięcia (zazębienie niekorygowane)

x1=x2=0

-równej sumie przesunięć (korekcja P-0)

x1=-x2 albo x1+x2=0

-dodatniej lub ujemnej sumie przesunięć
(korekcja P) x1+x2≠0

Stosując korekcję P-0 zachowuje się taką samą odległość osi i ten sam kąt zarysu, czyli średnica toczna pokrywa się z podziałową. Dodatnie przesunięcie występuje dla zębnika, co pozwala na uniknięcie podcinania, nadając zębom małego koła korzystne kształty z punktu widzenia wytrzymałości zmęczeniowej. Dla dużego koła występuje ujemne przesunięcie zarysu ma mały wpływ na jego kształt.

Dla korekcji P współczynnik x₁ i x₂ dobiera się oddzielnie, aby w optymalny sposób spełnione były warunki wytrzymałościowe kół.

Korekcji P wymaga zmiany odległości osi, natomiast przy korekcji P-0 odległość osi kół nie ulega zmianie.

9. Rozkład sil w zazębieniu kół o zębach skośnych.

10. Obciążenie jednostkowe Q, Qu:

Bardzo praktyczną wielkością w obliczeniach wytrzymałościowych okazał się wielkość nazywana obciążeniem jednostkowym Q

W obliczeniach nacisków międzyrębnych występuje ona łącznie z funkcją przełożenia w postaci

11. Wpływ przeciążeń zewnętrznych Kp:

Współczynnik Kp jest liczbą, przez którą należy pomnożyć moment nominalny, aby otrzymać moment obliczeniowy, który działając stale, daje taki sam stopień niezawodności działania przekładni jak rzeczywiście działający, zmienny w czasie moment obrotowy.

W wielu przypadkach zmienia się w czasie nie tylko moment obrotowy, ale także prędkość obrotowa.

12. Wpływ obciążeń wewnętrznych Kd

Przyczyny powstawania drgań, czyli wymuszenia, mogą pochodzić ze źródeł zewnętrznych, np. od silnika lub maszyny roboczej, a także ze źródeł wewnętrznych.

Natomiast źródła wewnętrzne mają znacznie wyższą częstotliwość pobudzania i dlatego mają większe znaczenie w dynamice przekładni.

Zwiększonym wahaniom bryły towarzyszą zwiększone ugięcia sprężyn, tym samym zwiększone w nich naprężenia, które trzeba uwzględnić za pomocą współczynnika Kd.

14. Nierównomierne obciążenie na szerokości kół:

Kr, Krt, Ks

Nierównomierny rozkład obciążenia na szerokości koła jest wywołany trzema przyczynami:

1) Wadliwa obróbka mechaniczna prowadzi między innymi do powstania następujących odchyłek mających bezpośredni wpływ na ślad przylegania: nierównoległość osi, wichrowatość osi i błąd

kierunku linii zęba

Skutki odchyłek wykonawczych zostały ujęte za pomocą współczynnika Kr.

2) Często się zdarza, że koła wykazujące prawidłowy ślad przylegania zębów podczas technicznego odbioru bez obciążenia, wykazują w okresie normalnej pracy

ślad nieprawidłowy, również najczęściej jednostronny

3) W kołach o zębach prostych ząb wchodzi w zazębienie jednocześnie na całej szerokości koła

15. Wyznaczanie naprężeń u podstawy zęba:

Wyznaczenie skutecznej wartości naprężeń np. za pomocą wzoru

gdzie: α - współczynniki koncentracji naprężeń odpowiednio: gnących, ściskających (+) lub rozciągających(-) i tnących

Naprężenie obliczeniowe u podstawy zęba:

Gdzie:

P - obciążenie

m - moduł

b - szerokość koła

q - współczynnik kształtu zęba (z wykresu bądź wyliczony)

Metody numeryczne:

1. Metoda elementów skończonych MES wymaga podziału zęba na przynajmniej 250 elementów i rozwiązania od 500 do 1500 równań liniowych.

2. Metoda elementów brzegowych MEB wymaga wyznaczenia, na obrysie zęba, przynajmniej 50 punktów i rozwiązania 100 równań liniowych

3. Metoda odwzorowań wiernokątnych daje zadowalające rezultaty już przy założeniu tylko 4 punktów na zarysie stopy zęba i rozwiązania 8 równań, tym razem jednak nieliniowych, co stwarza nowe problemy obliczeniowe.

16. Wytrzymałość zmęczeniowa zęba.

Badania wytrzymałości zęba na złamanie prowadzi się zwykle na specjalnych stanowiskach mocy krążącej. Zęby mają zwykle moduł m=3 [mm], wykonane są w 6 klasie dokładności, a promień krzywizny u podstawy zęba
wynosi ok. 0,2 m. Ustalenie wartości Z
wymaga przyjęcia konkretnej metody obliczania, ponieważ konieczne jest ustalenie szeregu współczynników

Wpływ wielkości zęba na jego wytrzymałość

W przypadku założenia płaskiego stanu naprężeń współczynnik wielkości zęba można przedstawić w postaci zależności:

- W przypadku ogólnym współczynnik uzależnia się dla materiałów plastycznych od przekroju zęba bm , a dla materiałów kruchych od objętości bm², na postawie dotychczasowych wyrywkowych doświadczeń przyjęto:

a) dla kół stalowych:

b) dla kół kruchych:

Wpływ karbu u podstawy zęba

Zwykle dobiera się tak narzędzia, aby uzyskać wartość
/m=0,2. W ten sposób określona na podstawie badań wytrzymałość zęba uwzględnia w znacznym już stopniu spiętrzenie naprężeń, wywołane działaniem karbu. W przypadkach, gdy projektowane koła będą miały istotnie różny zredukowany promień karbu
/m wprowadza się poprawkę w postaci współczynnika y
, którego wartość dla przykładu
/m
=0,2 można z dobrym przybliżeniem obliczyć za pomocą równania:

Mikronierówności stopy zęba powstałe w procesie nacinania zębów są powodem dodatkowych naprężeń

17. Współczynniki bezpieczeństwa na złamanie.

a) dla małego koła można wprowadzić jeden współczynnik Y_e1 = q₁y_k1

b) dla dużego koła można wprowadzić jeden współczynnik Y_e2 = q₂y_k2

18. Współczynnik bezpieczeństwa na naciski:

W punkcie tocznym C zachodzą następujące zależności:

ρ₁ = 0,5dw₁sinα_w

ρ₂ = 0,5dw₂sinα_w

Maksymalny nacisk w punkcie tocznym C:

Wartość średniego nacisku w punkcie C:

k_C = y_CQ_U

19. Zależności między współczynnikami bezpieczeństwa na naciski i złamanie

Dla zębów prostych w przeciętnych warunkach wykonania:

Stosunek współczynników bezpieczeństwa zależy od:

• Właściwości mechanicznych materiału wyrażających się stosunkiem wytrzymałości zmęczeniowej na złamanie do wytrzymałości na naciski Z_z1: k_z1

• Liczby zębów z₁ od której zależą współczynniki ujęte w drugi człon równania

• Przełożenia u

20. Rozkład przełożenia na poszczególne stopnie

Optymalną liczbę stopni oraz optymalny rozkład przełożenia na poszczególne stopnie określa konstruktor. Wybór najlepszego rozwiązania zależy od spełnienia warunków:

• ze względów wytrzymałościowych korzystnie jest, aby liczby zębów współpracujących kół nie miały wspólnych podzielników (były liczbami pierwszymi)

• całkowity koszt produkcji przekładni powinien być możliwie mały,

• całkowita masa przekładni, a zwłaszcza elementów wirujących, powinna być możliwie mała,

• całkowity moment bezwładności elementów wirujących powinien być jak najmniejszy,

• duże koła poszczególnych stopni powinny mieć w przybliżeniu równe średnice, aby jednakowo zanurzały się w oleju,

• całkowita długość przekładni, lub długość zajęta przez elementy wirujące powinna być mała.

21.Dobór liczby zębów zębnika z1

Liczba zębów koła z2 wynika w szczególności z obliczonej liczby zębów zębnika z1 oraz obranego przełożenia u1 rozpatrywanego stopnia. Dla zwiększenia wytrzymałości zęba na naciski korzystnie jest tak dobrać liczbę zębów z2 aby była bliska iloczynowi z1u1 i była przy tym liczbą pierwszą względem z1 tj. aby liczby z1 oraz z2 nie miały wspólnych podzielników. W ten sposób ustala się ostatecznie wartość przełożenia danego stopnia u = z2 / z1.

W przekładniach wykonanych w najniższych klasach dokładności, np. w przypadku zębów nie obrabianych mechanicznie, lepiej jest tak dobierać liczby zębów, aby miały jak najwięcej wspólnych podzielników, tj. aby przełożenie u (jeżeli to tylko możliwe) było liczbą całkowitą. Wtedy bowiem często następuje współpraca tych samych zębów, co ułatwia ich dotarcie się i powoduje znaczne zmniejszenie błędów kinematycznych. Natomiast w przekładniach precyzyjnie wykonanych korzystniej jest, gdy ewentualne nierówności powierzchni spotykają się ze sobą jak najrzadziej, co przedłuża ich czas pracy

22. Dobór względnej szerokości zębnika.

Wykonuje się na podstawie następującego stosunku:

ၫ = b/d1 - (kappa) względna szerokość koła.

d - średnica podziałowa koła, b - szerokość zębnika

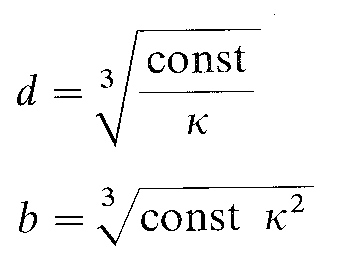
Im większe jest ၫ, tym mniejsze średnice kół i tym mniejsza całkowita długość przekładni, a także tym mniejszy moment bezwładności. Obliczenie szerokości koła b.

24. Wady i zalety przekładni obiegowych:

Zalety:

-mniejsze gabaryty

-mniejsza masa

-większa sprawność

-przekładnie obiegowe mają zwykle większą liczbę -stopni swobody, co umożliwia:

-sumowanie momentów i mocy pochodzących z

-kilku napędów (przekładnie sumujące)

-rozdział momentów i mocy na kilka odbiorników Wady:

-wyższe koszty wytwarzania

25.BUDOWA PROSTEJ PRZEKLADNI OBIEGOWEJ

Prosta przekładnia obiegowa składa się z następujących elementów:

- koła centralnego 1 osadzonego na wale 1

- koła centralnego 2 osadzonego na wale 2

- jarzma kół obiegowych osadzonego na wale h

- trzech kół obiegowych (satelitów) p, ułożyskowanych w jarzmie h i równomiernie rozmieszczonych na obwodzie, sprzęgającym koło 1 z kołem 2.

Przekładania obiegowa wykonana jest ze stali utwardzonej, z wyjątkiem koła wewnętrznego uzębionego, wykonanego ze stali ulepszanej cieplnie. Zwykle przekładnie wykonane są też ze stali ulepszanej.

26. DEFINICJA PRZELOZENIA BAZOWEGO, SPRAWNOSCI BAZOWEJ

Przełożenie bazowe określające stosunek prędkości obrotowych wałów n₁,n₂ przy nieruchomym jarzmie (n_h=0)

Sprawność bazowa będąca stosunkiem mocy wyjściowej N₂ ze znakiem ujemnym do mocy wejściowej N lub wartością bezwzględnej tego stosunku przy nieruchomym jarzmie (n_h=0)

Bardzo istotną cechą przekładni obiegowych jest znak i₀, określający kierunek obrotów kół centralnych w przypadku nieruchomego jarzma (n_h=0).Jeżeli kierunki obrotów obu kół centralnych są jednakowe, to przełożenie bazowe jest dodatnie (i₀>0), natomiast gdy kierunki są przeciwne, przełożenie bazowe jest ujemne (i₀<0).

27. Analityczny sposób wyznaczania prędkości

obrotowych, przełożenia i zależności między

nimi.

W metodzie analitycznej rozpatruje się przypadek, w którym obserwator porusza się wraz z jarzmem i określa liczby obrotów kół względem jarzma. Dla obserwatora osie kół są w stałym względem niego i jarzma położeniu wobec tego przekładnie uważamy za zwykłą o stałych osiach. Oznaczając bezwzględne prędkości obrotowe symbolami n₁ i n₂ oraz n_h, prędkości obrotowe względem jarzma (obserwatora) określamy jako (n₁-n_h) oraz (n₂-n_h), zatem przełożenie bazowe wynosi

i₁₂ - oznacza przełożenie miedzy wałem 1 i 2 w przypadku gdy jeden wał jest unieruchomiony

j - oznacza przełożenie gdy wszystkie 3 wały są ruchome

Z powyższego równania:

możemy wyznaczyć przełożenia dla różnych kombinacji obrotów, między innymi w następujących szczególnych przypadkach

1. zahamowanie jarzma (n_h=0)
lub

2. jeżeli n₂=0 n₁=(1-i₀)n_k lub

3. jeżeli n₁=0
lub

W przypadku, gdy wszystkie wały są ruchome muszą być ustalone dwie prędkości obrotowe np. n₁i n₂ umożliwia to wyznaczenie trzeciej wielkości, np. n_h.

Równanie n₁-n₂*i₀-n_h(1-i₀)=0 sprowadzamy do bezwymiarowej postaci tj. do związku pomiędzy przełożeniami, będącymi stosunkami prędkości obrotowych poszczególnych wałów przkładni:

Otrzymujemy między innymi:

oraz

28. Obliczanie momentów w prostej przekładni

Zgodnie z warunkami równowagi suma momentów działających na trzy wały przekładni musi spełniać równanie M₁+M₂+M_n=0

Z równania tego wynika, że jeden wał obciążony jest momentem o przeciwnym znaku niż dwa pozostałe wały. Wał ten nazywa się wałem sumującym, ponieważ obciążony jest momentem równym bezwzględnej wartości sumy pozostałych dwóch momentów.

W przekładni o bazowym położeniu ujemnym (io<0) sumaryczny moment występuje zawsze na wale jarzma, co łatwo zauważyć, jeżeli przyjmuje się dwie siły międzyzębne na obwodzie koła obiegowego, których wypadkowa działająca na oś koła obiegowego, a tym samym na jarzmo, wytwarza moment sumaryczny. Oznacza to jednocześnie ze wały kół centralnych są wałami różnicowymi.

W przekładni o bazowym położeniu dodatnim (io>0) wał jarzma jest zawsze wałem różnicowym, natomiast wał koła centralnego o mniejszej prędkości obrotowej tj. większym momencie obrotowym, jest wałem sumującym. Wynika stąd, że o umiejscowieniu wału sumującego decyduje przełożenie bazowe. W przypadku, gdy jest ono większe od 1, większy moment występuje na wale zdawczym, który jest wałem sumującym.

Znaki momentów określa się następująco: moment, który działa na wał w kierunku zgodnym z dodatnim kierunkiem prędkości, ma znak dodatni, natomiast gdy moment działa w przeciwną stronę, ma on znak ujemny.

29. Obliczanie mocy:

4 warianty wyznaczania mocy:

1. nieruchome jarzmo - przekładnia o osiach stałych, moc N_z

2. koło wewnętrzne unieruchomione - moc N=N_z+N_s

N_z=M₁(n₁-n₂)>0 moc przenoszona przez uzębienie

N_s=M₁ n_h >0 moc przenoszona przez sprzęgło

3. Wszystkie 3 elementy mają równe prędkości obrotowe - sprzęgło zębate

N=N_s=M₁ n_h

4. Wszystkie elementy są w ruchu ale prędkość obrotowa jarzma jest większa

N_z=M₁(n₁-n_h)<0

N_s=M₁ n_n >0

30. Warunek poprawnego doboru liczby zębów

-liczba zębów w kołach powinna być bliska optymalnej, tj. zapewniającej odpowiedni stosunek współczynników bezpieczeństwa na złamanie i naciski,

-koła obiegowe nie mogą dotykać się obwodami, co ogranicza ich maksymalną średnicę, a tym samym i ekstremalną wartość przełożenia,

-montaż musi umożliwiać usytuowanie koła centralnego pomiędzy kołami obiegowymi o ustalonym już wzajemnym położeniu, warunek ten wyznacza związek pomiędzy liczbą zębów a liczbą kół obiegowych.

Dodatkowo wskazany jest taki wybór liczby zębów, aby zapewnić optymalne warunki dynamiczne związane z chwilą wejścia w przypór poszczególnych par zębów.

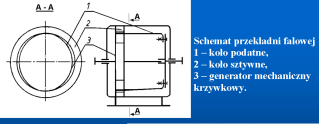
31. Budowa przekładni falowej:

---