Kształt Ziemi

O tym , że Ziemia nie jest płaska wiedziano już w starożytności. Dowody na przedstawił Arystoteles w IV w pne, a Erastotenes około 230 r pne obliczył długość promienia Ziemi.

Zauważył on, że 22 czerwca w południe nawet najgłębsze studnie w Asuanie są oświetlone aż do dna- promienie słońca padają dokładnie pionowo. Kiedy nadarzyła się okazja, w leżącej kilkaset kilometrów na północ Aleksandrii zmierzył tego samego dnia w południe kąt między pionem a kierunkiem padania promieni słonecznych - był to również kąt między promieniami Ziemi przechodzącymi przez Aleksandrię i Asuan. Znając odległość (l) między Tymi miastami obliczył promień Ziemi ze wzoru:

R=(l * 360^o)/(* )

Wynik, który otrzymał różnił się od rzeczywistego jedynie o 100 kilometrów, a wynikał głównie z niedoskonałości instrumentów pomiarowych. Chwała Erastotenesowi. Panowie, czapki z głów! W 1686 Francuz Jean Richer odkrył spłaszczenie Ziemi przy biegunach, a Izaak Newton określił bryłę Ziemi, jako elipsoidę obrotową, obliczył spłaszczenie Ziemi i stwierdził, że jej kształt jest wynikiem ruchu wirowego planety.

Niemiec Johann Listing w XiX wieku wprowadził pojęcie geoidy - bryły , która powstałaby, gdyby poziom swobodnej powierzchni mórz przedłużyć pod lądami. To pojęcie dotyczące kształtu Ziemi obowiązuje do dziś.

Bryłę Ziemi określa się również, jako elipsoidę trójosiową - to znaczy bryłę, która w trzech przekrojach prostopadłych do siebie daje trzy różne elipsy. Oznacza to, że promień równikowy Ziemi nie jest identyczny we wszystkich kierunkach, ale zmienia długość (w granicach 200 metrów).

WYMIARY ZIEMI:

promień równikowy	6 378,24 km
promień biegunowy	6 356,86 km
spłaszczenie	21,38 km
objętość	1 083 mld km^3
powierzchnia	510 mln km^2
masa	5 977 tryl ton

Ruch obrotowy to ruch, jaki wykonuje Ziemia obracając się wokół własnej osi. Ziemia obraca się wokół własnej osi z zachodu na wschód, a więc patrząc od strony bieguna północnego jest to ruch lewoskrętny. Pełny obrót trwa 23 godziny 56 minuty i 4 sekundy. Następstwami ruchu obrotowego są: zjawisko dnia i nocy, pozorny ruch sklepienia niebieskiego (ruch Słońca i gwiazd nad horyzontem), możliwość pomiaru czasu (doba).
Dowody świadczące o ruchu obrotowym Ziemi: odchylenie ciał swobodnie spadających na wschód i zmiana kierunku płaszczyzny wahań wahadła Foucaulta oraz spłaszczenie Ziemi i siła Coriolisa.

Osią ziemi jest średnica, wokół której obraca się Ziemia, krańce owej osi to bieguny: północny i południowy. Zerowy równoleżnik, czyli równik powstaje poprzez przecięcie ziemi płaszczyzną prostopadłą do osi ziemi i przechodzącą przez jej środek. Równik dzieli też kulę ziemską na dwie półkule: północną i południową.

Równoleżniki to okręgi o promieniach mniejszych niż promień Ziemi i równoległe do równika, ich płaszczyzny nie przechodzą przez środek Ziemi. Południki to okręgi o promieniach równych promieniowi Ziemi i przechodzące przez bieguny północny i południowy, ich płaszczyzny przechodzą przez środek Ziemi. Południk zerowy przechodzi przez londyńską dzielnicę Greenwich i dzieli kulę ziemską na dwie półkule: wschodnią i zachodnią.

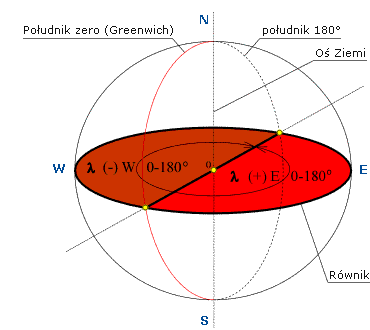
Długość i szerokość geograficzna

Długość geograficzna λ (górna i dolna podziałka na mapie)
Jest to miara kątowa między południkiem zerowym (Greenwich) a dowolnym innym południkiem. Długość geograficzną mierzy się od południka zerowego na wschód lub zachód. Symbolem długości geograficznej jest litera λ.
Wszystkie punkty na wschód od południka Greenwich (od 0 do 180°) mają długość wschodnią, więc przy zapisie współrzędnych dodaje się znak [+] lub E i zapisuje tak:
λ = +012° 47,3'
lub tak:
λ = 012° 47,3' E
Wszystkie punkty na zachód od południka Greenwich (od 0 do 180°) mają długość zachodnią, przy zapisie współrzędnych dodaje się znak [-] lub W i zapisuje się tak:
λ = -012° 47,3'
lub tak:
λ = 012° 47,3' W

Południk 180° jest międzynarodową linią zmiany daty

 

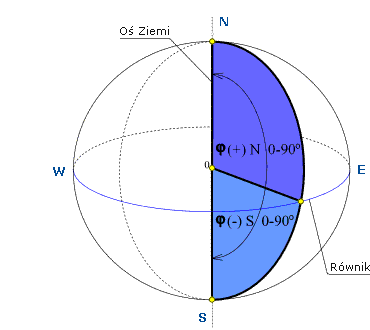
Szerokość geograficzna φ (boczne, prawa i lewa podziałka na mapie)
Jest to miara kątowa między równikiem a dowolnym innym równoleżnikiem. Szerokość geograficzną mierzy się od równika na północ lub południe. Symbolem szerokości geograficznej jest litera φ (fi).
Wszystkie punkty na północ od równika (od 0 do 90°) mają szerokość północną, więc przy zapisie współrzędnych dodaje się znak [+] lub N i zapisuje tak:
φ = +55° 32,5'
lub tak:
φ = 55° 32,5' N
Wszystkie punkty na południe od równika (od 0 do 90°) mają szerokość południową, przy zapisie współrzędnych dodaje się znak [-] lub S i zapisuje się tak:
φ = -55° 32,5'
lub tak:
φ = 55° 32,5' S

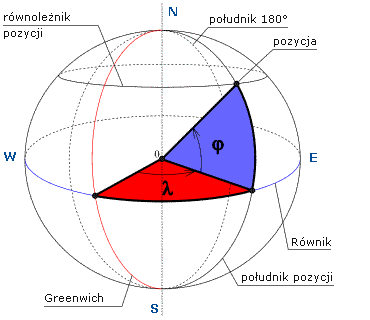
Tak więc położenie statku na morzu określają dwie współrzędne: długość i szerokość geograficzna. W praktyce współrzędne pozycji najczęściej zapisuje się w ten sposób:

φ = 55° 32,5' N ; λ = 012° 47,3' E

Długość i szerokość geograficzną mierzy się w stopniach, minutach i sekundach, gdzie :

1° = 60'
1' = 60''

Różnica szerokości i długości geograficznej

Różnica szerokości geograficznej dwóch punktów (A, B), jest różnicą odległości kątowej równoleżników tych punktów od równika.
Różnica długości geograficznej dwóch punktów (C, D), jest różnicą odległości kątowej południków tych punktów od południka zerowego (Gr).

rφ = φ_B - φ_A
rλ = λ_B - λ_A

rφ    N (+)		rλ    E (+)
S (-)		W (-)

Uwaga: Obowiązkowo stosować znaki, jest to niezbędne przy późniejszych obliczeniach loksodromy. Znaki przy rφ i rλ wskażą nam kierunek przemieszczania się statku.

Pozycja 1	φA = 20° 00' N
	λA = 010° 00' E
	φB = 40° 00' N
	λB = 010° 00' E
	rφ = (+40° 00') - (+20° 00') = (+20° 00')
	rλ = (+010° 00') - (+010° 00') = (±00° 00')

 

Pozycja 2	φC = 10° 00' N
	λC = 020° 00' E
	φD = 10° 00' N
	λD = 050° 00' E
	rφ = (+10° 00') - (+10° 00') = (±00° 00')
	rλ = (+050° 00') - (+020° 00') = (+030° 00')

Powyższe przykłady są przykładami prostymi, przedstawionymi na mapie Merkatora (patrz rysunek powyżej). W praktyce mamy do czynienia z żeglugą loksodromiczną, czyli od pozycji do pozycji o różnych współrzędnych geograficznych.

Przykład:	φA = 52° 34'5 N
	λA = 018° 22'0 E
	φB = 56° 33'9 N
	λB = 011° 29'2 E
	rφ = (+56° 33'9) - (+52° 34'5) = (+3° 59'4)
	rλ = (+011° 29'2) - (+018° 22'0) = (-006° 52'8)

Widzimy tutaj znaki; przy rφ (+), a przy rλ (-), czyli już wiemy, że kurs z punktu A do punktu B będzie w ćwiartce NW.

Możemy mieć i taką sytuację.

Przykład:	φA = 54° 32'0 N
	λA = 012° 15'0 W
	φB = 36° 49'0 S
	λB = 176° 59'0 E
	rφ = (-36° 49'0) - (+54° 32'0) = (-91° 21'0)
	rλ = (+176° 59'0) - (-012° 15'0) = (+189° 14'0)
	360° - 189° 14'0 = (-170° 46'0)

Jeżeli rλ wyjdzie większa niż 180°, wówczas wynik odejmujemy od 360° i zmieniamy znak na przeciwny.

Uwaga: Po obliczeniu różnicy szerokości i długości geograficznej stopnie należy zamienić na minuty, stosując odpowiedni znak. Jest to przydatne do późniejszych obliczeń, kiedy te wartości podstawiamy do wzorów. Należy to robić po każdym obliczeniu. I tak, jeżeli przykładowo obliczyliśmy:

rφ = (+12° 34'0) , to od razu za nawiasem zapisujemy (+754'0)
rλ = (- 6° 44'0) = (- 404'0)

Takie wartości wprowadzamy do wzorów, czyli dalszych obliczeń.

Horyzont i widnokrąg

Horyzont obserwatora - jest to płaszczyzna oddalona od powierzchni Ziemi o tzw. wysokość oczną, (czyli odległość równą wzniesieniu oczu obserwatora nad powierzchnię Ziemi) i prostopadła do linii pionu przechodzącej przez miejsce obserwatora i środek Ziemi.

Horyzont geometryczny (zwany też prawdziwy) - to płaszczyzna stożka wyprowadzonego na wysokości oka obserwatora i opartego o kształt Ziemi. Punkt styczności z Ziemią nazywamy jest widnokręgiem.

Horyzont astronomiczny - to płaszczyzna równoległa do horyzontu obserwatora i przechodząca przez środek Ziemi.

Zasięg wzroku obserwatora jest ograniczony linią widnokręgu i zależy od wysokości ocznej.

Termin horyzont często jest mylony z terminem widnokrąg. Jeżeli mówimy, że coś widać na horyzoncie, to tak naprawdę mamy na myśli widnokrąg.

Znając wysokość wzniesienia oczu obserwatora (h) można łatwo obliczyć odległość do widnokręgu, co w pewnych sytuacjach może być istotne (np. ocena dystansu dzielącego jacht od brzegu). Odległość liczymy ze wzoru.

Wzór możemy wykorzystać i obliczyć odległość do obiektu o znanej wysokości (np. światła latarni morskiej) wykorzystując moment, w którym światło kryje się za widnokręgiem. Moment taki najlepiej uchwycić, kiedy światło jest widoczne dla stojącego na pokładzie obserwatora a niewidoczne dla obserwatora siedzącego.

Refrakcja ziemska - średnia odległość widnokręgu

Refrakcja ziemska jest to załamanie się promieni świetlnych w otaczających ziemię powłokach powietrza. Na skutek różnej gęstości warstw powietrza, promienie świetlne biegną po krzywej wygiętej ku górze. Taką refrakcję nazywamy średnią refrakcją ziemską. Na skutek tego obserwator widzi nie do punktu, W' lecz do punktu W''.
Refrakcja powiększa odległość widnokręgu o 1/13. Jest to (około) 8% odległości widnokręgu, czyli średnia odległość widnokręgu jest to odległość widnokręgu powiększona o 1/13.

Odległość do widnokręgu, jest to mierzona w milach morskich [Mm], odległość od obserwatora do punktu, w którym promień oczny jest styczny do powierzchni kuli ziemskiej.
Obniżenie widnokręgu (głębokość widnokręgu) (Ko) jest to kąt zawarty między horyzontem obserwatora, a linią przechodzącą przez oczy obserwatora i styczną do powierzchni kuli ziemskiej.

h - wysokość oka obserwatora
Ho - horyzont obserwatora
Ko - obniżenie widnokręgu
K - średnie obniżenie widnokręgu
W' - odległość widnokręgu
W'' - średnia odległość widnokręgu

Wyprowadzenie wzoru

Wykorzystując twierdzenie Pitagorasa dla trójkąta prostokątnego OBC można wyprowadzić wzór na odległość do widnokręgu.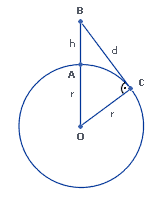

AB = h (wysokosc oczu obserwatora nad poziomem morza w metrach)
OA = OC = R (promień Ziemi)
BC = d (szukana odległość do widnokręgu obserwatora)
BO = h + R
CO = R
więc
BO² = BC² + CO²
(R + h)² = d² + R²

d² = (R + h)² - R² = R² + 2Rh + h² - R²  (upraszczamy)





Ze względu na minimalną wartość do promienia Ziemi "h" pomijamy w wyrażeniu (h+2R), wówczas otrzymamy:


obliczamy w Mm wyrażenie   


Podstawiamy średnią wartość promienia kuli ziemskiej R = 6370 x 10³ m i dzielimy wynik przez 1852 m
w celu uzyskania odległości w milach morskich (Mm)

tak, więc    


Niejednorodna gęstość atmosfery powoduje, że promienie świetlne ulegają pewnemu załamaniu, więc odległość do widnokręgu będzie nieco większa. Ostatecznie wskutek refrakcji, średnia odległość do widnokręgu jest powiększona o 1/13.


Wysokość oka obserwatora podawana jest w metrach lub stopach, wówczas mamy dwa wzory:

Kształt i geometria Ziemi.

Na kształt Ziemi wpływa wiele czynników: jej ruch obrotowy i obiegowy, cieplny i grawitacyjny wpływ ciał niebieskich, własności fizyczne litosfery i hydrosfery i wiele innych. Przy rozpatrywaniu kształtu Ziemi rozróżnia się jej powierzchnię fizyczną i powierzchnię poziomu odniesienia. Za fizyczną powierzchnię Ziemi przyjmuje się jej rzeczywistą powierzchnię ze wszystkimi szczegółami lądów oraz powierzchnią mórz i oceanów. Powierzchnią poziomu odniesienia nazywamy niezaburzoną powierzchnię mórz i oceanów oraz jej przedłużenie pod powierzchnią lądów.
Powierzchnia wód wyznaczająca poziom odniesienia podlega tylko działaniu siły grawitacji ziemskiej, jest, zatem w każdym punkcie prostopadła do kierunku siły ciężkości. Wpływ innych sił, realnie oddziaływujących na morza i oceany (zjawiska atmosferyczne i grawitacja ciał niebieskich), jest uśredniany. W praktyce powierzchnię poziomu odniesienia określa średni poziom morza (mean sea level - MSL).

Bryła geometryczna wyznaczona powierzchnią poziomu odniesienia nazywa się geoidą. Geoida jest bryłą nieregularną, trudną do opisania za pomocą wzorów matematycznych. Przybliżony matematyczny model geoidy nazywamy datum geodezyjnym (World Geodetic System - WGS).
Wystarczającym praktycznym przybliżeniem geoidy jest elipsoidą obrotową. Elipsoidę o wymiarach najbardziej zbliżonych do wymiarów geoidy nazywa się elipsoidą ziemską. Środek elipsoidy ziemskiej pokrywa się ze środkiem ciężkości Ziemi. Krótsza oś elipsoidy pokrywa się z osią obrotu Ziemi. Promień najdłuższego obwodu elipsoidy ziemskiej liczy sobie 6378,245 km, a półoś 6356,863 km.
Na ogół powierzchnia geoidy przebiega na obszarach lądowych powyżej powierzchni elipsoidy ziemskiej, a na obszarach mórz i oceanów poniżej tej powierzchni. Odchylenia te nie przekraczają 150 m; średnio wynoszą około 50 m.

Definicje układów współrzędnych opierają się na matematyczno-fizycznych modelach Ziemi (określanych rezolucjami Międzynarodowej Unii Geodezji i Geofizyki oraz Międzynarodowej Asocjacji Geodezji), metryce i standaryzacji przestrzeni geodezyjnej. Stosowane obecnie modele to GRS'80 (ang. Geodetic Reference System'80) oraz zmodyfikowany później WGS'84 (ang. World Geodetic System' 84). Model Ziemi obejmuje zbiór parametrów geometryczno - fizycznych. Elementem geometrycznym jest elipsoida odniesienia, która przyjmuje nazwę modelu. Elipsoidy GRS'80 i WGS'84 nie różnią się istotnie parametrami geometrycznymi (różnica półosi b nie przekracza 0.1mm), dlatego w odwzorowaniach kartograficznych nie dokonuje się w zasadzie rozróżniania elipsoid. WGS'84 jest aktualnie przyjętą elipsoidą globalnego, satelitarnego systemu obserwacyjno - pozycyjnego GPS (ang. Global Positioning System). Elipsoidę GRS'80 stosuje się formalnie w Polsce w odwzorowaniach kartograficznych, nowych państwowych układów współrzędnych 1992, 2000.

---