Nr ćwiczenia: 9	Temat ćwiczenia: Współczynnik załamania światła dla ciał stałych	Ocenia z teorii:
Nr zespołu: 6	Imię i nazwisko: Michał Koczur	Ocena z zal. ćwiczenia:
Data: 19.03.2007	wydział: EAIiE rok: I grupa: 2	Uwagi:

I. Cel ćwiczenia

Wyznaczenie współczynnika załamania ciał stałych za pomocą mikroskopu.

II. Wymagane wiadomości teoretyczne

• Definicja współczynnika załamania - stosunek sinusa kąta padania (α) do sinusa kąta załamania (β) lub stosunek szybkości światła w ośrodkach

• Zasada Huygensa - każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane są falami cząstkowymi

i interferują ze sobą. Wypadkową powierzchnię falową tworzy powierzchnia styczna do wszystkich powierzchni fal cząstkowych i ją właśnie obserwujemy w ośrodku.

• Prawo odbicia i załamania światła

• kąt padania światła na granicę dwóch ośrodków o różnej gęstości jest równy kątowi odbicia

• promień padający, odbity, załamany oraz normalna leżą w jednej płaszczyźnie

• stosunek sinusa kąta padania do sinusa kąta załamania jest dla danych dwóch ośrodków wielkością stałą, nazywaną współczynnikiem załamania tych ośrodków

• kąt graniczny - kąt padania przy którym kąt załamania wynosi 90^o

• Całkowite wewnętrzne odbicie - zjawisko zachodzące w przypadku, gdy kąt padania jest większy od kąta granicznego, promień padający na granicę dwóch ośrodków ulega całkowitemu odbiciu

• Dyspersja - zależność współczynnika załamania ośrodka (n) od długości fali

• Dyspersja normalna - wraz z maleniem długości fali
  rośnie współczynnik załamania światła

• Dyspersja anomalna - wraz z maleniem długości fali współczynnik załamania również maleje

• Grubość pozorna - Wskutek załamania światła odległości przedmiotów umieszczonych w ośrodku optycznie gęstszym obserwowane z powietrza wydają się mniejsze, np.:

• szyba sprawia wrażenie cieńszej, niż jest w rzeczywistości

• przedmioty w wodzie wydają się bliższe powierzchni

• Współczynnik odbicia przy padaniu prostopadłym na powierzchnię rozgraniczającą ośrodki o różnych współczynnikach załamania

Promień OA prostopadły do powierzchni granicznej wychodzi bez załamania, natomiast OB tworzy z normalną wewnątrz szkła kąt
, a w powietrzu kąt
, większy od
wskutek załamania. Obserwowane promienie wychodzące

z płytki są rozbieżne, ich przedłużenia przecinają się w punkcie O_1­ tworząc obraz pozorny. Odległość O₁A równa h stanowi pozorną grubość płytki, podczas, gdy AO=d jest grubością rzeczywistą.
Ponieważ
a dla małych kątów
, to widać z rysunku, że

.

• 
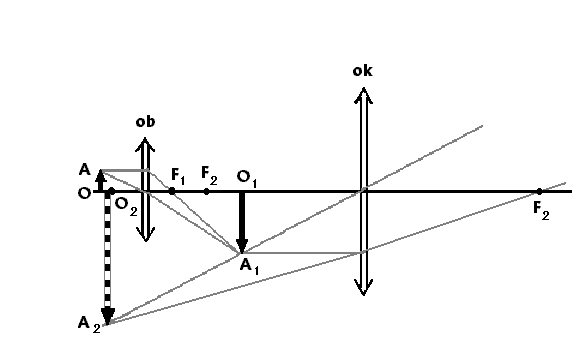
  Bieg promieni w mikroskopie

III. Wyposażenie stanowiska

W doświadczeniu współczynnik załamania wyznacza się z porównania grubości rzeczywistej z grubością pozorną. Do pomiaru grubości rzeczywistej korzysta się ze śruby mikrometrycznej. Do pomiaru grubości pozornej wykorzystuje się mikroskop zaopatrzony w czujnik położenia do określania wielkości przesuwu obiektywu mikroskopu. Elementami dla których określany jest współczynnik załamania są

płasko-równoległe i przezroczyste płytki szkła i pleksiglasu.

IV. Wykonanie pomiaru

1. Zmierzyć śrubą mikrometryczną grubość rzeczywistą płytek. Pomiar wykonać kilkakrotnie.

2. Narysować flamastrem na każdej z powierzchni płytki linię tak, by linie te się krzyżowały. Linie te mają służyć do łatwiejszego ustawienia ostrości górnej i dolnej powierzchni płytki w mikroskopie i do identyfikacji powierzchni.

3. Po umieszczeniu płytki na stoliku mikroskopu ustawić na ostrość obraz linii na jednej z powierzchni płytki. Odczytać wskazanie czujnika.

4. Ustawić na ostrość obraz linii na drugiej powierzchni i dokonać odczytu czujnika.

5. Czynności z punktów 3 i 4 powtórzyć dziesięciokrotnie.

6. Wyniki zapisywać w tabeli:

V. Wyniki pomiaru

Płytka

D

‾D

d1

d2

‾d1

‾d2

‾d1-‾d2

n

VI. Opracowanie wyników

1. Średni błąd kwadratowy wartości średniej odczytu wskazania czujnika dla powierzchni górnej i dolnej

2. Grubość pozorna płytki

, gdzie

Płytka
duża prostokątna	0,03 mm	0,04 mm	0,05 mm
okrągła	0,02 mm	0,02 mm	0,03 mm
kwadratowa	0,02 mm	0,02 mm	0,03 mm
mała prostokątna	0,02 mm	0,02 mm	0,02 mm

3. Błąd wyznaczenia współczynnika załamania

Zastępując przyrosty maksymalnymi błędami oraz zamieniając różnicę błędów na sumę ostatecznie otrzymujemy wzór na błąd współczynnika załamania

gdzie ΔD = 0,01mm

Płytka	N	ΔN
duża prostokątna	1,492	0,028
okrągła	1,527	0,018
kwadratowa	1,462	0,025
mała prostokątna	1,518	0,032

4. Możliwość wyznaczania zależności współczynnika załamania od długości fali

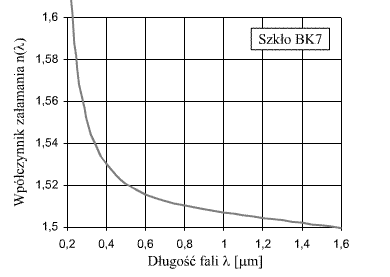
Istnieje możliwość wyznaczenia zależności
, czyli tak zwanej dyspersji.

W celu wyznaczenia zależności n(λ) należy do mierzenia grubości pozornej płytki użyć światła monochromatycznego. Dla każdej długości światła należy wyznaczyć współczynnik załamania, następnie na odpowiednim wykresie przedstawić funkcję dyspersję.

---