1. Zagadnienia do opracowania:

1.1. Widmo promieniowania elektromagnetycznego.

Znamy szerokie widmo fal elektromagnetycznych, zilustrowane na rysunku 1. Dominującym źródłem promieniowania, w którym wykształciliśmy się i do którego przystosowaliśmy się jako gatunek, jest Słońce. Ale tkwimy też w gąszczu sygnałów radiowych i telewizyjnych. Mogą dosięgać nas mikrofale z radarów i telefonicznych stacji przekaźnikowych. Wokół są także fale wytwarzane w żarówkach, w nagrzanych silnikach samochodowych, w aparatach rentgenowskich, w lampach błyskowych, a także w zakopanych materiałach promieniotwórczych. Ponadto dociera do nas promieniowanie z gwiazd i innych obiektów naszej Galaktyki i z innych galaktyk. Fale elektromagnetyczne wędrują również w drugą stronę. Sygnały telewizyjne, wysyłane z Ziemi niosą teraz wiadomości o nas do wszystkich mieszkańców kosmosu (jeśli tacy istnieją i mogą je odebrać).

Podziałki skali długości fali na rysunku 1 są kolejnymi potęgami liczby 10. Skala nie ma końców, nie ma bowiem żadnego naturalnego ograniczenia długości fali elektromagnetycznej z żadnej ze stron. Na rysunku 1 niektóre zakresy widma fal elektromagnetycznych opatrzone są znajomymi etykietkami, jak np. promieniowanie rentgenowskie i fale radiowe. Te etykietki odnotowują z grubsza zdefiniowane zakresy długości fali. w których powszechnie używa się pewnych, określonych źródeł i detektorów fal elektromagnetycznych. Inne zakresy na rysunku 1, jak np. te oznaczone jako zakresy radiowe bądź telewizyjne, reprezentują określone długości pasm przypisanych prawnie do celów komercyjnych bądź innych zastosowań. W widmie elektromagnetycznym nie ma przerw i wszystkie fale elektromagnetyczne, niezależnie od tego, do jakiego zakresu widma należą, rozchodzą się w próżni z taką samą prędkością c.

Dla nas szczególnie interesującym zakresem widma jest oczywiście zakres widzialny. Środek obszaru widzialnego znajduje się przy ok. 555 nm, czemu odpowiada barwa żółtozielona. Granice obszaru widzialnego nie są dobrze zdefiniowane, gdyż krzywa czułości oka dąży do zera zarówno po stronie fal dłuższych, jak i po stronie krótszych. Jeżeli na przykład przyjmiemy, że granicę taką stanowi poziom, przy którym czułość oka spada do 1% jej wartości maksymalnej, to granice te wynoszą wtedy 430 nm i 690 nm; oko może również wykrywać fale elektromagnetyczne o długościach fali nieco wykraczających poza te granice, jeżeli ich natężenia są dostatecznie duże.

Rys 1. Widmo promieniowania

elektromagnetycznego.

1.2. Zachowanie się światła na granicy dwóch ośrodków.

Na granicy dwóch ośrodków izotropowych 1 i 2, w których światło rozchodzi się z prędkościami v₁ i v₂ promień świetlny, wchodząc z ośrodka 1 do ośrodka 2, zmienia kierunek swego biegu - jego część ulegnie odbiciu a pozostała część wejdzie do drugiego ośrodka tworząc tzw. promień załamany.

Możliwe są trzy sytuacje:

• 
  Jeżeli n₂ jest równe n₁ to θ₁ jest równe θ₂. W takim przypadku załamanie nie następuje, promień nie zostaje odchylony od swojego pierwotnego kierunku, tak jak to pokazano na rysunku 2a

Rys 2a. Załamanie światła na granicy

dwóch ośrodków.

• Jeżeli n₂ jest większe od n₁, to θ₂, jest mniejsze od θ₁. W takim przypadku po załamaniu promień jest odchylany od swojego pierwotnego kierunku (od kierunku promienia padającego) w stronę do normalnej, tak jak pokazano na rysunku 2b.

Rys 2b. Załamanie światła na granicy

dwóch ośrodków.

• Jeżeli n₂ jest mniejsze od n₁, to θ₂ jest większe od θ₁. W takim przypadku po załamaniu promień jest odchylany od swojego pierwotnego kierunku (od kierunku promienia padającego) w stronę od normalnej, tak jak pokazano na rysunku 2c.

Rys 2c. Załamanie światła na granicy

dwóch ośrodków.

Załamanie nigdy nie może odchylić promienia załamanego od jego pierwotnego kierunku tak dalece, aby mógł się on znaleźć po tej samej stronie normalnej co promień padający.

W każdym przypadku promień padający, promień załamany i prostopadła do powierzchni granicznej leżą w jednej płaszczyźnie i spełniają poniższą zależność:

Zależność ta wyraża prawo załamania podane przez Snelliusa.

Stałą wartość stosunku sinusów kątów padania i załamania równą stosunkowi prędkości rozchodzenia się światła w ośrodkach 1 i 2 nazywamy współczynnikiem załamania ośrodka 2 względem ośrodka 1 i oznaczamy przez n_2,1. Stosunek prędkości c rozchodzenia się światła w próżni do prędkości rozchodzenia się światła w danym ośrodku nazywamy bezwzględnym współczynnikiem załamania światła tego ośrodka:

Prawo Snelliusa przyjmuje wówczas postać:

lub

1.3. Zasada działania mikroskopu optycznego.

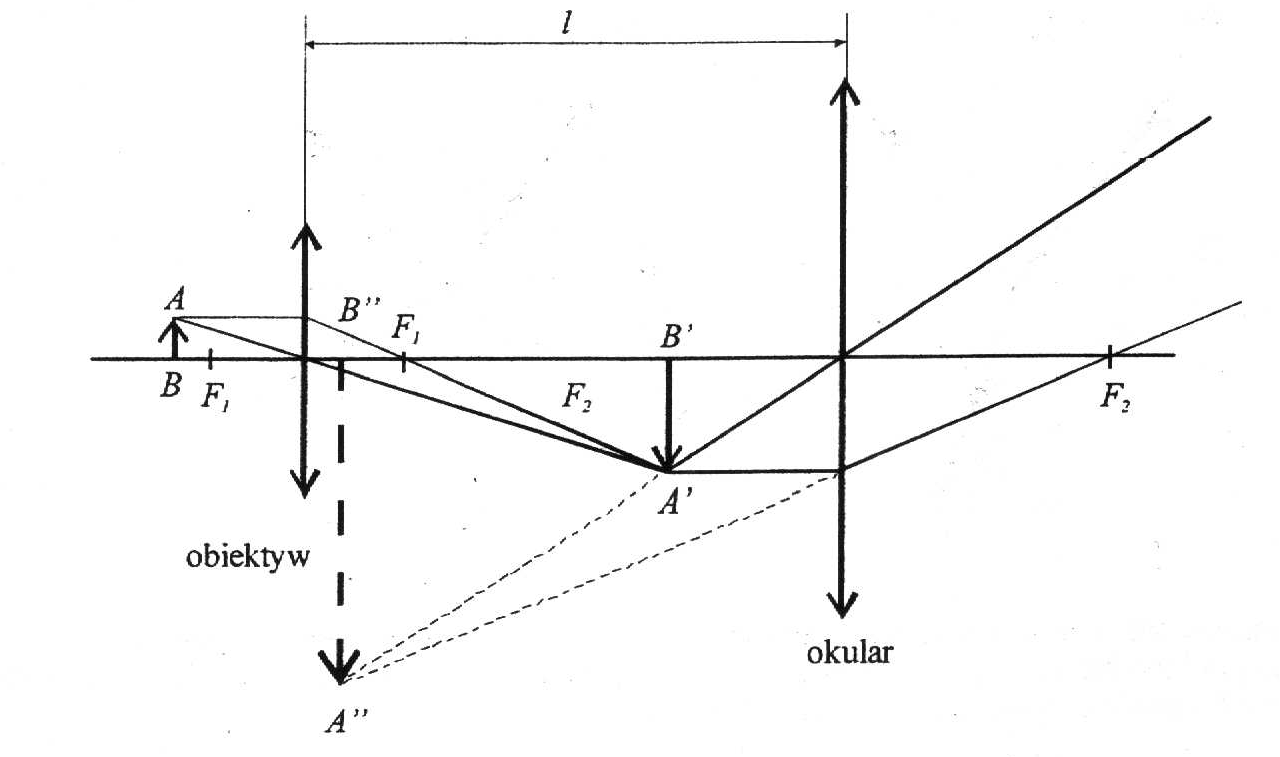
Mikroskop składa się z dwóch soczewek skupiających: obiektywu i okularu ustawionych w odległości większej niż suma ogniskowych zastosowanych soczewek. Najczęściej obiektyw składa z układu soczewek, przez co minimalizowane są wady odwzorowań (np. aberracja sferyczna i chromatyczna) a okular z pojedynczej soczewki. Obiektyw daje obraz rzeczywisty, odwrócony i powiększony. Oglądany przedmiot umieszcza się przed obiektywem w odległości nieco większej niż jego ogniskowa f₁. Druga soczewka (okular) działa jak lupa i daje obraz urojony, powiększony i prosty. Na rysunku 3 przedstawiono powstawanie obrazu w mikroskopie optycznym.

Rys 2c. Załamanie światła na granicy

dwóch ośrodków.

2. Metodologia wykonania pomiarów

2.1. Objaśnienie metody.

Metoda wyznaczania współczynnika załamania przy pomocy mikroskopu polega na obserwacji zarysowań górnej i dolnej powierzchni płasko-równoległej płytki.

Promienie a i b są wybranymi promieniami spośród tworzących obraz punktu O na siatkówce oka (rysunek 4). Załamany w punkcie O promień a ulega ponownemu załamaniu w punkcie A. Jeżeli na powierzchni I płytki narysujemy jedną linię, a na powierzchni II narysujemy krzyżującą się z nią drugą linię, to obserwując je przez mikroskop, widzi się obraz linii narysowanej na powierzchni II w punkcie O, lecz w miejscu oznaczonym na rysunku O', ponieważ nasze oko widzi obiekt po liniach prostych. Promień b prostopadły do płytki nie ulega załamaniu. Oznaczamy grubość płytki przez d = OO", zaś grubość pozorną d' = O'O", trygonometrycznych zależności wynika:

stąd:

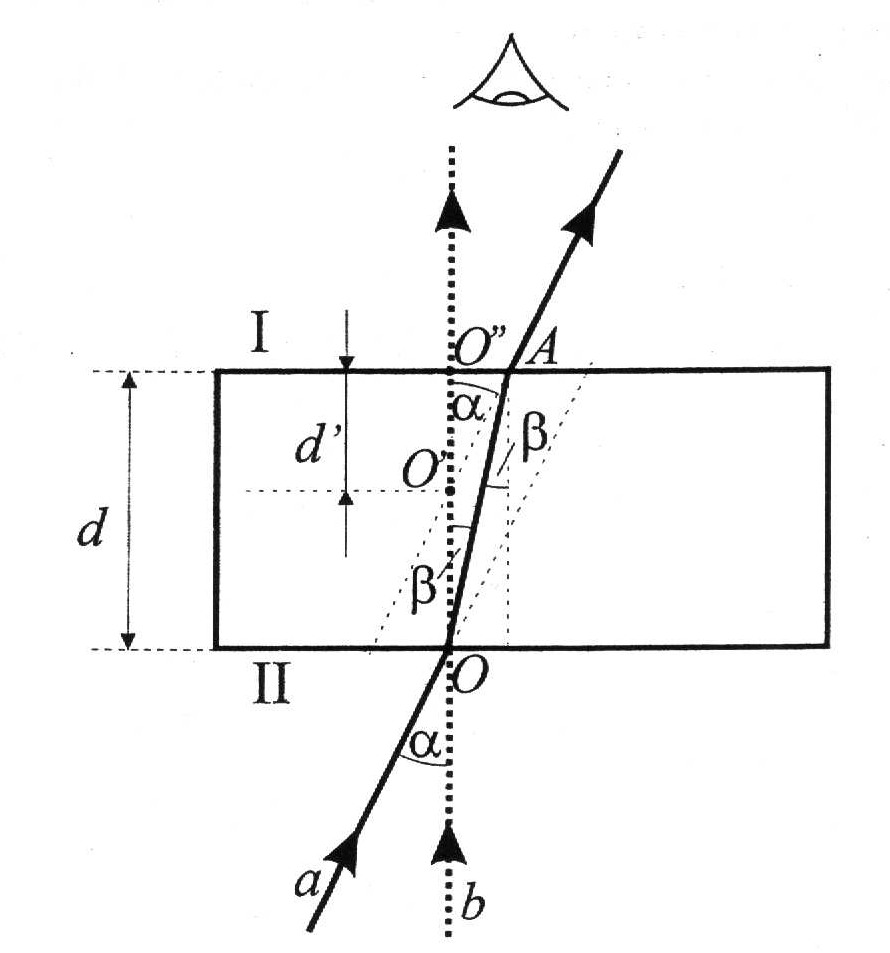
Dla niewielkich kątów spełniony jest warunek tgα ≈ sinα ponieważ kąty padania i załamania są małe, ostatnia nierówności możemy zapisać jako:

Ostatecznie otrzymujemy:

gdzie, n_w jest względnym współczynnikiem załamania szkła względem powietrza.

2.2. Kolejność wykonywanych czynności.

1. Wybrać dwie płytki płasko-równoległe z różnych materiałów i starannie je oczyścić.

2. Śrubą mikrometryczną zmierzyć grubość płytek d. Pomiary powtórzyć 10 razy dla każdej płytki: (mierząc w różnych miejscach w okolicy skrzyżowania narysowanych linii).

3. Przygotować mikroskop do pomiaru - ustawić zwierciadło tak, aby pole widzenia było oświetlone.

4. Umieścić płytkę na stoliku mikroskopu. Pokręcając śrubą przesuwu pionowego stolika ustawić go tak, aby widoczna była ostro kreska narysowana na górnej powierzchni płytki.

5. Kręcąc śrubą znajdującą się na stopce czujnika dołączonego do mikroskopu ustawić wskazanie czujnika d₁ w okolicy lmm. Wartość tę zapisać w tabeli.

6. Podnieść stolik tak, aby otrzymać ostry obraz kreski znajdującej się na dolnej powierzchni płytki. Zapisać wskazanie czujnika d₂.

7. Pomiary powtórzyć dziesięciokrotnie. Obliczyć pozorną grubość płytki d' = d₂ - d₁.

8. Powtórzyć pomiary 4 -0- 7 dla drugiej płytki.

3. Tabele pomiarowe

Tabela 1

Materiał	d		d1	d2	d'		n ± u(n)
		[mm]	[mm]	[mm]	[mm]	[mm]	[mm]	[ - ]
	Plexi	3,56	3,572±0,0013	1,00	4,20	2,36	2,344±0,059	1,565±0,029
		3,57			1,12	4,59			2,31
		3,61			0,82	4,27			2,32
		3,54			1,19	4,11			2,40
		3,55			1,20	4,40			2,33
		3,58			1,02	4,12			2,32
		3,60			1,18	4,46			2,30
		3,58			1,27	4,39			2,38
		3,56			1,15	4,07			2,35
		3,57			1,31	4,39			2,37

Tabela 2

Materiał	d		d1	d2	d'		n ± u(n)
		[mm]	[mm]	[mm]	[mm]	[mm]	[mm]	[ - ]
	Szkło	5,85	5,8400±0,0026	1,00	5,24	4,24	3,958±0,094	1,475±0,035
		5,81			1,20	5,70			4,50
		5,79			1,46	4,98			3,52
		5,81			1,55	5,28			3,73
		5,82			1,19	5,01			3,82
		5,79			0,91	5,11			4,20
		5,84			1,19	5,19			4,00
		5,82			1,19	4,85			3,66
		5,80			1,22	5,12			3,90
		5,80			0,89	4,90			4,01

4. Obliczenia

4.1. Obliczanie grubości pozornej płytek d':

Wzór:

Przykłady obliczenia:

dla plexi

dla szkła

4.2. Obliczanie średniej grubości pozornej
płytek:

Wzór:

Obliczenia:

dla plexi

dla szkła

4.3. Obliczanie niepewności pomiaru grubości pozornej płytek (metoda typu A):

Wzór:

Obliczenia:

dla plexi

dla szkła

4.4. Obliczanie średniej grubości płytek:

Wzór:

Obliczenia:

dla plexi

dla szkła

4.5. Obliczanie niepewności pomiaru grubości płytki (metoda typu A):

Wzór:

Obliczenia:

dla plexi

dla szkła

4.6. Obliczanie względnego współczynnika załamania światła:

Wzór:

Obliczenia:

dla plexi

dla szkła

4.7. Obliczanie niepewności względnego współczynnika załamania światła (korzystając z prawa przenoszenia niepewności):

Wzór:

Obliczenia:

dla plexi

dla szkła

5. Wnioski i spostrzeżenia

1. Podczas wykonywania ćwiczenia określaliśmy względne współczynniki załamania światła, plexi względem powietrza i szkła względem powietrza, przeprowadzone pomiary wykazały, że plexi ma nieco większy względny współczynnik załamania a niżeli szkoło.

2. Jednakże niepewność pomiaru względnego współczynnika załamania szkła względem powietrza jest większa niż niepewność pomiaru współczynnika załamania plexi, co wynika z większych niepewności pomiaru grubości oraz grubości pozornej płytki wykonanej ze szkła.

3. Większa niepewność pomiaru grubości płytki wykonanej ze szkła wynika z procesu technologicznego szkła, który stwarza więcej możliwości powstania niedokładności a niżeli proces technologiczny plexi.

---