Optyka

Kolejne zastosowanie równań Maxwella to przypadek gdy długość fal jest pomijalnie mała z rozmiarami urządzeń i struktur z którymi oddziaływuje. Znane równania optyki geometrycznej wynikają w oczywisty sposób z tych równań na granicy ośrodków.

Dokonamy krótkiego przeglądu poczynając od optyki geometrycznej poprzez Gaussowską i kończąc na optyce nieliniowej.

Odbicie i załamanie

Poprzednio pokazaliśmy, że fala płaska TEM rozchodząca się w jednorodnym ośrodku ma następujące właściwości:

• 
  , gdzie kierunek pola elektrycznego
  jest prostopadły do kierunku rozchodzenia się fali
  .

• Pole magnetyczne jest proporcjonalne i prostopadłe do pola elektrycznego i wynosi:
  .

• Prędkość fali wynosi
  a liczba falowa
  

Materiały optyczne są zwyczajowo opisywane przez współczynnik załamania n, który jest ilorazem prędkości światła w próżni do prędkości światła w danym materiale:

typowa wartość dla szkła wynosi około n=1,5.

Zauważmy, że iloraz

jest niezależny od materiału i określony jest jedynie przez częstość fali. To oznacza, że gdy fala na swej drodze przechodzi przez ośrodki o różnych współczynnikach załamania to nie zmienia swojej częstości tyko zmienia się prędkość fali i jej długość.

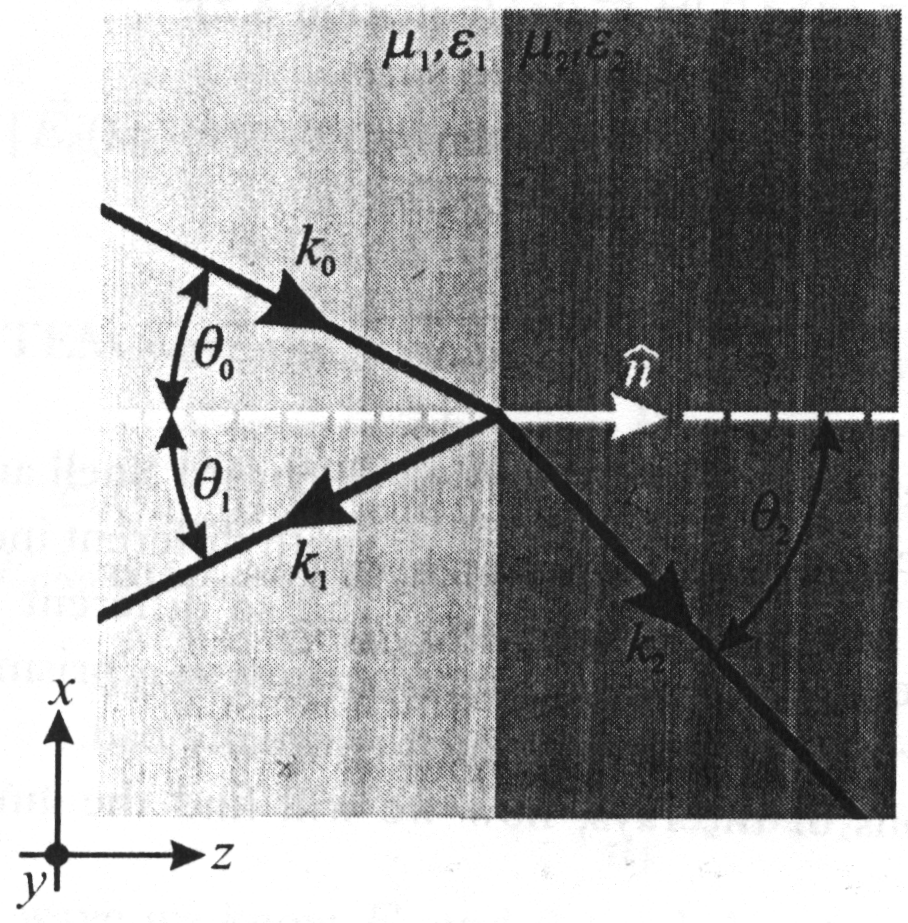
Pokazaliśmy już, że na granicy dwóch ośrodków a i b, gdy nie występują powierzchniowe ładunki oraz prądy zarówno normalne składowe D i B są ciągłe

Jak i ciągłe są składowe styczne do powierzchni wektorów E i H:

gdzie
jest wersorem normalnym do powierzchni.

Rozważmy teraz płaską falę elektromagnetyczną podającą na granicę dwóch dielektryków pod dowolnym kątem i pozwólmy jej zarówno na odbicie jak i przejście przez tą granicę. Z warunku ciągłości składowej stycznej pola E otrzymujemy:

Częstości fali w różnych ośrodkach muszą być równe
zatem:

Ponieważ jednak k₀ i k₁ są sobie równe (fala rozchodzi się w tym samym ośrodku wobec czego jej długość jest taka sama) otrzymujemy:

kąt padania równa się katowi odbicia

Druga zależność wynika z relacji
a zatem

Powyższe równanie odkryte około roku 1621 przez Willebrorda Snella nosi nazwę od jego nazwiska.

Należy zauważyć ponadto, że fale o różnych częstościach (różnych barwach) będą załamywały się pod różnymi kątami. To zjawisko nosi nazwę dyspersji chromatycznej i jest zwykle korzystne w pryzmatach (spektrometry) gdy jednocześnie w soczewkach zwykle jest kłopotliwe po powoduje tak zwaną aberację chromatyczną.

Znaleźliśmy już kierunki fal teraz przyszła pora na amplitudy. Wróćmy do równań ciągłości na granicy ośrodków.

Ponieważ wektory E i H w fali elektromagnetycznej są proporcjonalne otrzymujemy

ponieważ większość materiałów dielektrycznych względną przenikalność magnetyczną ma bliską jedności.

Podstawiają ostatni wynik do poprzedniego równania

Wynik należy rozpatrzyć w dwóch częściach: oddzielnie składową normalną do płaszczyzny padania i oddzielnie składową w płaszczyźnie padania fali (E_y=0).

• E prostopadłe do płaszczyzny padania. Równanie ciągłości prowadzi do równania skalarnego (?)

Powróćmy do równania:
i wykorzystajmy znaną zależność

Ponieważ E jest prostopadłe do k (Fala TEM)

Ponieważ znamy amplitudę i kat fali padającej a z prawa odbicia i prawa Snella kąt odbicia i kąt załamania możemy obliczyć amplitudę fali odbitej i załamanej:

• E w płaszczyźnie padania

Znowu trochę trygonometrycznej algebry i otrzymujemy

Zaznaczone równania noszą nazwę równań Fresnela

Z równań Fresnela wynika kilka ciekawych wniosków:

• 
  wniosek trywialny, w tym samym materiale nie ma odbicia.

• 
  Promień padający i załamany są prostopadłe składowa pola odbitego w płaszczyźnie padania znika. Promień odbity jest całkowicie liniowo spolaryzowany. Kąt padania nazywamy wówczas kątem Brewstera i możemy w prosty sposób otrzymać jego wartość z prawa Snella:
  

• Kolejnym ważnym kątem jest kąt krytyczny dla odbicia dla którego kąt promienia załamanego wynosi π/2
  

Gdy n₂ jest mniejszy od n₁ istnieje kąt podania powyżej którego mamy do czynienia ze zjawiskiem całkowitego wewnętrznego odbicia wykorzystywanym między innymi w światłowodach.

Optyka Geometryczna.

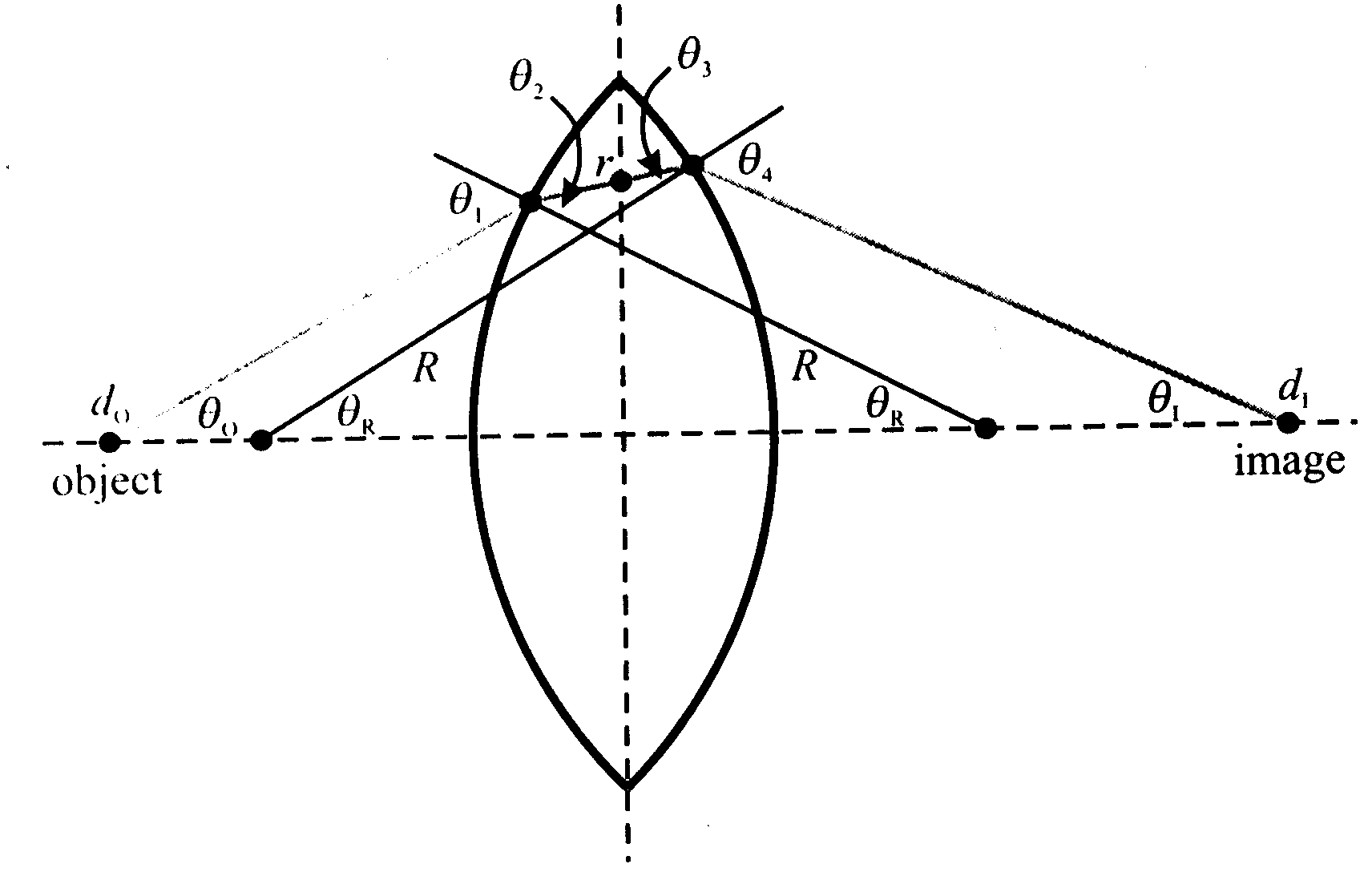
W rozważaniach z zakresu optyki geometrycznej zakładamy, że długość rozważanej fali świetlnej jest mała w porównaniu do odległości, które musi ona pokonać w układzie, oraz że mamy do czynienia z odbiciem i załamaniem fali płaskiej na sferycznych soczewkach o promieniach krzywizn R i współczynniku załamania n. Dodatkowo dla uproszczenia rozważań rozpatruje się jedynie promienie przyosiowe o niewielkich kątach θ odchylenia od osi optycznej, dla których sinθ≈θ i zakłada niewielką grubość soczewek. Teraz wystarczy tylko trochę trygonometrii aby otrzymać równanie soczewkowe.

Z sumy kątów w trójkącie mamy:

I podobnie dla promieni wychodzących z soczewki:

Co po dodaniu tych dwóch równań daje

korzystając następnie z prawa Snella

I wreszcie kompilując ostatnie równania otrzymujemy uproszczone równanie soczewki cienkiej:

gdzie f jest długością ogniskowej.

Parametry soczewek

(F number- jasność) stosunek długości ogniskowej do średnicy

Apertura numeryczna - połowa kąta zakreślonego od ogniska do brzegów soczewki pomnożona przez współczynnik załamania.

Rachunek macierzowy układów optycznych.

Poprzednie obliczenia nie były zbyt skomplikowane jednak sytuacja ulega radykalnej zmianie, gdy musimy obliczyć układ wielosoczewkowy.

Przekształcenie optyczne wykonywane przez układ można zapisać w formie operacji na macierzach:

gdzie macierz kwadratowa przedstawia operację optyczną na wiązce o promieniu r liczonym od osi optycznej do elementu transformującego a r'=dr/dz opisuje nachylenie wiązki.

Przykład 1. Jednorodny ośrodek o grubości w - macierz przekształcenia:

Przykład 2.

Znajdźmy teraz macierz soczewki cienkiej:

co można zapisać jako
stad macierz przekształcenia ma prostą postać:

Przykład 3. Prawo Snella ma prostą macierz

Przykład 4. Wałek o długości d w którym współczynnik załamania zmienia się z kwadratem odległości od osi optycznej.

gdzie
Jest to specjalna soczewka o zmiennym współczynniku załamania służąca do wprowadzania wiązki do światłowodu. GRIN (Graded Index of refraction).

Transformacje optyczne

Czytając poniższe rozważania, należy pamiętać, że fale mają także przesunięcie fazowe zależne od drogi optycznej którą pokonują. Może to prowadzić do niespodziewanych efektów interferencyjnych.

Rozważmy falę płaską padającą na cienką soczewkę jak na rysunku.

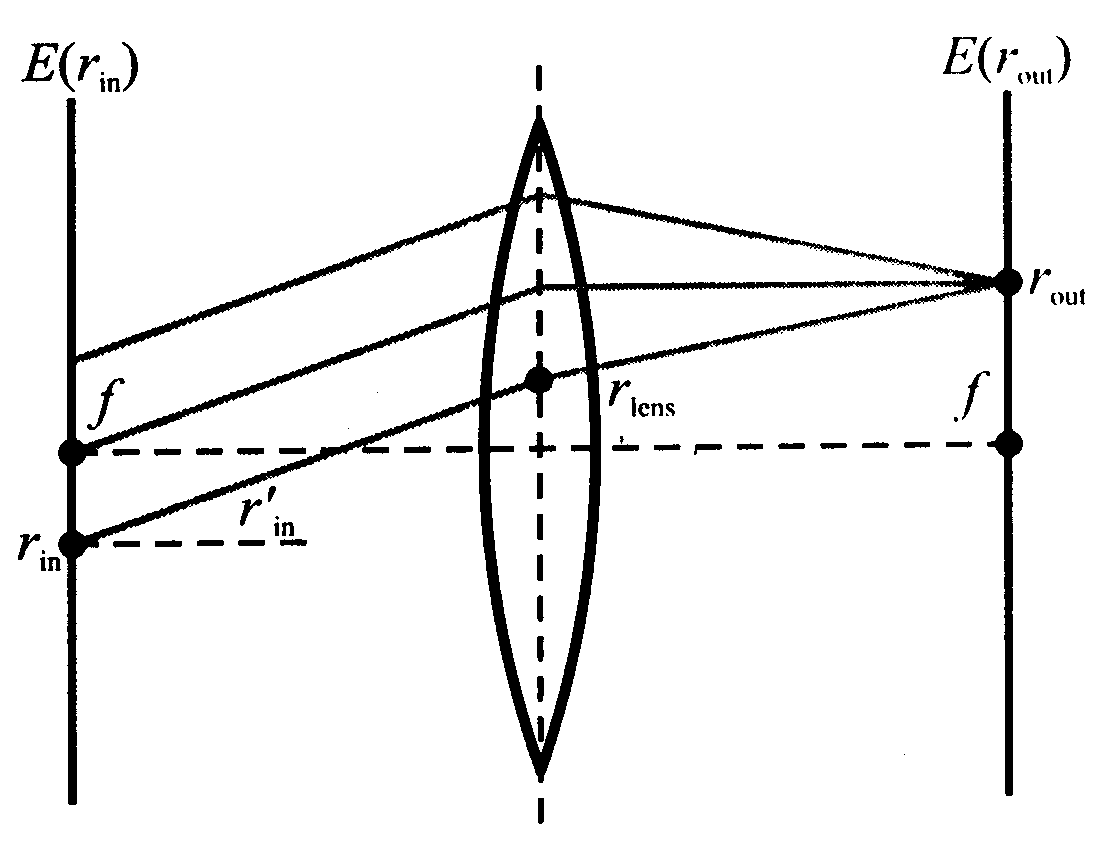
Fala pokonuje pusta przestrzeń na odległości f
, następnie pada na soczewkę o ogniskowej f
i ponownie pokonuje pusta przestrzeń na odległości f

Otrzymana w wyniku transformacja wygląda następująco:

Jak widać z rysunku fale wychodzące z różnych punktów r_in dochodzą do tego samego punktu r_ouot mają do pokonania różne drogi, są więc poprzesuwane w fazie. Efekt interferencji tych fal teraz obliczymy.

Droga promienia od punktu startowego do soczewki wyniesie więc po uwzględnieniu przybliżenia promieni przyosiowych

i podobnie odległość od soczewki do płaszczyzny ogniskowej

Na przesunięcie fazowe będzie miała także wpływ droga pokonana przez promień w soczewce o grubości 2d₀ na osi optycznej i krzywiźnie R. Obliczony dystans wyniesie:

Zakładając współczynnik załamania wynoszący 1 w przestrzeni poza soczewką otrzymujemy związek pomiędzy liczbami falowymi w soczewce i poza nią

Dodatkowe przesunięcie w fazie na skutek przejścia przez soczewkę wyniesie

Pamiętając jednak, że na podstawie wzoru soczewkowego R=2f(n-1)

Ostatni krok to wysumowanie po wszystkich falach wchodzących do układu z uwzgl ędnieniem obliczonego przesunięcia fazowego

Wynik w pierwszym momencie może wydawać się niezrozumiałym, a jest przecież bardzo podobny do transformaty Fouriera.

Wprowadzając koherentne oświetlenie na płaszczyznę ogniskową cienka soczewka daje na wyjściu transformatę Fouriera pomnożoną przez dodatkową współczynnik fazowy.

Ponieważ obliczenia te są przeprowadzane z prędkością światła i ponadto pracują na dwuwymiarowym sygnale wejściowym mogą być wykorzystywane w algorytmach bazujących na transformatach Fouriera. (np. filtrowanie...). Oczywiście takie układy ze względu na efekty nieliniowe nie są doskonałe ale mogą być bardzo użyteczne.

Granice optyki geometrycznej

Według wyników optyki geometrycznej fala świetlna może być zogniskowana do punktu dowolnie małych rozmiarów i osiągać w nim nieskończenie duże gęstości energii. To jest oczywiście niemożliwe ponieważ przybliżenie światła falą płaska nie jest słuszne, gdy rozpatrywane rozmiary są porównywalnie z jej długością. Powróćmy więc do równania falowego.

Rozważmy źródło punktowe emitujące falę sferyczną
. Gdybyśmy chcieli odwrócić sytuację i zogniskować światło w punkcie musiałoby ono docierać ze wszystkich stron, a to ze względu na skończone rozmiary soczewek nie jest możliwe. Fala nie może jednocześnie spełniać warunków brzegowych na soczewce i być falą idealnie sferyczną.

Aby określić rozmiary ogniskowanej plamki musimy ją powiązać z kątem aperturowym. Z oczywistych względów rozważania przeprowadzimy w dwóch wymiarach. Łatwo jest je oczywiście uogólnić na trzy wymiary. Załóżmy falę sferyczną nadchodzącą w koncie aperturowym θ

Przeprowadźmy proste całkowanie

Ostatnie przybliżenie otrzymano z warunku

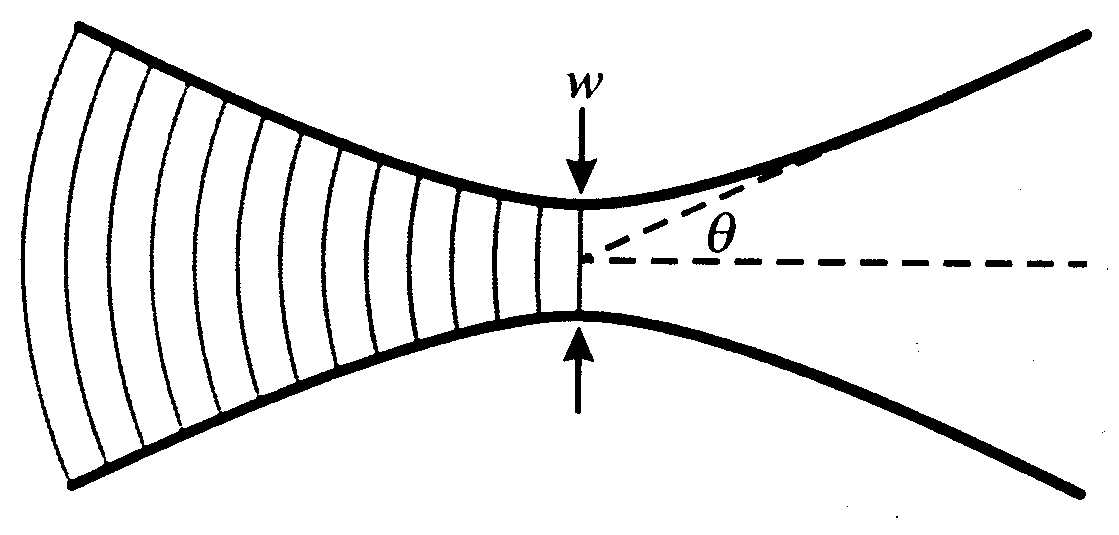
Jeżeli teraz zapytamy się o granice gdzie argument funkcji cos równa się 1

Jak widać kąt dyspersji fali jest proporcjonalny do jej długości i odwrotnie proporcjonalny do rozmiarów źródła i współczynnika załamania. Jest to podstawowy problem związany ze zdolnością rozdzielczą urządzeń optycznych (mikroskopów-ciecze imersyjne. teleskopy, niebieskie lasery do zapisu optycznego danych).

Aby rozwiązać problem dyfrakcji fali w ogólności, trzeba rozwiązać równania Maxwella w układzie cylindrycznym a nie jest to trywialne.

Ograniczenia, które tu zaprezentowaliśmy noszą nazwę optyki Gaussowskiej, ze względu na standardowe odchylenie w wiązki światła od osi optycznej.

Gęstość energii jaką jednak udaje się uzyskiwać jest jednak i tak duża, może przewyższać energię pól wewnątrz atomowych i powodować nieliniowe zjawiska optyczne.

Pierwszy stopień korekty zjawiska polaryzacji elektrycznej

Nieliniowy współczynnik optyczny d₂ jest w ogólności zależny od orientacji w próbce w stosunku do tzw. osi optycznych.

Prostszy zapis skalarny

Współczynnik nieliniowy jest w typowych materiałach mały rzędu 10^-12m/V dlatego jest najczęściej traktowany jako mała poprawka do polaryzacji.

jeżeli podstawimy
to prawa strona przyjmie postać
i pełni rolę siły wymuszającej drgania o dwukrotnie większej częstości. Zjawisko to nazywa się generacją drugiej harmonicznej i wykorzystuje się do wytwarzania promienia laserowego o małej długości.

Laser Nd YAG (Nd³⁺:Y₃Al₅O₁₂) 1064nm przy pomocy KDP (KH₂PO₄) otrzymujemy 532nm.

Inne wykorzystanie zjawiska nieliniowości oparte jest na oświetlaniu kryształu dwoma laserami.

Powoduje to generowanie częstości różnicowych i sumacyjnych i jest wykorzystywane w parametrycznym wzmacniaczu optycznym OPA.

---