Mateusz Mościński

Gr. 4A s.1

Temat: Wyznaczanie refrakcji molekularnej cieczy.

Cel :

• Wyznaczenie współczynnika załamania światła dla roztworu etanolu

• Sporządzenie wykresu zależności współczynnika załamania światła roztworów etanolu od stężenia tych roztworów oraz wyznaczenie współczynnika załamania światła dla czystego etanolu (100%).

• Wyznaczanie nieznanego stężenia roztworu etanolu.

• Badanie egzaltacji refrakcji i struktury etanolu.

• Badanie refrakcji roztworu etanolu o wybranym stężeniu (40%)

• Badanie struktury gliceryny.

• Wyznaczenie momentu dipolowego cząsteczek wody destylowanej, etanolu i gliceryny.

Tabela pomiarów:

Badana substancja		Współczynnik załamania światła n
Roztwory etanolu o różnych stężeniach c[%]	5%	1,335
		10%	1,338
		15%	1,342
		20%	1,345
		25%	1,347
		30%	1,352
		40%	1,355
		50%	1,358
		60%	1,361
		70%	1,362
		80%	1,362
		90%	1,361
		95%	1,361
		x%	1,356
Gliceryna		1,471
Woda		1,332

Wyznaczanie nieznanego stężenia etanolu:

Współczynnik załamania światła (n) jest wielkością zależną od stężenia roztworu (c). Znając więc wartość współczynnika można, korzystając z wykresu funkcji n=f(c) wyznaczyć nieznane stężenie badanego roztworu.

Odczytujemy z wykresu wartość stężenia, dla współczynnika załamania n = 1,356

x = 43%

Badanie egzaltacji refrakcji i struktury etanolu:

• Obliczanie refrakcji molowej rozpoczynamy od wyznaczenia współczynnika załamania światła dla 100% roztworu etanolu. W tym celu wykonujemy ekstrapolację wykresu funkcji n=f(c) i odczytujemy wartość współczynnika na osi rzędnych:

n_100% = 1,3605

• Refrakcję molową etanolu liczymy ze wzoru:

,

gdzie: R- refrakcja molowa ;

n - współczynnik załamania światła;

M - masa cząsteczkowa [kg/mol];

ρ - gęstość cieczy [kg/m³].

• Przyjmując dla czystego etanolu gęstość ρ = 789,5 [kg/m³] oraz masę cząsteczkową 1 mola M = 0,046 [kg/mol] obliczamy doświadczalną refrakcję molową:

R_dośw. = 1,2875 · 10^-5 [m³/mol]

• 
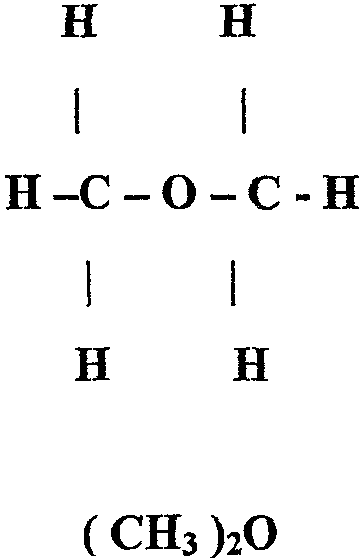
  Korzystając z tabeli refrakcji wiązań oraz zasady addytywności obliczamy refrakcje teoretyczne R_obl. dla przedstawionych struktur etanolu:

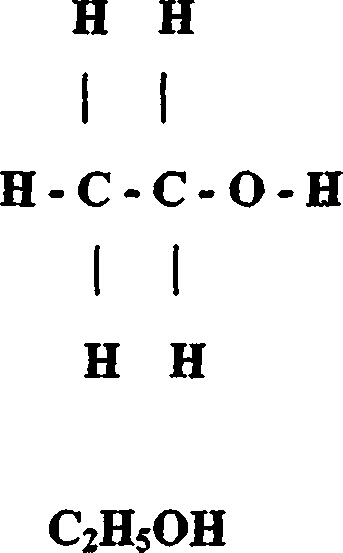
Struktura Pierwsza (R₁) Struktura Druga (R₂)

Tabela refrakcji wiązań:

Wiązanie	Refrakcja [10^-6 m^3/mol]
C ― H	1,68
C ― C	1,30
C ― O	1,54
O ― H	1,66

• W tym celu korzystamy z następującego wzoru na refrakcję molową:

,

gdzie: R_x-x - refrakcje kolejnych wiązań;

i - liczba wiązań w cząsteczce.

• Podstawiając dane do wzoru obliczamy refrakcje teoretyczne:

R₁ = 5·1,68·10^-6 + 1·1,3·10^-6 + 1·1,54·10^-6 + 1·1,66·10^-6 = 1,29·10^-5 [m³/mol]

R_.2 = 6·1,68·10^-6 + 0·1,3·10^-6 + 2·1,54·10^-6 + 0·1,66·10^-6 = 1,316·10^-5 [m³/mol]

• Z porównania wartości refrakcji molowej doświadczalnej i teoretycznej otrzymujemy:

|R_doś. - R₁| = |1,2875·10^-5 - 1,29·10^-5| = 2,5·10^-8 [m³/mol]

|R_doś. - R₂| = |1,2875·10^-5 - 1,316·10^-5| = 2,85·10^-7 [m³/mol]

Dla pierwszej struktury otrzymaliśmy prawie dziesięciokrotnie mniejszą różnicę wartości.

Badanie refrakcji roztworu etanolu o stężeniu c =40%:

1. Obliczając refrakcję teoretyczną R_obl. 40% roztworu etanolu korzystamy ze wzoru:

,

gdzie: R_a i R_w - refrakcje molowe alkoholu i wody;

X_a i X_w - ułamki molowe alkoholu i wody.

Aby uzyskać wartości ułamków molowych korzystamy ze wzorów:

gdzie: p - udział etanolu w roztworze wyrażony w ułamku;

M_A i M_W - masy molowe alkoholu i wody.

Dla 40% roztworu etanolu przyjmujemy następujące wartości:

p = 0,4;

M_A = 46 [g/mol];

M_W = 18 [g/mol].

Podstawiając je do wzoru i obliczając poszczególne wartości otrzymujemy wyniki:

X_A = 0,206897

X_w =1- 0,206897= 0,79310345

• Refrakcja teoretyczna wody i etanolu wynosi:

R_W= 2∙R_O-H = 2∙1,66∙10^-6 = 0,332∙10^-5 [m³/mol]

R_A = 1,29∙10^-5 [m³/mol].

• Po wyliczeniu wszystkich wartości możemy obliczyć teoretyczną refrakcję roztworu etanolu o stężeniu c = 40%, podstawiając je do wzoru:

.

R_obl. = 0,206897∙1,29∙10^-5 + 0,79310345 ∙ 0,332∙10^-5 = 0,53∙10^-5 [m³/mol]

2. Obliczając refrakcję doświadczalną R_dośw.. 40% roztworu etanolu korzystamy ze wzoru:

,

gdzie M zastępujemy wyrażeniem:

• Dla roztworu o stężeniu c = 40% przyjmujemy wartości:

ρ = 936,8 [kg/m³];

n_40%. = 1,355;

stąd:

M = 0,206897∙0,046 + 0,79310345∙0,018 = 0,023793 [kg/mol].

• Po podstawieniu i wyliczeniu otrzymujemy:

R_dośw = 0,553531 10^-5 [m³/mol]

3. Egzaltacja refrakcji roztworu etanolu o stężeniu c = 40%:

|R_obl. - R_dośw.| = | 0,53∙10^-5 - 0,553531 ∙10^-5 | = 0,233∙10^-8 [m³/mol].

Badanie struktury gliceryny:

• Obliczamy doświadczalną refrakcję molową gliceryny ze wzoru:

,

przyjmując w 20°C :

ρ = 1233 [kg/m³];

M = 0,092 [kg/mol];

n = 1,471

Stąd:

R_dośw. = 2,08557 ∙10^-5

• Obliczamy teoretyczną refrakcję molową korzystając z tabeli refrakcji wiązań oraz zasady addytywności dla dwóch proponowanych struktur gliceryny:

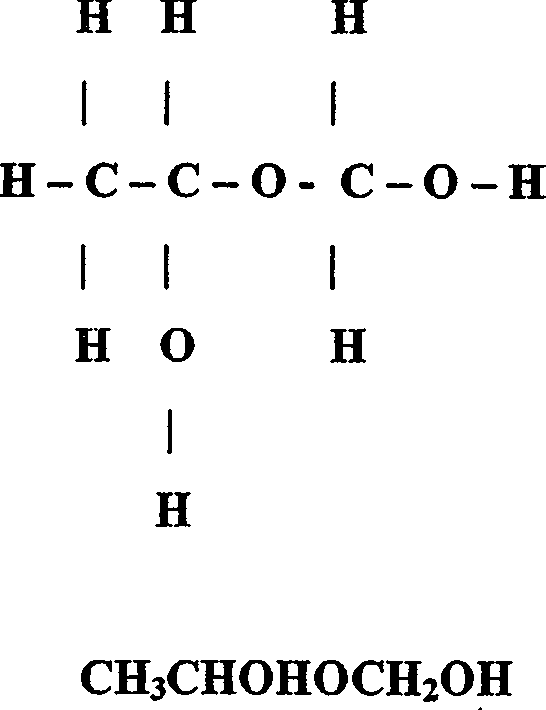
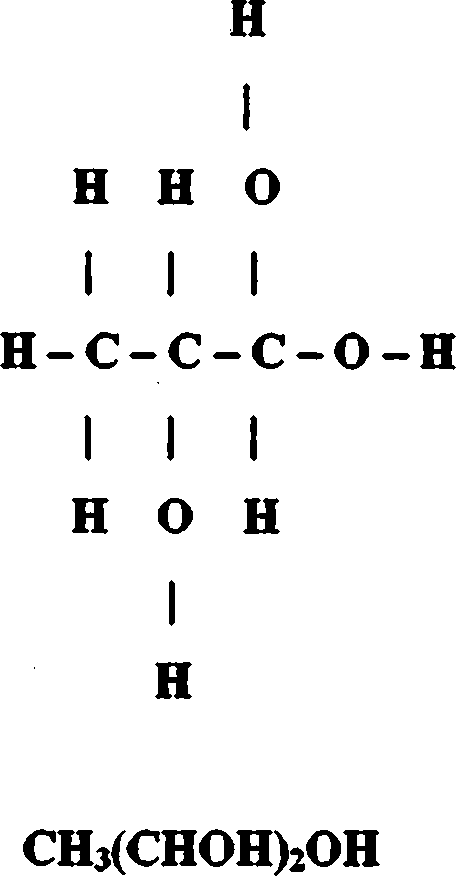
Struktura Pierwsza (R₁) Struktura Druga (R₂)

Korzystamy ze wzoru:

R₁ = 5·1,68∙10^-5 + 2·1,3∙10^-5 + 3·1,54∙10^-5 + 3·1,66∙10^-5 = 2,06∙10^-5 [m³/mol]

R₂ = 6·1,68∙10^-5 + 1·1,3∙10^-5 + 4·1,54∙10^-5 + 2·1,66∙10^-5 = 2,09∙10^-5 [m³/mol].

• Zestawiając wyniki refrakcji molowych doświadczalnej i teoretycznych:

|R_doś. - R₁| = |2,08557 ∙10^-5- 2,06∙10^-5| = 0,256 ∙10^-7[m³/mol];

|R_doś. - R₂| = |2,08557 ∙10^-5 - 2,09∙10^-5| = 0,443243 ∙10^-8[m³/mol].

Dla drugiej struktury otrzymaliśmy wynik prawie sześciokrotnie mniejszy.

Wyznaczanie momentu dipolowego wody destylowanej, etanolu i gliceryny.

• Wychodząc z teorii Debye'a zauważamy, że dla cząsteczek obdarzonych stałym momentem dipolowym µ zachodzi relacja:

,

ε - przenikalność dielektryczna danego materiału;

N_A - liczba Avogadra;

ε₀ - przenikalność dielektryczna próżni;

k - stała Boltzmana;

T - temperatura w skali bezwzględnej.

Po przekształceniu otrzymujemy wzór na obliczenie momentu dipolowego:

• Na podstawie tego wzoru wyznaczamy momenty dipolowe dla cząsteczki etanolu, gliceryny oraz wody destylowanej, korzystając przy tym z tabeli:

Cząsteczka	Przenikalność dielektryka ε	Moment dipolowy µtabl.[D]
Woda	81	1,84
Etanol	25,8	1,7
Gliceryna	40	2,8

Wartości momentów dipolowych należy podać w debajach:

1D = 1/3 ∙ 10^-27 [Cm].

• Moment dipolowy wody destylowanej (n=1, 1,332; ρ=1000 kg/m³; M=0,018 kg/mol):

μ = 0,274 ∙ 10^-29 [Cm] = 0,83 [D]

• Moment dipolowy etanolu (n= 1,3605; ρ=789,5 kg/m³; M=0,046 kg/mol):

μ = 0,459 ∙ 10^-29 [Cm] = 1,39 [D]

• Moment dipolowy gliceryny (n=1,471; ρ=1233 kg/m³; M=0,092 kg/mol):

μ = 0,51 ∙ 10^-29 [Cm] =1,545454545 [D]

• Porównanie otrzymanych wyników i wyników tablicowych:

Substancja	µdośw. [D]	µtabl. [D]	Różnica [D]
woda	0,83	1,84	1,01
etanol	1,39	1,7	0,31
gliceryna	1,545454545	2,8	1,254545455

Wnioski:

Współczynnik załamania światła rośnie ze wzrostem stężenia roztworu, lecz tylko do pewnego momentu - potem się stabilizuje i dochodząc do 100% maleje. Przedstawia to krzywa obrazująca zależność n = f(c) na wykresie. Znając wartość współczynnika załamania, można z owego wykresu odczytać stężenie roztworu danej substancji oraz metodą ekstrapolacji, odczytać nieznany współczynnik dla stężenia 100%.

Refrakcja molowa ściśle zależy od współczynnika załamania światła. Dzięki tym relacjom, przeprowadzając odpowiednie doświadczenia i obliczenia, jesteśmy w stanie dowieść, która z proponowanych struktur cząsteczki jest prawidłowa . Wyliczając refrakcję molową doświadczalną i teoretyczne refrakcje proponowanych wzorów etanolu i gliceryny, na podstawie egzaltacji refrakcji, otrzymujemy iż prawidłową strukturą dla etanolu jest struktura pierwsza, a dla gliceryny struktura druga. Dla etanolu wynik jest prawidłowy, natomiast jeśli chodzi o glicerynę to właściwą jest struktura pierwsza. Przyczyną niewłaściwego wyniku doświadczenia może być nieprecyzyjny pomiar współczynnika załamania.

Różnica pomiędzy refrakcją obliczoną a wyznaczoną doświadczalnie dla etanolu o stężeniu równym 40% wynosi 0,233∙10^-8. Można uznać, iż jest to różnica relatywnie mała potwierdzająca precyzje wykonanych pomiarów dla etanolu.

Z otrzymanych obliczeń wynika także, że dla mniejszych wartości współczynnika załamania światła (a co za tym idzie dla niższych stężeń), wartość refrakcji także jest mniejsza.

Współczynnik załamania światła jest ściśle związany ze stałym momentem dipolowym związków. Między wartościami momentów dipolowych wody, etanolu i gliceryny otrzymanych w wyniku obliczeń, ich wartościami tablicowymi istnieją znaczne różnice. Największa różnica między tymi wartościami występuje dla glukozy, najmniejsza zaś dla etanolu. Częściowo może to być wynikiem nie do końca precyzyjnych pomiarów współczynników załamania danych substancji. Na wynik wpływ ma także temperatura (poprzez zależność gęstości i współczynnika załamania od temperatury)

2

---