1. Czym zajmuje się statyka.

Statyka jest działem mechaniki zajmująca się przekształceniem oraz równowagą układów sił.
2. Co nazywamy układem sił.
Przez układ sił rozumiemy zbiór sił przyłożonych w jednym lub kilku punktach bryły. Najprostszym układem sił jest tzw. dwójka zerowa
3. Dokonać podział sił i ich układów.
-siły zewnętrzne
-siły wewnętrzne
Siły zewnętrzne- to siły przyłożone do poszczególnych brył układów pochodzące od brył nie wchodzących w skład rozpatrywanego układu.
Dzielimy je na 2 grupy:
-siły czynne mogące wykonać ruch układu
-siły reakcji pochodzące od więzów gdy układ jest nieswobodny
Siły wewnętrzne- są to siły z jakimi oddziaływają na siebie poszczególne bryły lub punkty materialne wchodzące w skład danego układu.
4. Podać brzmienie trzeciego prawa Newtona (dla dwóch brył).
Jeżeli punkt A bryły I działa na punkt B bryły II z siłą S₁₂ to punkt B bryły II oddziałuje na punkt A bryły I z siłą S₂₁ równą poprzedniej co do wartości, działającą wzdłuż tej samej prostej ale o zwrocie przeciwnym.
5. Na jakie grupy dzielimy więzy ograniczające swobodę ruch u ciała.
Połączenia (więzy) dzielimy dzielimy na następujące grupy:
- Liny, łańcuchy czyli tzn. cięgna - proste działania są znane i pokrywają się z kierunkiem cięgna.
- Podpory gładkie i przesuwne - prosta działania reakcji jest prostopadła do powierzchni podparcia
- Podpory chropowate i nieprzesuwne - proste działania reakcji są nieznane.
- Przeguby walcowe lub kuliste (połączenia pozwalające poruszać się jednej bryle w drugiej) - prosta działania reakcji przegubu jest nieznana.
- Utwierdzenia i zamocowania - prosta działania reakcji w ogólnym przypadku może być nieznana przy utwierdzeniu oprócz siły reakcji należy przyłożyć jeszcze tzn. moment utwierdzenia.
6. Jak działają reakcje w cięgnach. Zilustrować przykładami.


7. Jak działają reakcje w podporach gładkich - przesuwnych. Zilustrować przykładami.


8. Jak działają reakcje w podporach chropowatych - nieprzesuwnych. Zilustrować przykładami.
9. Jak działają reakcje w przegubach walcowych i kulistych. Zilustrować przykładami.

10. Jak działają reakcje w utwierdzeniach - zamocowaniach. Zilustrować przykładem.


11. Podać definicję twierdzenia o trzech siłach.

Trzy siły są w równowadze jeżeli ich proste działania przecinają się w jednym punkcie, leżą w jednej płaszczyźnie i trójkąt sił jest trójkątem zamkniętym.
12. Podać warunki równowagi płaskiego środkowego układu sił (definicja, zapis).
Układ sił, w którym proste działania przecinają się w jednym punkcie nazywamy układem środkowym.
Warunkiem koniecznym i wystarczającym równowagi płaskiego środkowego układu sił jest, aby algebraiczna sumy rzutów wszystkich sił na dwie osie prostokątnego układu odniesienia były równe zero.
Jeżeli wielobok jest zamknięty, to suma geometryczna jest równa zero, czyli
_g = 0 lub

Analityczny zapis warunku równowagi płaskiego środkowego układu sił
13. Podać warunki równowagi przestrzennego środkowego układu sił (definicja, zapis).
Warunkiem koniecznym i wystarczającym równowagi przestrzennego środkowego układu sił jest aby algebraiczna sumy rzutów wszystkich sił na trzy osie prostokątnego układu odniesienia były równe zero.

_g = 0 lub

Analityczny zapis warunku równowagi przestrzennego środkowego układu sił
14. Podać definicję momentu siły względem punktu (bieguna).

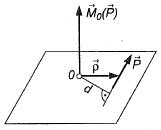
Moment siły względem punktu (bieguna) nazywamy wektor
₀(
taki, że:
₀(
=
x
.
Wektor ten jest więc prostopadły do wektorów
oraz
, a więc jest prostopadły do płaszczyzny wyznaczonej przez prostą działania siły i punkt. Wartość wektora siły jest równa: M₀
= Pd
d - ramię siły
d = ρ sin (
,
)


15. Podać definicję wektora głównego i momentu głównego (dla układu płaskiego sił).

Siła jest równa sumie wszystkich sił układu. Geometryczną sumę sił układu nazywamy wektorem główny oznaczamy zwykle symbolem Wg. Sumę algebraicznych momentów sił składowych względem bieguna redukcji nazywamy momentem głównym i oznaczamy
_g.



16. Podać warunki równowagi płaskiego dowolnego układu sił (definicja, zapis).
Warunkiem koniecznym i wystarczającym równowadze płaskiego dowolnego układu sił jest, aby sumy algebraiczne rzutów sił na każdą z dwóch nierównoległych osi równały się zeru oraz suma momentów sił względem dowolnie obranego bieguna na płaszczyźnie działania tych sił była równa zeru.


17. Podać warunki równowagi przestrzennego dowolnego układu sił (definicja, zapis).
Warunkiem koniecznym i wystarczającym równowadze przestrzennego dowolnego układu sił jest aby algebraiczne sumy rzutów wszystkich sił na trzy osie prostokątnego układu odniesienia były równe zeru oraz aby algebraiczne sumy momentów wszystkich sił względem tych trzech osi były równe zeru.
Przestrzenny dowolny układ pozostaje w równowadze, gdy:
_g = 0 i
_g = 0

18. Podać wzory na określenie współrzędnych środka ciężkości figury płaskiej.

F- pole figury płaskiej
19. Zdefiniować momenty statyczne figury płaskiej względem osi.
Momentem statycznym figury płaskiej względem dowolnej osi nazywamy iloczyn pola tej figury i współrzędnej środka ciężkości tej figury względem tej samej osi.
20. Czym zajmuje się wytrzymałość materiałów.
Wytrzymałość materiałów zajmuje się badaniem zjawisk występujących w ciałach rzeczywistych, to jest w ciałach odkształconych pod wpływem przyłożonych do nich obciążeń.
21. Jakie cztery warunki należy spełnić, aby poprawnie zaprojektować element konstrukcyjny z punktu widzenia wytrzymałości.
-warunek bezpieczeństwa
-warunek sztywności
-warunek styczność postaci
-warunek ekonomiczności konstrukcji
22. Co rozumiemy pod pojęciem sił zewnętrznych w wytrzymałości materiałów.
Pod pojęciem sił zewnętrznych rozumiemy siły czynne czyli obciążenia oraz siły bierne czyli reakcje. Zarówno obciążenia i reakcje działają na dane ciało z zewnątrz.
23. Co rozumiemy pod pojęciem sił wewnętrznych w wytrzymałości materiałów.
Siły wewnętrzne są to siły z jakimi oddziaływają na siebie cząstki wewnątrz ciała przeciwdziałając każdej zmianie odległości poszczególnych jego punktów (siły wewnętrzne możemy łatwo wyznaczyć metodą przecięć)
24. Podać trzy zasadnicze rodzaje obciążenia konstrukcji (w wytrzymałości materiałów).
W zależności od sposobu przyłożenia sił zewnętrznych rozróżniamy przypadki obciążeń: rozciąganie lub ściskanie, zginanie, skręcanie lub ścinanie.
25. Narysować wykres rozciągania dla stali miękkiej.
26. Podać prawo Hooke'a dla rozciągania, co to jest sztywność pręta na rozciąganie.
W przypadku prętów poddanych rozciąganiu lub ściskaniu jeżeli tylko wielkość siły nie przekroczy pewnej granicy to wydłużenie pręta jest wprost proporcjonalne do siły rozciągającej pręt i jego długości a odwrotnie proporcjonalne do przekroju pręta.

Δl=α
α- bardzo mała dlatego E =
dlatego Δl =

E*F - sztywność pręta przy rozciąganiu

27. Podać definicję momentu bezwładności figury płaskiej.
Momentem bezwładności J_z figury płaskiej o powierzchni F względem dowolnej osi leżącej w płaszczyźnie figury nazywamy sumę iloczynów elementarnych powierzchni dF figury i kwadratu ich odległości



Biegunowym momentem bezwładności figury płaskiej (przekroju) o powierzchni F względem dowolnego punktu O (bieguna) leżącego w płaszczyźnie figury nazywamy sumę iloczynów elementarnych powierzchni dF figury i kwadratu ich odległości od bieguna
J₀ =
dF
=
+
stąd J₀ =
dF =
dF +
dF czyli J_o = J_z + J_y


28. Podać wzór Steinera (dołączyć ilustrację graficzną).

Wzór: Iż = I_zc = a²F

29. Podać warunek wytrzymałości elementu rozciąganego.
ϭ_r≤ k_r rozciąganie ϭ- naprężenie rozciągania ; k_r naprężenie krzywienia.
30. Podać warunek wytrzymałości elementu ścinanego.

_t≤ k_t ścinanie

31. Podać warunek wytrzymałości elementu skręcanego.

_s≤ k_s skręcanie.

32. Podać warunek wytrzymałości elementu zginanego.
ϭ_g≤k_g zginanie
- naprężenie styczne =
; ϭ - naprężenie

36. Warstwa obojętna belki.

Warstwa obojętna belki jest to warstwa wewnątrz materiału, która nie jest ani rozciągana ani ściskana. W prostych belkach warstwa obojętna przechodzi przez środki ciężkości przekrojów.
47. Czym zajmuje się kinematyka, podział kinematyki.
Kinematyka jest to dział mechaniki zajmujący się badaniem ruchu ciał bez uwzględniania sił powodujących ten ruch. Kinematykę dzielimy na:
- kinematykę punktu
- kinematykę ciała sztywnego.
48. Wymień sposoby opisania ruchu punktu.
Istnieje kilka sposobów opisu ruchu punktu:
1)  przez podanie wektora - promienia wodzącego punkt ruchomy w funkcji czasu,
2)  przez podanie współrzędnych kartezjańskich jako funkcji czasu, czyli tak zwanych równań
     skończonych ruchu,
3)  przez podanie toru i współrzędnej krzywoliniowej wzdłuż toru, okreŚlającej sposób poruszania się
     po torze,
4)  przez podanie innych współrzędnych krzywoliniowych jako funkcji czasu np: biegunowych,
     walcowych, sferycznych.
49. Przyśpieszenie punktu w ruchu krzywoliniowym.
Przyśpieszenie punktu jest równe pierwszej pochodnej prędkości lub drugiej pochodnej położenia względem czasu.
50. Podać klasyfikację ruchu punktu ze względu na tor.
- ruch prostoliniowy
- ruch krzywoliniowy (płaski lub przestrzenny)
51. Podać klasyfikację ruchu punktu ze względu na sposób poruszania się po torze.
- jednostajny

- jednostajnie zmienny

- ruch zmienny

- ruch okresowy
52. Podać klasyfikację ruchów brył.
- postępowy
- obrotowy

- płaski

- kulisty

- dowolny
53. Zapisać związek między prędkością obrotową, a prędkością kątową.
Prędkość obrotowa - liczba obrotów dowolnego układu obrotowego wykonana w dowolnej jednostce czasu. Zależność:

54. Jak wyznaczamy przyśpieszenie styczne i normalne punktów w ruchu obrotowym.
55. Omówić własności przyspieszenia Coriolisa.
Przyspieszenie Coriolisa jest podwójnym iloczynem wektorowym prędkości kątowej i prędkości względnej. To przyspieszenie występuje w geometrycznej sumie przyspieszenia bezwzględnego punktu.
56. Podać definicję ruchu płaskiego bryły.

Jeżeli wszystkie punktu bryły poruszają się w płaszczyznach równoległych do pewnej płaszczyzny nieruchomej, to ruch bryły jest ruchem płaskim.
57. Czym zajmuje się dynamika.
Dynamika jest działem mechaniki zajmująca się badaniem ruchu ciał pod wpływem działa sił. Zajmuje się przyczynami i skutkami ruchów oraz ustala zależność między ruchem ciał a siłami oddziałującymi na nie.
58. Podać definicję drugiego prawa Newtona.

Przyspieszenie punktu materialnego jest proporcjonalne do siły działającej na ten punkt i na kierunek tej siły:
= m

59. Wymienić dwa podstawowe zadania dynamiki punktu (na czym polega rozwiązywanie obu zadań).
- zadania proste (pierwsze) - polegają na wyznaczeniu sił działających na punkt materialny, którego ruch jest znany
- zadanie odwrotne (drugie) - polegają na określeniu ruchu punktu materialnego, gdy znane są siły działające na niego.
60. Zdefiniować pracę stałej siły na przesunięciu prostoliniowym. Podać jednostkę pracy.
Praca stała co do wartości siły na przesunięciu prostoliniowym jest to iloczyn skalarny wektora siły i wektora przesunięcia punktu jej przyłożenia. L =

[ Nm ]
61. Podać definicje sprawności mechanicznej.
Sprawność mechaniczna (moc siły) - jest to zmiana pracy siły, odniesiona w jednostce czasu. Wyrażamy wzorem: N =


62. Podać wzór na energię kinetyczna ciała w ruchu postępowym.


63. Podać wzór na energię kinetyczną ciała w ruchu obrotowym.


64. Co nazywamy energią mechaniczną. Jak brzmi zasada zachowania energii mechanicznej.
Energią mechaniczną nazywamy geometryczna sumę energii kinetycznej i potencjalnej.
Zasada zachowania energii mówi, że suma energii kinetycznej i potencjalnej w polu potencjalnym jest wielkością stałą.

---