Ruch drgający

• Drganie (ruch drgający) - ruch (lub zmiana stanu), który charakteryzuje się powtarzalnością w czasie wielkości fizycznych, określających ten ruch lub stan (np. położenie, prędkość).

• Drganie okresowe (periodyczne) - powtarzanie zachodzi zawsze po tym samym czasie
, zwanym okresem.

• Drganie okresowe harmoniczne - położenie ciała opisuje funkcja sinus (bądź kosinus):

• W ruchu harmonicznym:

Prędkość

Przyspieszenie

Drgania harmoniczne

• Przypomnienie:

Druga zasada dynamiki Newtona:

• Ruch harmoniczny to taki, dla którego:

Siła jest proporcjonalna do wychylenia i przeciwnie do niego skierowana (prawo Hooke'a). (F - siła harmoniczna)

• Ogólne równanie różniczkowe drgań harmonicznych:

• Wykładniczy sposób zapisu drgań harmonicznych:

Drgania harmoniczne - c.d.

• Wielkości opisujące ruch harmoniczny prosty (drgania harmoniczne):

-
jest amplitudą drgań (maksymalną zmianą względem położenia równowagi);

-
to faza drgań (mierzona w radianach bądź stopniach);

-
to częstość kołowa (pulsacja) (w radianach na sekundę);

-
to faza początkowa.

- Częstotliwość drgań:
(Hz - herc);

Drgania harmoniczne - przykłady

• Wahadło matematyczne:

Punkt materialny, zawieszony na nieważkiej i nierozciągliwej nici;

;
;

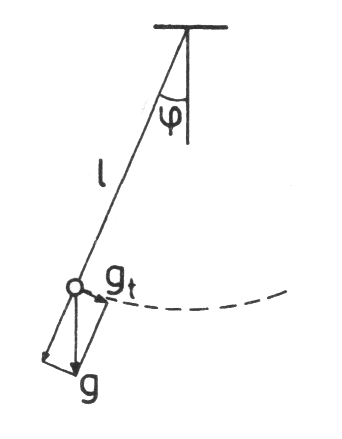
• Wahadło fizyczne:

Ciało doskonale sztywne, które pod działaniem własnego ciężaru waha się dookoła osi poziomej, nie przechodzącej przez środek ciężkości ciała;

Drgania harmoniczne - przykłady - c.d.

• Sprężyna:

• Obwód LC:

;
;

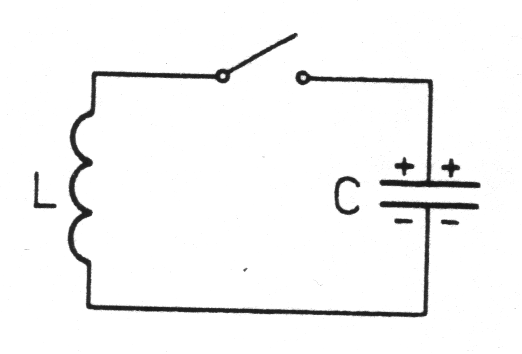
Składanie drgań harmonicznych

• Zasada superpozycji: Jeżeli ciało podlega jednocześnie dwóm drganiom, to jego wychylenie jest sumą wychyleń, wynikających z każdego ruchu.

• Składanie drgań harmonicznych, odbywających się wzdłuż jednej prostej:

• Przypadek dwóch ruchów harmonicznych, odbywających się z jednakową częstością
  : wypadkowa jest drganiem z tą samą częstością!

=>

gdzie:

- amplituda

- faza

Składanie drgań harmonicznych - c.d.¹

• Amplituda drgania wypadkowego zależy od różnicy początkowych faz
drgań składowych. Jeśli ta różnica nie zmienia się z upływem czasu, to takie drgania synchroniczne nazywamy koherentnymi.

Przypadki szczególne:

1. Różnica faz drgań składowych równa się zeru albo całkowitej wielokrotności 2π:

Maksymalna amplituda drgań jest sumą amplitud drgań składowych.

2. Różnica faz drgań składowych równa się nieparzystej wielokrotności π:

Maksymalna amplituda drgań jest różnicą amplitud drgań składowych.

Składanie drgań harmonicznych - c.d.²

• Przypadek dwóch ruchów harmonicznych, odbywających się z różną częstotliwością: wypadkowa jest prostym drganiem harmonicznym tylko wtedy, gdy stosunek obu częstotliwości można wyrazić liczba wymierną.

• Przypadek dwóch ruchów harmonicznych (o jednakowej amplitudzie), których częstości różnią się nieznacznie: dudnienia:

Składanie drgań harmonicznych - c.d.³

• Jeśli różnica faz
drgań składowych zmienia się z upływem czasu w sposób dowolny, to amplituda drgań wypadkowych zmienia się z upływem czasu i nie ma sensu w ogóle mówić o składaniu amplitud. Jest to tzw. niekoherentne składanie drgań.

• Drgania typu:

nazywamy modulowanymi.

1) modulowana faza (częstość) - FM:

,

2) modulowana amplituda - AM:

,

Analiza harmoniczna

• Analiza harmoniczna - to sposób na przedstawienie złożonych drgań modulowanych w postaci szeregu prostych drgań harmonicznych.

• G. Fourier: dowolne drganie złożone można przedstawić jako sumę prostych drgań harmonicznych o wielokrotnościach pewnej podstawowej częstości kątowej
:

W ogólnym przypadku, liczba wyrazów w szeregu Fouriera jest nieskończona (możemy wtedy przejść do całek zamiast sum), ale istnieją takie drgania, dla których szeregi Fouriera nie zawierają pewnych wyrazów.

Składanie prostopadłych drgań harmonicznych

• Załóżmy, że punkt materialny uczestniczy jednocześnie w dwóch drganiach harmonicznych, odbywających się z jednakowymi częstościami
w dwóch kierunkach wzajemnie prostopadłych:

1. Początkowe fazy obu drgań są jednakowe:

Można tak ustawić odczyt czasu, żeby były równe zeru:

Dzieląc stronami:
- linia prosta

2. Początkowa różnica faz obu drgań jest równa
   :

Wtedy:
- linia prosta

Składanie prostopadłych drgań harmonicznych

3. Początkowa różnica faz obu drgań jest równa
   :

Wtedy:

i ostatecznie:
- elipsa

Punkt porusza się po tej elipsie przeciwnie do ruchu wskazówek zegara;

4. Początkowa różnica faz obu drgań jest równa
   :

- również elipsa, ale o obiegu zgodnym z ruchem wskazówek zegara;

5. Inne różnice faz

- również elipsy, ale o osiach nie pokrywających się z osiami układu współrzędnych.

• W przypadku ogólnym - dowolne częstości, amplitudy, fazy - mamy do czynienia z tzw. figurami Lissajous.

Drgania tłumione (gasnące)

• Siły oporu (tarcia) są zwykle proporcjonalne do prędkości ciała:

• Oscylator mechaniczny w obecności sił tarcia (tłumienie):

• Obwód RLC (opór R odpowiada za tłumienie):

• Ogólne równanie drgań tłumionych (straty energii na oporze ośrodka, proporcjonalne do pierwszej pochodnej zmiany położenia):

(dla oscylatora mechanicznego:
,
)

Drgania tłumione (gasnące) - c.d.¹

• Ogólne rozwiązanie w postaci kombinacji liniowej rozwiązań szczegółowych:

gdzie:

Rodzaje rozwiązań:

1. dla
   oba pierwiastki są rzeczywiste i ujemne, więc rozwiązaniem jest aperiodyczne, wykładnicze malenie x od A do zera;

2. dla
   występuje tzw. tłumienie krytyczne - jest to minimalna wartość tłumienia, przy której ruch jest aperiodyczny;

3. dla
   mamy drgania gasnące - oscylacje o zanikającej amplitudzie:

Drgania tłumione (gasnące) - c.d.²

• Ograniczając się do jednego rozwiązania (znak „plus” przy fazie) i pisząc rozwiązanie w postaci funkcji harmonicznej:

-
nazywamy amplitudą drgań gasnących;

-
to współczynnik tłumienia;

-
to częstość własna drgań układu tłumionego;

-
to częstość drgań swobodnych układu;

Drgania tłumione (gasnące) - c.d.³

• Drgania gasnące są drganiami nieokreślonymi - nigdy nie powtarzają się największe wartości wychylenia, prędkości, przyspieszenia. Dlatego
tylko umownie można nazwać częstością kątową - w tym sensie, że wskazuje ona, ile razy w ciągu
sekund drgający układ przechodzi przez położenie równowagi!

• Podobnie:

nazwiemy umownym okresem drgań gasnących.

Drgania tłumione (gasnące) - c.d.⁴

• Współczynnik tłumienia:
mówi nam o stosunku kolejnych amplitud drgań gasnących:

• Naturalny logarytm stosunku amplitud dwóch kolejnych wychyleń, następujących po sobie w odstępie czasu
(umownego okresu) nazywamy dekrementem logarytmicznym tłumienia
:

Drgania tłumione (gasnące) - c.d.⁵

• Oznaczmy przez
odstęp czasu, w ciągu którego amplituda drgań zmniejszy się
-krotnie. Wtedy:

albo:

czyli: współczynnik tłumienia
jest wielkością fizyczną równą odwrotności odstępu czasu
, w ciągu którego amplituda zmniejsza się
-razy. Czas
nazywamy czasem relaksacji.

• Podobnie: gdy przez
oznaczymy liczbę drgań, po wykonaniu których amplituda zmaleje
-razy, okaże się, że:

czyli: dekrement logarytmiczny tłumienia
jest wielkością równą odwrotności liczby drgań, po upływie których amplituda zmniejszy się
-razy.

Drgania wymuszone

• Oprócz siły sprężystej i siły oporu, działamy na układ dodatkową siłą - okresową siłą wymuszającą
:

• Ogólne równanie ruchu oscylatora mechanicznego przybiera wtedy postać:

• Spodziewamy się rozwiązania powyższego równania różniczkowego w postaci drgania harmonicznego z częstością
, równą częstości siły wymuszającej
, ale amplituda tych drgań powinna „zawierać informacje” o masie
, tłumieniu
i wielkości siły wymuszającej
a także częstości własnej
układu:

Drgania wymuszone - c.d.¹

• Można pokazać, że:

Amplituda
ustalonych drgań wymuszonych jest wprost proporcjonalna do amplitudy siły wymuszającej
i odwrotnie proporcjonalna do masy
układu oraz zmniejsza się wraz ze wzrostem współczynnika tłumienia
.

• „Faza początkowa”
ma teraz sens różnicy faz między amplitudą drgań wymuszonych
i amplitudą siły wymuszającej
(ściślej: ponieważ użyliśmy funkcji „cosinus” do opisu siły wymuszającej i funkcji „sinus” do opisu drgania
, to szukaną różnicą faz będzie:
):

Drgania wymuszone - c.d.²

• Analizując wyrażenie na amplitudę drgań wymuszonych:

możemy zauważyć, że w przypadku braku tłumienia
, gdy częstość
siły wymuszającej
równa jest częstości drgań własnych
układu, amplituda ta rośnie do nieskończoności!

Natomiast w obecności tłumienia
, maksimum wyrażenia na amplitudę
uzyskamy dla:

Zjawisko to nazywamy

rezonansem.

Drgania wymuszone - c.d.³

• Przykład obwodu elektrycznego: siła elektromotoryczna, wymuszająca drgania, jest równa:

Wtedy: równanie opisujące ruch ładunku elektrycznego w obwodzie (prąd elektryczny!):

Rozwiązanie ogólne w postaci:

gdzie:

i:

21

x

---