|
Akademia Górniczo - Hutnicza W Krakowie |
Wykonał: Dariusz Krakowski |
|||||||
KATEDRA AUTOMATYKI , NAPĘDU I URZĄDZEŃ PRZEMYSŁOWYCH AGH |
|||||||||
Wydział: EAIiE |
Rok akad.: 1998 / 99 |
Rok studiów: II |
Kierunek: Elektrotechnika |
Grupa: 3 |
|||||
Temat ćwiczenia: Regulator PID- charakterystyki czasowe i częstotliwościowe. |
|||||||||
Data wykonania: |
Data zaliczenia: |
Ocena: |
|||||||
Wprowadzenie teoretyczne
Regulator PID jest elementem układu regulacji realizującym w przypadku idealnym następującą zależność u(t) od e(t) :
Odpowiada to transmitancji:
gdzie:
Kp - współczynnik wzmocnienia proporcjonalnego
Ki - współczynnik wzmocnienia całkowego
Kd - współczynnik wzmocnienia różniczkowego
- inercja rzędu 0,001
Ki = 1/Ti
Kd = Td
Ti - czas zdwojenia
Td - czas wyprzedzenia
Zadanie
Dobrać parametry regulatora PID według metody Ziglera i Nicholsa. Skorzystać z funkcji [Km, Pm, wcg, wcp] = margin (L, M) obliczając margines (zapas) wzmocnienia Km i fazy Pm dla układu opisanego równaniami stanu lub transmitancją (L - licznik, M - mianownik) oraz odpowiadające im częstotliwości graniczne - odpowiednio wcg (= w180) i wcp. Przedstawić przebiegi.
Obiekt:
.
H(s)=1 - pętla jednostkowego sprzężenia zwrotnego
D(s)=0 - sygnał zakłócenia
Otrzymane wartości (nastawy regulatora PID)
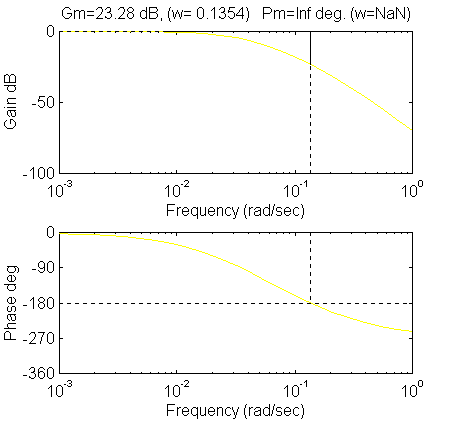
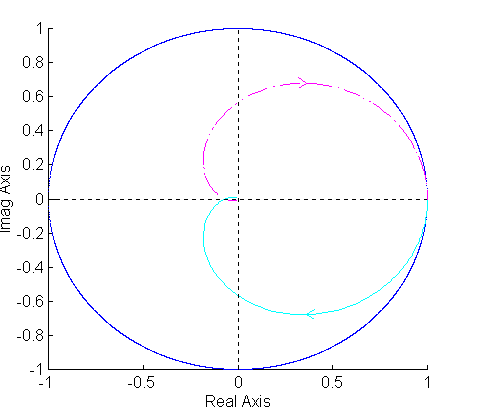
Charakterystyki Bode'go i NyquistaPrzebiegi y(t) dla poniższego schematu.
regulator P
regulator PD:
regulator PI:
regulator PID:
Wykresy otrzymane w symulacji.
Wpływ zmian nastaw na parametry układu (dla malejących nastaw kP,kD,kI.)
Wnioski
Kp : poprawia parametry badanego układu, powodując szybsze osiągnięcie wartości ustalonej przez układ. Niestety zbyt duży wzrost zadanego parametru powoduje powstawanie oscylacji. Parametr ten należy dobierać w ten sposób, aby uzyskać kompromis pomiędzy szybkością narastania sygnału i brakiem oscylacji a szerokością pasma.
Ki : powoduje poprawę działania układu. Zmiana tego parametru wpływa podobnie na działanie układu jak zmiana Kp, jednak zmiana Ki dokonuje się w o wiele mniejszym przedziale. Także w przypadku wzrostu tego parametru sygnał szybciej ustala się na danej wartości.
Kd : powoduje nieznaczny wzrost szybkości narastania obserwowanego sygnału. W zakresie dokonanych zmian nie da się zauważyć żadnych przeregulowań.
Km |
wcg |
||||
14.5833 |
0.1354 |
||||
Kp |
Ti |
Ki |
Td |
Kd |
|
8.7500 |
23.2022 |
0.0431 |
5.8005 |
5.8005 |
|
Na podstawie tych dwóch charakterystyk możemy stwierdzić, że występuje zapas amplitudy - układ stabilny, natomiast zapas fazy jest już trudniej określić ponieważ wykresy stykają się przy częstotliwości zero(rysunek prawy), a więc przy każdym obrocie fazy o 360 stopni. W takiej sytuacji możemy na pewno stwierdzić, że układ jest stabilny.
dla d(t) = 1(t) i ref(t) = 0 transmitancja układu wynosi:
dla d(t) = 0 i ref(t) = 1(t) transmitancja układu wynosi:
dla d(t) = 1(t) i ref(t) = 0 transmitancja układu wynosi:
dla d(t) = 0 i ref(t) = 1(t) transmitancja układu wynosi:
dla d(t) = 1(t) i ref(t) = 0 transmitancja układu wynosi:
dla d(t) = 0 i ref(t) = 1(t) transmitancja układu wynosi:
dla d(t) = 1(t) i ref(t) = 0 transmitancja układu wynosi:
dla d(t) = 0 i ref(t) = 1(t) transmitancja układu wynosi:
dla regulatora „P”
dla d(t)=1(t),ref(t)=0 dla d(t)=0,ref(t)=1(t)
dla regulatora „PI”
dla d(t)=1(t),ref(t)=0 dla d(t)=0,ref(t)=1(t)
dla regulatora „PID”
dla d(t)=1(t),ref(t)=0 dla d(t)=0,ref(t)=1(t)
Na podstawie wykresów, gdzie wymuszeniem jest sygnał zakłócenia, możemy określić czy dany regulator wprowadza uchyb. Dla PID i PI maleje on do zera natomiast dla P ustala się na konkretnej wartości. Gdy zakłócenie jest równe zero obserwujemy jakościowe możliwości regulacyjne regulatorów:
P |
wprowadza uchyb, małe przeregulowanie i mała ilość oscylacji |
PI |
brak uchybu, największe przeregulowanie i najwięcej oscylacji |
PID |
brak uchybu, średnie przeregulowanie i średnia ilość oscylacji |
|
Czas Narastania |
Przeregulowanie |
Czas ustalenia |
Błąd w stanie ustalonym |
Szerokość pasma |
Moduł rezonansowy |
Częstotliwość rezonansowa |
kP |
Narasta |
narasta |
narasta |
zmienia się |
stała |
narasta |
maleje |
kI |
Narasta |
opada |
zmienia się |
opada |
narasta |
opada |
zmienia się |
kD |
Narasta |
narasta |
narasta |
opada |
stała |
narasta |
zmienia się |
Zmiana parametru:
Wyszukiwarka
Podobne podstrony:
charakterystyki czasowe i czestotliwosciowe
Cw 2 charakt czasowe czestotliw
Pomiar charakterystyk czasowych i częstotliwościowych elementów automatyki, Semestr III, PA, przykla
Pomiar charakterystyk czasowych i częstotliwościowych elementów automatyki a, Semestr III, PA, przyk
Charakterystyki czasowe JG
REGULACJA PID , Energetyka, sem5, sem5, met.ZN
lab 1 pomiar charakter czasowych i cz stot
charakter czasowe nawigacja
BADANIE STATYCZNYCH I DYNAMICZNYCH WŁAŚCIWOŚCI REGULATORÓW PID
04Nastawy regulatora PID
REGULATOR PID, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
Badanie układu sterowania z regulatorem PID
Regulator PID Cool
Regulator PID (2)
DOBÓR NASTAW REGULATORA PID
2 Charakterystyki Czasowe
automaty-sprawko-pid, Temat ćwiczenia: REGULATORY PID
Regulator Pid
więcej podobnych podstron