Wyniki pomiarów:

Tabela 1. Przewodnictwo roztworu wzorcowego KCl

Stężenie roztworu KCl [M]	Temperatura [°C]	Przewodnictwo roztworu KCl L, [mS]				Stała naczyńka k [m^-1]	Stała naczyńka kśrednia [m^-1]
				L1KCl	L2KCl			L3KCl	LKCl średnia
0,1	18	10,65	10,79	10,70	10,71	104,5		96,3
0,01	18	1,403	1,376	1,38	1,39	88,1

Obliczenia:

1. stała naczyńka pomiarowego:
   

Tabela 2. Przewodnictwo badanego roztworu

Dane w tabeli zawierają średnią wartość przewodnictwa roztworu SDS, wyliczoną z trzech pomiarów.

Objętość dodanego roztworu SDS - V [cm^3]	Przewodnictwo roztworu SDS - Ls [μS]	Stężenie roztworu SDS - Cs [mol/m^3]	Przewodnictwo właściwe roztworu SDS - ks [S/m]	Przewodnictwo molowe roztworu SDS - Λ[S*m^2/mol]
0	1,7	0	0,0001637	0
1	26,6	0,331	0,0025616	0,0077360
2	48,9	0,658	0,0047091	0,0071578
3	71,9	0,98	0,0069240	0,0070624
4	95	1,299	0,0091485	0,0070443
5	117,8	1,613	0,0113441	0,0070334
6	140,2	1,923	0,0135013	0,0070207
7	161,2	2,229	0,0155236	0,0069634
8	184,5	2,532	0,0177674	0,0070181
9	204,7	2,83	0,0197126	0,0069651
10	225,7	3,125	0,0217349	0,0069552
11	246,3	3,416	0,0237187	0,0069431
12	267	3,704	0,0257121	0,0069423
13	287,3	3,988	0,0276670	0,0069380
14	306,7	4,268	0,0295352	0,0069197
15	326,7	4,545	0,0314612	0,0069215
16	346	4,819	0,0333198	0,0069139
17	365,7	5,09	0,0352169	0,0069191
18	384	5,357	0,0369792	0,0069028
19	403	5,621	0,0388089	0,0069039
20	420,7	5,882	0,0405134	0,0068873
21	439,7	6,14	0,0423431	0,0068959
22	457,7	6,395	0,0440765	0,0068920
23	475	6,647	0,0457425	0,0068813
24	493	6,896	0,0474759	0,0068840
25	509,3	7,143	0,0490456	0,0068664
26	524,7	7,386	0,0505286	0,0068408
27	539	7,627	0,0519057	0,0068054
28	553,3	7,865	0,0532828	0,0067745
29	567,7	8,101	0,0546695	0,0067489
30	578	8,333	0,0556614	0,0066794
31	588	8,564	0,0566244	0,0066123
32	596,7	8,791	0,0574622	0,0065363
33	606	9,016	0,0583578	0,0064724
34	613,3	9,239	0,0590608	0,0063925
35	620,7	9,459	0,0597734	0,0063189
36	627,3	9,677	0,0604090	0,0062423
37	635,3	9,893	0,0611794	0,0061841
38	641,7	10,106	0,0617957	0,0061145
39	648,3	10,317	0,0624313	0,0060510
40	655	10,526	0,0630765	0,0059923
41	660,7	10,733	0,0636254	0,0059280
42	663,7	10,938	0,0639143	0,0058436
43	672,7	11,14	0,0647810	0,0058152
44	678,7	11,34	0,0653588	0,0057635
45	685,3	11,538	0,0659944	0,0057195

2. stężenie surfaktanta:
   , gdzie C₀=0,05 mo/dm³= 50 mol/m³

3. przewodnictwo właściwe:
   

4. przewodnictwo molowe:
   

Opracowanie wyników:

Wzrost stężenia surfaktanta w roztworze powoduje wzrost przewodnictwa właściwego

i jednocześnie spadek przewodnictwa molowego badanego roztworu. Wzrost przewodnictwa właściwego zależy od ilości jonów obecnych w roztworze, im większe stężenie surfaktanta, tym większa będzie liczba jonów zdolnych do przenoszenia prądu elektrycznego. Wzrost stężenia dodawanej substancji powoduje jednak zmniejszenie ruchliwości jonów, a co za tym idzie zmniejszenie przewodnictwa molowego roztworu.

Wyznaczenie CMC:

Zgodnie z równaniami dwóch prostych, punkt przecięcia prostych jest punktem Krytycznego Stężenia micelizacji.

CMC= 8,11 mol/m³

CMC_literaturowe= 8,30

Otrzymany wynik różni się od wartości literaturowej o 0,19. Na błąd pomiaru może wpływać niedokładne miareczkowanie ilości surfaktanta bądź zbyt szybkie odczytywanie wartości wskazywanych przez konduktometr.

Obliczenie stopnia jonizacji surfaktanta α:

constans1 = 0,0098

constans2 = 0,007

constans2=α∙constans1

α=

Obliczanie wartości standardowej entalpii swobodnej micelizacji

β=1 - α = 1 - 0,82 = 0,18

ΔG_M = RT(1+β)ln[CMC] = 8,314* (18+273)*(1+0,18)ln[0,00794]= - 13805,66 [

Ujemna wartość standardowej entalpii swobodnej świadczy o samorzutności procesu micelizacji.

Jeżeli natomiast rozpatrujemy poszczególne funkcje termodynamiczne micelizacji, wiemy, że dla danego surfaktantu powyżej stężenia krytycznego proces micelizacji jest procesem samorzutnym. W takiej sytuacji wartość ΔGM musi być mniejsza od zera. W przypadku entalpii micelizacji ΔHM, trudno na podstawie apriorycznych rozważań określić jej znak. Z pomiarów doświadczalnych wiadomo jednak, że proces micelizacji jest zazwyczaj procesem endotermicznym (ΔHM>0). Wiedząc, że ΔGM<0 i ΔHM>0 łatwo możemy określić znak entropii micelizacji ΔSM. Ponieważ z równania Gibasa-Helmholtza mamy: ΔGM=ΔHM - TΔSM<0, stąd TΔSM>ΔHM, a więc ΔSM musi być większa od zera (ponieważ T>0).

Entropia micelizacji ma wartość dodatnią, gdyż wartość entropii układu micelarnego jest większa niż roztworu doskonałego (nie micelarnego). Opisywane tu zjawisko przyciągania się grup hydrofobowych związane ze zwiększaniem się entropii rozpuszczalnika polarnego nazywane jest oddziaływaniem hydrofobowym.

Oddziaływania hydrofobowe - polegają na łączeniu się grup hydrofobowych, w celu ochrony cząsteczki przed oddziaływaniem na nie cząsteczek wody. Oddziaływanie to odpycha cząsteczki wody. Jest to bardzo szczególne oddziaływanie, ponieważ najczęściej rozpuszczalnikiem jest woda.

Standardowa entalpia swobodna tworzenia miceli ΔGM jest parametrem termodynamicznym charakteryzującym dany surfaktant i jest ściśle powiązana z wartością CMC. Dla roztworu doskonałego surfaktantu jego potencjał chemiczny zmienia się logarytmicznie ze stężeniem, co wyrażone jest równaniem (na rysunku linia przerywana):

μ = μ₀ + RT ln c

gdzie μ₀ - standardowy potencjał chemiczny surfaktantu w danym rozpuszczalniku, R - stała gazowa, T - temperatura wyrażona w K, c - stężenie molowe surfaktantu tworzącego roztwór doskonały.

Zależność potencjału chemicznego surfaktantu od stężenia: linia przerywana - roztwór doskonały, linia ciągła - układ rzeczywisty.

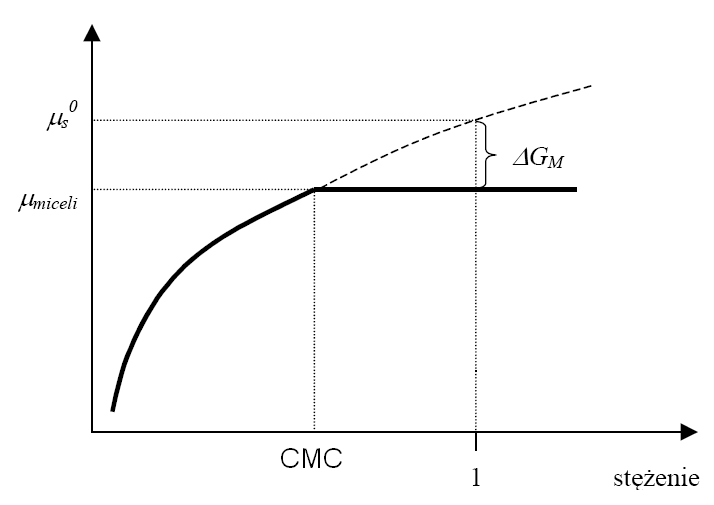
ΔGM = RT ln CMC równanie to spełnione jest dla miceli z surfaktantów niejonowych.

Dla surfaktantów jonowych równanie to przyjmuje postać: ΔGM = RT(1+β) ln CMC

gdzie β oznacza procent ładunku miceli zneutralizowanego przez przeciwjony z roztworu (w przypadku surfaktantu anionowego przeciwjonami są kationy, a w przypadku kationowego - aniony).

Wnioski:

Celem powyższego ćwiczenia było wyznaczenie krytycznego stężenia micelizacji. Jak wynika z otrzymanych wykresu zależność przewodnictwa właściwego od stężenia jest zależnością liniową. Zależność przewodnictwa molowego od stężenia jest zależnością bardziej złożoną. Przewodnictwo molowe w zakresie niskich stężeń maleje, następnie utrzymuje się na stałym poziomie, a w zakresie wysokich stężeń znowu zaczyna maleć. Zjawisko to jest spowodowane powstawaniem miceli. Źródłem błędów uzyskanych wyników może być niedokładne wyznaczenie stałej naczyńka konduktometrycznego oraz niedokładne sporządzenie r-rów.

4

---