Opis teoretyczny.

1. Rola indukcji, pojemności i oporu w obwodach prądu zmiennego.

W analizie obwodów elektrycznych przyjmuje się, że elementy R, L, C są idealizowanymi liniowymi modelami matematycznymi fizycznych elementów obwodu. Elementy te traktowane indywidualnie charakteryzują się następującymi właściwościami:

• R - rozpraszanie (dyssypacja) energii elektrycznej

• L - magazynowanie energii pola magnetycznego

• C - magazynowanie energii pola elektrycznego

Elementy R, L, C są nazywane idealnymi w tym sensie, ze każdy jest całkowicie wolny od właściwości dwóch pozostałych oraz że zależność między napięciem na ich zaciskach a prądem jest liniowa. Oznacza to, że zależność
jest opisana przez linowe równania różniczkowe oraz że współczynniki tych równań są stałe. R, L, C są stałymi obwodu, ich wartość jest niezależna od pulsacji oraz od amplitudy prądu lub napięcia.

Elementy rzeczywiste można przedstawić za pomocą schematów zastępczych, w których występują połączenia elementów idealnych, tak np. cewkę przy niezbyt wielkich częstotliwościach można przedstawić jako szeregowe połączenie idealnej rezystancji R i idealnej indukcyjności L.

Rozpatrzę teraz wpływ elementów R, L, C na przebiegi prądowo napięciowe przy przyłączeniu ich do źródła napięcia sinusoidalnego.

Opornik idealny.

Jeżeli do zacisków o napięciu
zostanie włączony opornik idealny (rysunek 1a), to zgodnie z prawem Ohma w obwodzie popłynie prąd:

(1)
,

który ma tę samą fazę co wywołujące go napięcie. Amplituda prądu wynosi
, zaś wartość skuteczna
.

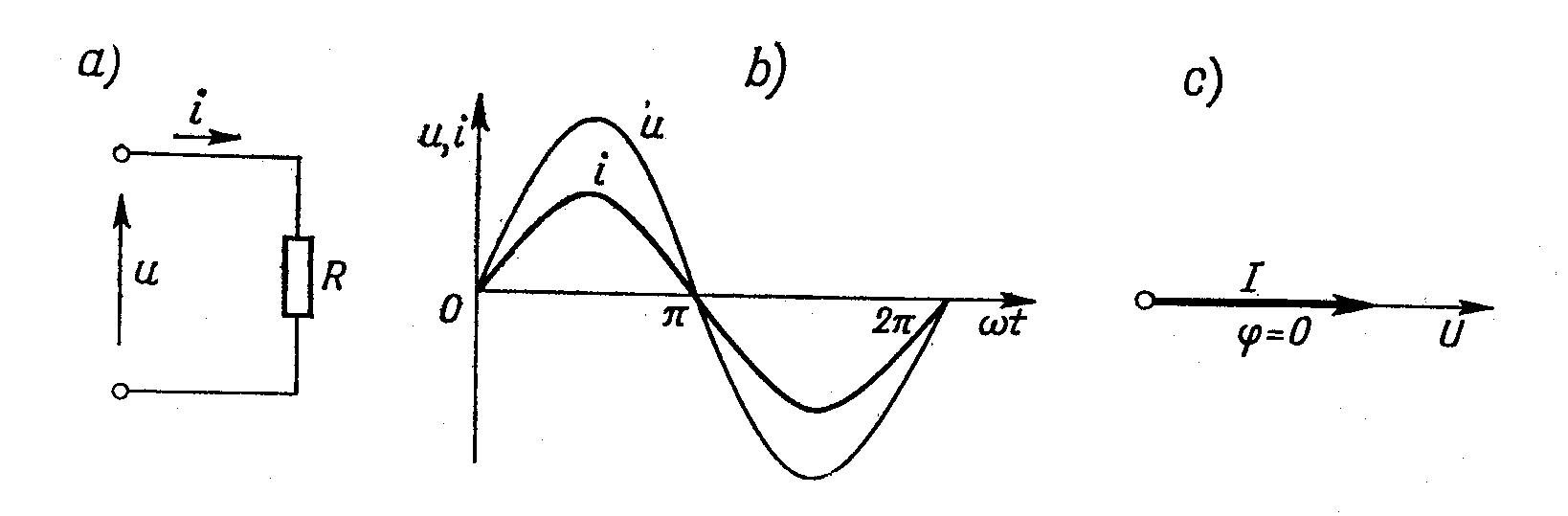
Rysunek 1

Powyższy rysunek przedstawia opornik idealny w sieci prądu sinusoidalnego. Poszczególne podpunkty są to:

1. schemat połączeń

2. wykres czasowy napięcia i prądu

3. wykres wektorowy

Jak widać z rysunku wektory
i
mają te same zwroty. Iloczyn
nazywa się napięciem czynnym i równa się ono napięciu przyłożonemu na zaciski opornika.

Cewka idealna.

Jeżeli do zacisków o chwilowej wartości napięcia
(rysunek 2) zostanie włączona idealna cewka, to popłynie przez nią prąd, którego zmiana w czasie spowoduje indukowanie się na zaciskach cewki siły elektromotorycznej samoindukcji:

(2)
.

Niech prąd płynący przez cewkę będzie równy:

(3)
.

Ponieważ na zaciskach cewki
, to:

(4)

Gdy porównamy ze sobą dwa ostatnie wzory, to możemy zauważyć, że napięcie
na zaciskach cewki wyprzedza w fazie przepływający przez nią prąd
o kąt fazowy
. Jeżeli za wektor podstawowy przyjąć wektor napięcia, to wektor prądu cewki opóźni się względem wektora napięcia o kąt
.

Równanie (4) wskazuje, że amplituda napięcia

(5)

zaś wartość skuteczna

(6)
.

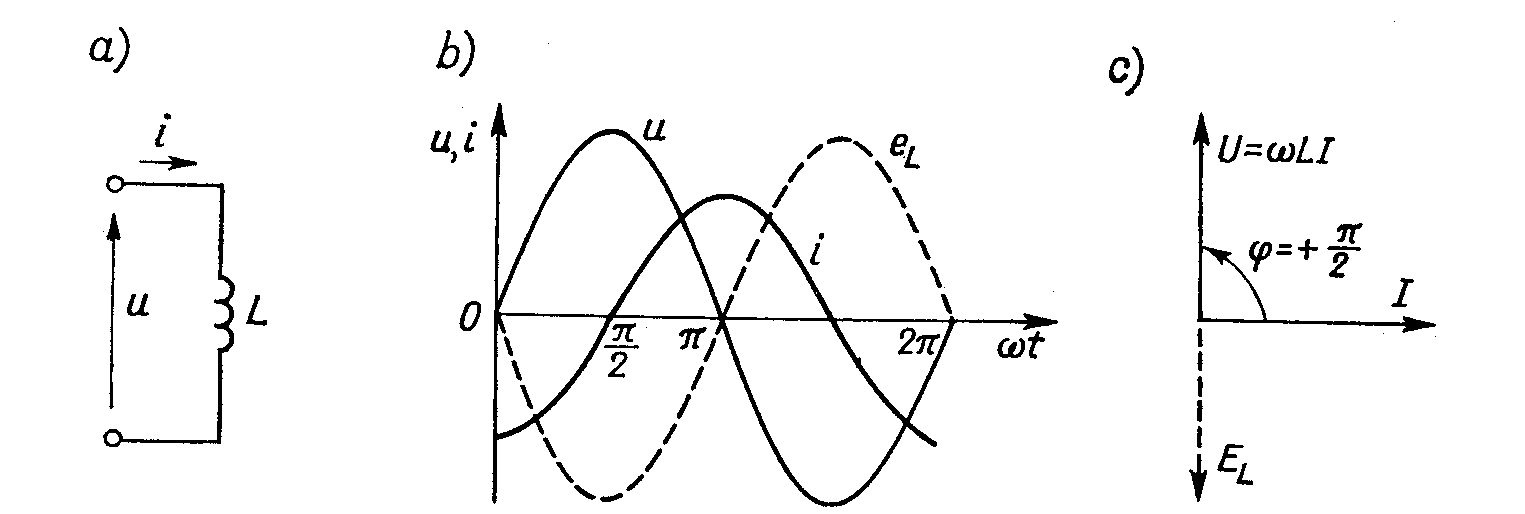
Rysunek 2

Powyższy rysunek przedstawia cewkę idealną w sieci prądu sinusoidalnego. Poszczególne podpunkty są to:

1. schemat połączeń

2. wykres czasowy napięcia i prądu

3. wykres wektorowy.

Równanie (6) ma postać podobną do prawa Ohma dla prądu stałego (
), dlatego przez analogię
nazwano oporem indukcyjnym lub reaktancją indukcyjną

(7)
.

Z równania (7) wynika ważna własność reaktancji indukcyjnej - proporcjonalność do częstotliwości
.

W obwodzie, w którym znajduje się idealna cewka, występuje przy przepływie prądu tylko indukcyjny spadek napięcia
, natomiast nie występuje strata mocy, ponieważ
, zaś moc jak wiadomo, wynosi
. Dlatego w obwodach prądu zmiennego rezystancja
nazywa się oporem czynnym, zaś reaktancja
- oporem biernym indukcyjnym. Iloczyn
nazywa się napięciem indukcyjnym.

Kondensator idealny.

Jeżeli do obwodu elektrycznego zostanie włączony kondensator (rysunek3), to jego dielektryk, będący izolatorem, działa jako przerwa w obwodzie. Mimo włączonego źródła napięcia prąd nie może przez niego przepływać. Bezpośrednio po przyłączeniu do źródła prądu stałego płynie jednak w przewodach doprowadzających czasowo ograniczony prąd ładowania
, który w czasie
doprowadza do okładzin kondensatora ładunek
. Jeżeli kondensator przyłączony będzie do źródła napięcia przemiennego, to jego elektrody będą na przemian ładowane i rozładowywane, wobec czego w przewodach popłynie prąd przemienny.

Wartość chwilowa prądu ładowania kondensatora wynosi:

(8)
.

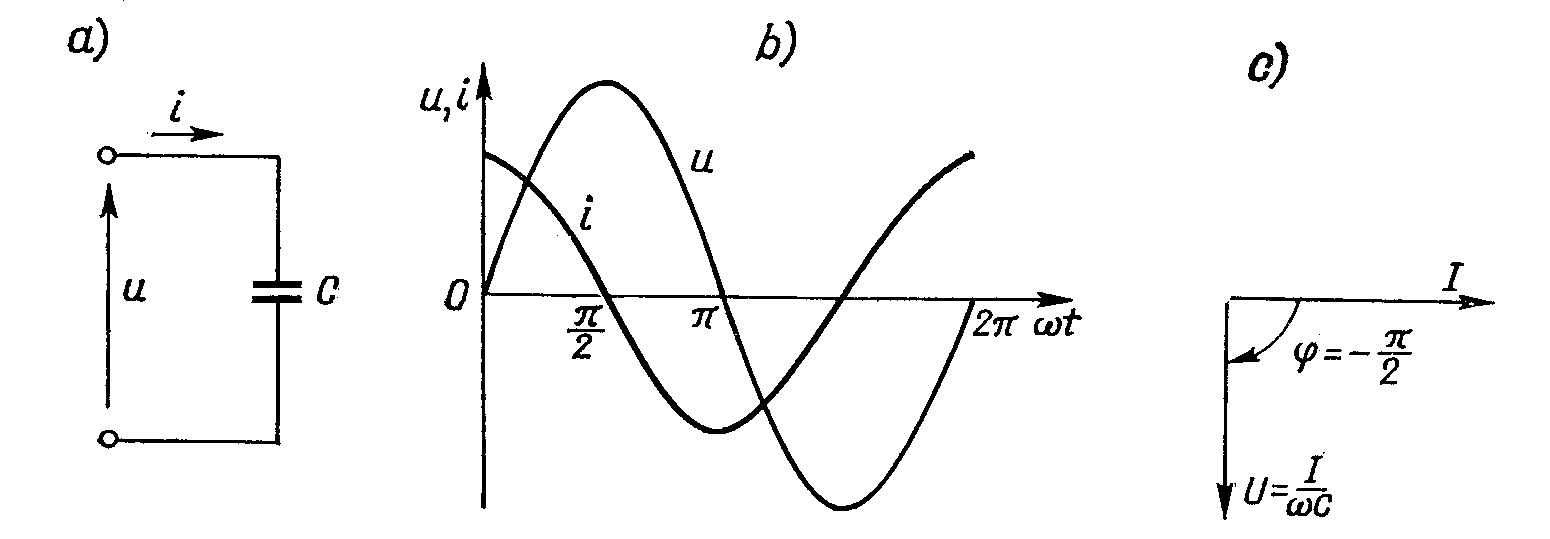
Rysunek 3

Powyższy rysunek przedstawia kondensator idealny w sieci prądu sinusoidalnego. Poszczególne podpunkty są to:

1. schemat połączeń

2. wykres czasowy napięcia i prądu

3. wykres wektorowy napięcia i prądu.

Ponieważ znany jest wzór
, więc przyrostowi ładunku
odpowiada przyrost napięcia
w czasie
, czyli

(9)
.

Z równań (8) i (9) otrzymamy:

.

Jeżeli kondensator włączony jest do napięcia:

(10)
,

to wartość chwilowa prądu ładowania wyniesie:

11. 
    

lub

(12)
.

Równania (11) i (12) wykazują, że prąd ładowania kondensatora wyprzedza napięcie o kąt fazowy
.

Z równania (12) wynika, że amplituda prądu ładowania wynosi:

(13)
,

zaś wartość skuteczna:

(14)
.

Równanie (13) ma postać prawa Ohma, więc wielkość
nazywa się oporem - biernym pojemnościowym lub reaktancją pojemnościową:

(15)
.

Jak widać z powyższego wzoru reaktancja pojemnościowa jest odwrotnie proporcjonalna do częstotliwości.

Iloczyn
nazywa się napięciem pojemnościowym. Równa się ono napięciu przyłożonemu do zacisków kondensatora.

2. Filtry RC.

Łącząc rezystory z kondensatorami wykonywać dzielniki napięcia zależne od częstotliwości, wykorzystując w tym celu zależność impedancji kondensatora
od częstotliwości. Układy tego typu mają taką własność, że przepuszczają sygnały o interesujących nas częstotliwościach, a tłumią sygnały o niepożądanych częstotliwościach.

Omówię tu kilka prostych przykładów filtrów RC.

Filtry górno przepustowe.

Filtr takiego typu jest przedstawiony na poniższym rysunku ( rysunek 4 ).

Rysunek 4

Dla takiego filtru otrzymamy następującą

zależność wykorzystując zespolone prawo Ohma:

(16)

Stąd napięcie na rezystorze
jest równe:

(17)
.

Najczęściej nie interesuje nas faza napięcia
a jedynie jego amplituda:

(18)
.

Sposób wyznaczania szeregowo połączonych impedancji R i C (rysunek 5) jest pokazany poniżej ( rysunek 6 ):

Rysunek 6

Rysunek 5

Odpowiedź tego układu, gdy pominiemy zależności

fazowe, rozważając jedynie moduły wielkości

zespolonych, wyraża się następująco:

(19)
Rysunek 7

,

i wygląda tak jak na rysunku obok

( rysunek 7 ).

Można zauważyć, że dla dużych

częstotliwości
napięcie wyjściowe jest w przybliżeniu równe napięciu wejściowemu i maleje do zera wraz ze zmniejszaniem się częstotliwości. Powszechnie jest używana nazwa „3 - decybelowa częstotliwość graniczna filtru” (lub jakiegokolwiek układu o charakterystyce filtru). W przypadku prostego filtru górnoprzepustowego RC częstotliwość graniczna jest dana wzorem:

(20)
.

Filtry dolnoprzepustowe.

Zamieniając miejscami R i C można otrzymać filtr o odwrotnym zachowaniu się w funkcji częstotliwości ( rysunek 8 ).

Wówczas:

(21)
.

Punkt zmniejszenia wzmocnienia o 3dB znowu odpowiada

częstotliwości:

Rysunek 8 (22)
.

Oto charakterystyka amplitudowa

filtru dolnoprzepustowego ( rysunek 9 ). Rysunek 9

Filtry pasmowe.

Filtr pasmowy powstaje z nałożenia elementów filtru dolnoprzepustowego o częstotliwości granicznej
i elementów filtru górnoprzepustowego o częstotliwości granicznej
, przy czym musi zachodzić warunek, że
. Filtr taki przepuszcza bez tłumienia częstotliwości w paśmie od
do
, poza tym pasmem tłumienie szybko rośnie.

Filtry zaporowe.

Filtr zaporowy powstaje poprzez nałożenie elementów filtru dolnoprzepustowego o częstotliwości granicznej
i elementów filtru dolnoprzepustowego o częstotliwości granicznej
przy czym musi zachodzić następujący warunek:
. Filtry te charakteryzują się tłumiennością w przybliżeniu wynoszącą zero gdy
oraz
. W paśmie tłumieniowym między częstotliwościami
i
tłumienność jest bardzo duża.

---