POLITECHNIKA GDAŃSKA Gdańsk, 21.03.2007
WYDZIAŁ INŻYNIERII LĄDOWEJ
I ŚRODOWISKA
KATEDRA MECHANIKI BUDOWLI I MOSTÓW
METODY DOŚWIADCZALNE W ANALIZIE KONSTRUKCJI

Ćwiczenie nr 13
Temat:
Wyznaczenie środka zginania.
Przygotowali:
Emilia Czech
Weronika Kitowska
Marek Cichocki
1. KRÓTKI OPIS POSZCZEGÓLNYCH DOŚWIADCZEŃ
Celem doświadczenia jest wyznaczenie środka zginania (lub ścinania) dwóch cienkościennych belek wspornikowych. Doświadczenie 1 przeprowadzono na belce o przekroju rurkowym, doświadczenie 2 na belce o przekroju kątowym.
Doświadczenia wykonujemy przy pomocy przyrządów pomiarowych odpowiednio ustawionych dla poszczególnych przekrojów.
Doświadczenie 1
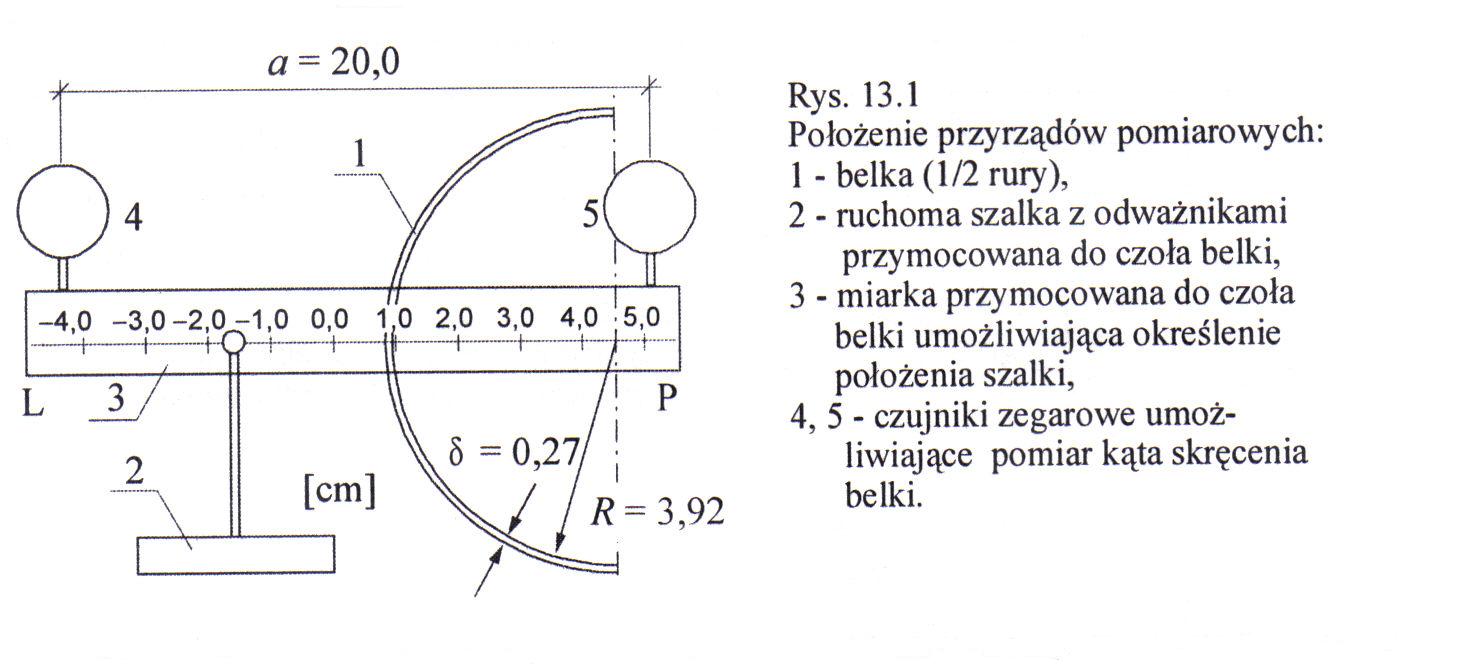
Doświadczenie 2
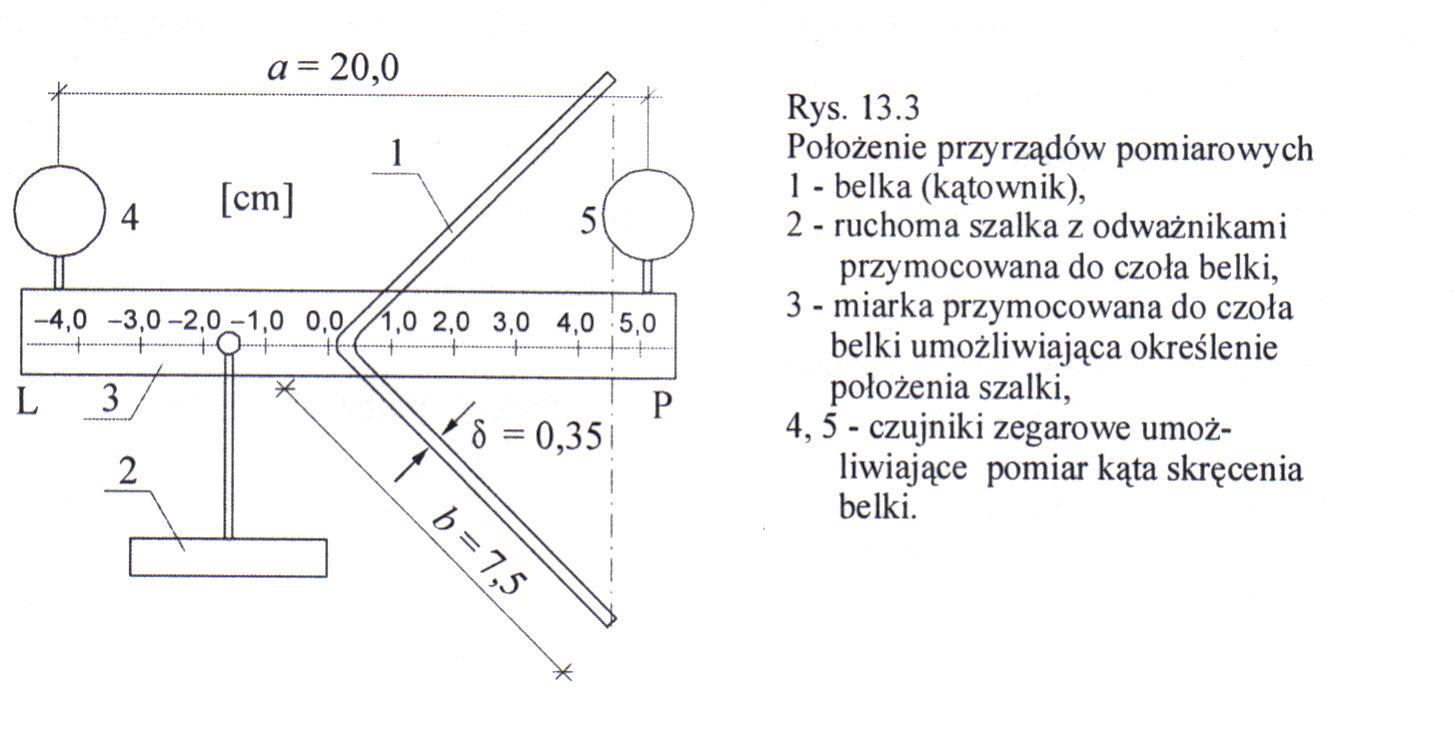
Przy pomocy odważników wywołujemy moment skręcający a na podstawie czujników dalej możemy wyznaczyć kąty przekrojów belek .
Doświadczenia rozpoczynamy i kończymy od pomiaru przemieszczeń na obu czujnikach przy nie obciążonym układzie w punkcie zerowym. Przy wyznaczeniu kąta obrotu uśredniamy odczyty początkowe z czujników w celu wyeliminowania błędu .Następnie obciążamy układ przez obciążenie szalki odważnikami i dokonujemy pomiarów przemieszczeń w granicach od -40mm do 40mm notując wskazania czujników zegarowych fl i fp co 10 mm. Następnie wykonujemy wykres funkcji ugięć w zależności od obciążenia . Punkt w którym proste z poszczególnych czujników się przecinają jest szukanym środkiem zginania .
2. WYNIKI POMIARÓW
Belka o przekroju rurowym
- Odczyty początkowe przy nieobciążonym układzie: fl1 = 3,00 , fp1 = 4,71
- Odczyty końcowe przy nieobciążonym układzie: fl2 = 3,00 , fp2 = 4,70
- Średnie odczyty początkowe: fl0 = 0,5( fl1 + fl2 ) = 0,5 (3,00+3,00) = 3,00
fp0 = 0,5( fp1 + fp2) = 0,5 (4,71+4,70) = 4,705
- Kąt skręcenia ze wzoru : Ф=(ul-up)/a
gdzie : ul=fl - fl0
up=fp - fp0
a=200 mm
Położenie siły [mm] |
Wskazania czujników |
Ugięcia punktów |
Kąt skręcenia Φ [rad] |
||
|
Lewego fl |
Prawego fP |
Lewego ul |
Prawego up |
|
-40 |
2,02 |
5,31 |
-0,98 |
0,605 |
-0,007925 |
-30 |
2,28 |
5,04 |
-0,72 |
0,335 |
-0,005275 |
-20 |
2,45 |
4,87 |
-0,55 |
0,165 |
-0,003575 |
-10 |
2,65 |
4,67 |
-0,35 |
-0,035 |
-0,001575 |
0 |
2,97 |
4,61 |
-0,03 |
-0,095 |
+0,000325 |
10 |
3,07 |
4,25 |
+0,07 |
-0,455 |
+0,002625 |
20 |
3,28 |
4,05 |
+0,28 |
-0,655 |
+0,004675 |
30 |
3,54 |
3,81 |
+0,54 |
-0,895 |
+0,007175 |
40 |
3,70 |
3,645 |
+0,70 |
-1,06 |
+0,0088 |
Wykres:
Belka o przekroju kątowym
- Odczyty początkowe przy nieobciążonym układzie: fl1 = 2,10 , fp1 = 3,85
- Odczyty końcowe przy nieobciążonym układzie: fl2 = 2,08 , fp2 = 3,87
- Średnie odczyty początkowe: fl0 = 0,5( fl1 + fl2 ) = 0,5 (2,10+2,08) = 2,09
fp0 = 0,5( fp1 + fp2) = 0,5 (3,85+3,87) = 3,86
- Kąt skręcenia ze wzoru : Ф=(ul-up)/a
gdzie : ul=fl - fl0
up=fp - fp0
a=200 mm
Położenie siły [mm] |
Wskazania czujników |
Ugięcia punktów |
Kąt skręcenia Φ [rad] |
||
|
Lewego fL |
Prawego fP |
Lewego uL |
Prawego uP |
|
-40 |
1,49 |
4,37 |
-0,6 |
0,51 |
-0,00555 |
-30 |
1,62 |
4,24 |
-0,47 |
0,38 |
-0,00425 |
-20 |
1,75 |
4,01 |
-0,34 |
0,15 |
-0,00245 |
-10 |
1,88 |
3,95 |
-0,21 |
0,09 |
-0,0015 |
0 |
2,09 |
3,84 |
0 |
-0,02 |
+0,0001 |
10 |
2,14 |
3,68 |
0,05 |
-0,18 |
+0,00115 |
20 |
2,29 |
3,52 |
0,2 |
-0,34 |
+0,0027 |
30 |
2,39 |
3,42 |
0,3 |
-0,44 |
+0,0037 |
40 |
2,51 |
3,30 |
0,42 |
-0,56 |
+0,0049 |
Wykres:
3. TEORETYCZNE OBLICZENIA
3.1. Przekrój pierścieniowy zamknięty
R=3,92 cm
dA=dSδ dS=Rdϕ
dA=Rδdϕ
y=Rcosϕ
Środek zginania - punkt w którym należy przyłożyć siłę aby zredukować wypadkową naprężeń stycznych ( siła w tym punkcie nie wywołuje skręcania ) .
czyli:
∑ Ms0=0 , stąd :
T x - ∫ dt R = 0
T x - t R = 0 (1) t- wypadkowa naprężeń stycznych
τ = (Sx T)/(Ix δ) Ix-moment bezwładności przekroju:
Ix = 0,5 Π R3δ
Sx-moment statyczny:
Sx = ∫ y dA
Sx = ∫ R cosϕ R δ dϕ = ∫ R2 δ cosϕ dϕ = R2 δ cosϕ + c
Wiedząc , że dla: Sx (ϕ = 0) = 0 , stała c = 0 .
Sx = R2 δ sinϕ .
τ = (R2 δ sinϕ T)/( 0,5 Π R3δ δ) = ( 2 sinϕ T)/(R δ Π )
t = ∫ τ dA = ∫ (( 2 sinϕ T )/( R δ Π )) R δ dϕ = ( 2 T ) / Π [ - cosϕ ] = ( 2 T ) / Π [ - ( -1-1)] = 4 T / Π .
Podstawiając do równania (1) , otrzymujemy :
T x = (4 T / Π) R
x = ( 4/Π ) R = 4 (3,92/Π) = 4,99 cm
Zgodnie z przyjętym układem współrzędnych w doświadczeniu odległość od punktu zginania równa się :
e = 4,50 - 4,99 = - 0,49 cm .
3.2. Przekrój pierścieniowy otwarty
Korzystam z warunku jak w 3.1:
∑ Ms0=0 , stąd :
Ty x - T1 a - T2 a = 0
∑X = 0 , stąd :
T1 = T2
∑Y = 0 , stąd :
Ty = T1 + T2
podstawiając do równania (1)
(T1 + T2 ) x = (T1 + T2 ) a
x = a
Wiedząc , że a = 5,3 cm otrzymujemy : x = 5,3 cm .
Zgodnie z przyjętym układem współrzędnych w doświadczeniu, odległość od punktu zginania równa się
e = 5,50 - 5,30 = 0,20 cm.
4. Porównanie wyników doświadczeń z obliczeniami teoretycznymi
RODZJ PRZEKROJU |
WARTOŚĆ DOŚWIADCZALNA |
WARTOŚĆ TEORETYCZNA |
RUROWY |
|
-4,9 |
KĄTOWY |
|
2,0 |
5. Obliczenie położenia środka ciężkości przekroju poprzecznego belki
Przekrój rurowy
δ , cm
R=3,92 cm
xc = Sy/A
A = ∫Rδdφ= Rπδ
Sx = 0 - przekrój monosymetryczny, w związku z tym yc = 0
x x
Sy = ∫xdA = - δR2∫sinφdφ = δR2cosφ│ = -2δR2
A 0 0
A = 3,92·0,27·π = 3,325 cm2
Sy = -2·0,27·(3,92)2 = -8,298 cm3
xc = -8,298 / 3,325 = - 2,495 cm
C(xC;yC)=C(-2,495 ; 0)
Przekrój kątowy
δ = 0,35 cm
xC=
cm
C(xC;yC)=C(-2,65 ; 0)
6. Pomiar kąta skręcania dla przypadku obciążenia siłą przyłożoną w środku ciężkości
6.1. Przekrój rurowy
4,5 cm - 2,495 cm 2,0 cm - środek ciężkości znajduje się mniej więcej w
miejscu +20 mm na skali, dlatego też do obliczeń kąta skręcania bierzemy odczyty dla
położenia siły +20 mm
ul =0,28
up =-0,655
ϕ = ( ul - up )/a = 0.004675 rad
6.2. Przekrój kątowy
5,5 cm - 2,65 cm = 2,85 cm -środek ciężkości znajduje się pomiędzy
wartością +20 i +30 mm na skali , dlatego też wartości uL i uP wyznaczamy poprzez interpolację liniową
ul =0,25
up =-0,39
ϕ = ( ul - up )/a = 0.0032 rad
7. Uwagi własne
W wykonywanym ćwiczeniu zarówno w doświadczeniu nr1 jak i w doświadczeniu nr2 , wyznaczaliśmy środki zginania, czyli punkty w których należy przyłożyć siłę tnącą aby nie wywołała momentu skręcającego .Studiując wykresy funkcji ugięć w zależności od obciążenia znajdujemy punkt przecięcia się dwóch wykresów - jest to punkt w którym nie występuje skręcenie czyli nasz szukany punkt .
Położenie punktu wyznaczone doświadczalnie i teoretycznie różni się nieznacznie zarówno przy przekroju rurowym jak i kątowym . Różnicę tę upatrujemy:
- w niedokładności pomiarów - wiąże się to z niedokładnością przyrządów oraz błędnego
odczytania z czujników pomiarowych .
- niedokładnego naniesienia punktowo wykresu potrzebnego do określenia środka zginania
- niedokładnego odczytu położenia środka zginania z w.w. wykresu.
7
Wyszukiwarka
Podobne podstrony:
6 Środek masy
9 Zginanie uko Ťne zbrojenie min beton skr¦Öpowany
obliczanie zginanych el sprezonych
cw7 (zginanie)
zginanie proste
Zginanie prętów obciążenie ciągłe
Środek masy, Biomechanika i Robotyka
06 Próba statyczna zginania
Statyczna próba zginania materiału Ćwiczenie 5
srodek
9 zajęcia mechanika środek ciężkości=
Algorytm wymiarowania zbrojenia według metody ogólnej w zginanym elemencie teowym
srodek cięzkości trójkąta
3 ?danie wytrzymałości na zginanie oraz udarności 1
algorytm przekroju zginanego prostokątnego
2 Projektowanie przekroju zginanego
zginanie poprzeczne
Zginanie zadania
zginanie 2, 3 semestr, Wytrzymka laborki
więcej podobnych podstron