LABOLATORIUM z Wytrzymałości Materiałów	Tadeusz Glica
		Grupa: 32	Data: 20.12.2000
Temat: Wyznaczanie Eulerowskiej Sily Krytycznej Belki .	Nr ćwiczenia: 5	Ocena:

TEORIA

Załóżmy przypadek belki doskonale prostej, do której przykładamy siłę P dokładnie wzdłuż osi. Niech siła P rośnie powoli od 0. Przy niedużych wartościach P, po wychyleniu belki z pozycji prostej za pomocą niewielkiego bocznego obciążenia zakłócającego, a następnie odjęciu tej siły, belka wróci do prostej postaci (równowaga stateczna, trwała). Przy pewnej krytycznej wartości P (obciążenie krytyczne) belka nie powróci do postaci prostej, pozostanie wygięta, będzie mogła przyjmować każde z położeń określonych strzałką wychylenia (równowaga obojętna).

Wykonanie idealnie prostej belki z idealnie przyłożoną siłą P nie jest możliwe w rzeczywistości. Dla eksperymentalnego wyznaczenia P_kr posłużyliśmy się metodą Southwella.

Rozważmy przypadek belki z imperfekcją - oś tej belki jest wstępnie odkształcona, a wstępna linia ugięcia w₀(x) ma taki przebieg, jaki posiadałaby belka idealnie prosta - wychylona z położenia w(x)=0 w chwili osiągnięcia eulerowskiego obciążenia krytycznego ( w₀ (x) = w₀ (l) [1 - cos(πx/(2l))] ) .

Linia ugięcia w(x) dla tej belki: M(x)=P{w(l)+wo(l)-[w(x)+w0(x)]}; w''(x)=M(x)/(EJ)

Mierząc ugięcie w(P, x) w pewnym punkcie belki x₀ przy znanej sile P możemy obliczyć krytyczną siłę.

Dla x = x₀ mamy:

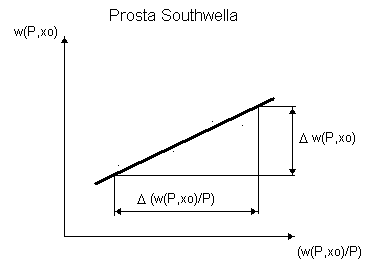
Przy wielokrotnym wykorzystaniu tego samego modelu belki trudno jest zachować tę samą, pierwotnie nadaną postać wstępnej linii ugięcia. W modelu wykorzystanym w ćwiczeniu wykorzystano inny rodzaj im perfekcji- siłę P przyłożono w mimośrodzie e. Jest to przybliżona metoda wyznaczenia P_kr (M(x)=P[e+w(l)-w(x)]).

Rozwiązując równanie w''+k²w=k²[e+w(l)] (k²=P/(EJ)) w sposób przybliżony - wychodząc od sformułowania wariacyjnego, dla którego równaniem Eulera jest powyższe równanie różniczkowe- otrzymujemy funkcję ugięcia w postaci:

PRZEKSZTAŁCENIE WZORU.

PRZEBIEG I WYNIKI

Działamy na pręt siłą przyłożoną na mimośrodzie. W kolejnych trzech pomiarach zmieniamy wartość mimośrodu i tak kolejno e=8, e=16, e=24. Na obciążniku zawieszamy kolejno szalki, które stanowią zwiększenie obciążenia. Odczytujemy z obu wskaźników wartości odchylenia pręta. Następnie porównujemy je z wartością zerowaną i obliczamy wartość średnią, która jest równa W.

Lp.	Mimośród e [mm]	Wskazania czujników						W mm^3			W/P mm^3/N
				P1=10[N]		P2=20[N]								P3=30[N]
				L	R	L	R	L	R	P1	P2	P3	P1	P2	P3
1	8	+4	-4	+30	-30	+60	-60	0.526	1.278	2.439	0.0526	0.1278	0.2439
2	16	+40	-40	+130	-130	+294	-298	1.052	2.556	4.879	0.1052	0.2556	0.4879
3	24	+85	-87	+248	-251	+520	-526	1.579	3.834	7.319	0.1579	0.3843	0.7319

dł. belki l = 1000 [mm]

wymiary poprzeczne b x h = 13 x 5 [mm]

przemieszczenia mierzone w punkcie x₀ = l/2

PORÓWNANIE SIŁY KRYTYCZNEJ Z WYKRESU Z SIŁĄ TEORETYCZNĄ.

Pkr (obliczeniowa) = 66,74 N

Pkr (z wykresu) = 45.5 N; 39.6N; 28.91 N

WNIOSKI.

Ćwiczenie polegało na wyznaczeniu siły krytycznej ,to znaczy takiej przy której belka znajdzie się w stanie równowagi obojętnej(robiliśmy to dla belki o przekroju 13 na 5 mmm i o długości 1000mm). Wychylenie belki dokonywaliśmy za pomocą przykładania coraz to większej siły i poprzez przykładanie siły w mimośrodzie (dla e =8mm, e = 16mm, e =24mm). Z przeprowadzonych badań wynika, że siła krytyczna obliczeniowa nie jest równa co do wartości sile krytycznej odczytanej z wykresów .Różniące się wartości siły krytycznej odczytane z wykresów z wyliczoną teoretycznie wskazują ze znajdowaliśmy się w stanie równowagi statecznej (co można było zaobserwować podczas wykonywania ćwiczenia ponieważ belka powracała w pierwotne położenie). Wyznaczenie siły krytycznej dla belek (prętów)jest ważne ponieważ w pobliżu tej siły belka bardzo szybko zmienia swoje położenie i przyjmuje po przekroczeniu wartości siły krytycznej położenie obojętne(to znaczy zajmuje położenie inne niż stateczne).W konstrukcjach inżynierskich wykorzystuje się wiele belek (prętów) dlatego też dokładne wyznaczenie siły krytycznej jest bardzo ważne, ponieważ wiemy w jakim zakresie taki pręt będzie spełniał swe zadanie

2

---