LABOLATORIUM z Wytrzymałości Materiałów	Tadeusz Glica
		Grupa: 32	Data: 26.12.2000
Temat: Wyznaczanie Eulerowskiej Sily Krytycznej Belki .	Nr ćwiczenia: 5	Ocena:

TEORIA

Załóżmy przypadek belki doskonale prostej, do której przykładamy siłę P dokładnie wzdłuż osi. Niech siła P rośnie powoli od 0. Przy niedużych wartościach P, po wychyleniu belki z pozycji prostej za pomocą niewielkiego bocznego obciążenia zakłócającego, a następnie odjęciu tej siły, belka wróci do prostej postaci (równowaga stateczna, trwała). Przy pewnej krytycznej wartości P (obciążenie krytyczne) belka nie powróci do postaci prostej, pozostanie wygięta, będzie mogła przyjmować każde z położeń określonych strzałką wychylenia (równowaga obojętna).

Wykonanie idealnie prostej belki z idealnie przyłożoną siłą P nie jest możliwe w rzeczywistości. Dla eksperymentalnego wyznaczenia P_kr posłużyliśmy się metodą Southwella.

Rozważmy przypadek belki z imperfekcją - oś tej belki jest wstępnie odkształcona, a wstępna linia ugięcia w₀(x) ma taki przebieg, jaki posiadałaby belka idealnie prosta - wychylona z położenia w(x)=0 w chwili osiągnięcia eulerowskiego obciążenia krytycznego ( w₀ (x) = w₀ (l) [1 - cos(πx/(2l))] ) .

Linia ugięcia w(x) dla tej belki: M(x)=P{w(l)+wo(l)-[w(x)+w0(x)]}; w''(x)=M(x)/(EJ)

Mierząc ugięcie w(P, x) w pewnym punkcie belki x₀ przy znanej sile P możemy obliczyć krytyczną siłę.

Dla x = x₀ mamy:

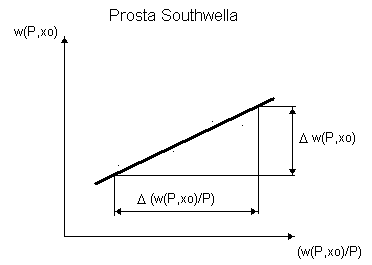
Przy wielokrotnym wykorzystaniu tego samego modelu belki trudno jest zachować tę samą, pierwotnie nadaną postać wstępnej linii ugięcia. W modelu wykorzystanym w ćwiczeniu wykorzystano inny rodzaj im perfekcji- siłę P przyłożono w mimośrodzie e. Jest to przybliżona metoda wyznaczenia P_kr (M(x)=P[e+w(l)-w(x)]).

Rozwiązując równanie w''+k²w=k²[e+w(l)] (k²=P/(EJ)) w sposób przybliżony - wychodząc od sformułowania wariacyjnego, dla którego równaniem Eulera jest powyższe równanie różniczkowe- otrzymujemy funkcję ugięcia w postaci:

PRZEKSZTAŁCENIE WZORU.

PRZEBIEG I WYNIKI

Działamy na pręt siłą przyłożoną na mimośrodzie. W kolejnych trzech pomiarach zmieniamy wartość mimośrodu i tak kolejno e=8, e=16, e=24. Na obciążniku zawieszamy kolejno szalki, które stanowią zwiększenie obciążenia. Odczytujemy z obu wskaźników wartości odchylenia pręta. Następnie porównujemy je z wartością zerowaną i obliczamy wartość średnią, która jest równa W.

Lp.	Mimośród e [mm]	Wskazania czujników						W mm^3			W/P mm^3/N
				P1=10[N]		P2=20[N]								P3=30[N]
				L	R	L	R	L	R	P1	P2	P3	P1	P2	P3
1	8	+4	-4	+30	-30	+60	-60	0.526	1.278	2.439	0.0526	0.1278	0.2439
2	16	+40	-40	+130	-130	+294	-298	1.052	2.556	4.879	0.1052	0.2556	0.4879
3	24	+85	-87	+248	-251	+520	-526	1.579	3.834	7.319	0.1579	0.3843	0.7319

dł. belki l = 1000 [mm]

wymiary poprzeczne b x h = 13 x 5 [mm]

przemieszczenia mierzone w punkcie x₀ = l/2

PORÓWNANIE SIŁY KRYTYCZNEJ Z WYKRESU Z SIŁĄ TEORETYCZNĄ.

Pkr (obliczeniowa) = 66,74 N

Pkr (z wykresu) = 45.5 N; 39.6N; 28.91 N

WNIOSKI.

Z przeprowadzonych badań wynika, że siła krytyczna obliczeniowa nie jest równa co do wartości sile krytycznej odczytanej z wykresu. Siły odczytane z wykresu dla trzech serii pomiarów także różnią się od siebie. Możemy wywnioskować ,że duże różnice między Pkr (obliczeniową) ,a Pkr (z wykresu) są spowodowane błędnymi odczytami z czujników.

2

---