Laboratorium Fizyki III

SPRAWOZDANIE

Ćw.1 :

Temat: Badanie charakterystyki licznika Geigera-Mullera i statystycznego charakteru rozpadu promieniotwórczego

Piotr Soszyński grMU-71 zespół 6

Cel ćwiczenia:

Przeprowadzone ćwiczenie miało na celu wyznaczenie charakterystyki licznika Geigera - Mullera oraz wyznaczenie jego czasu martwego.

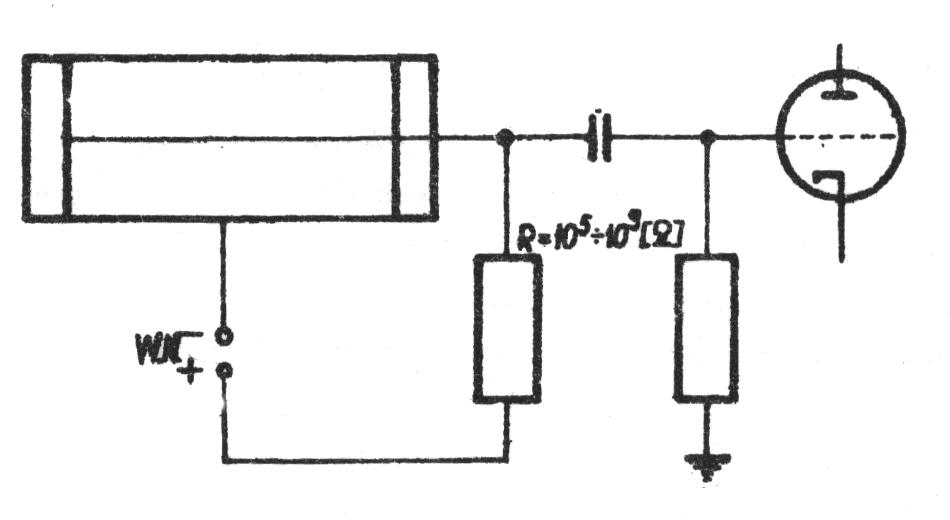
Opis układu pomiarowego i zasada jego działania:

Licznik Geigera-Mullera jest detektorem używanym do wykrywania promieniowania wysyłanego przez izotopy radioaktywne. Zbudowany jest z dwóch elektrod : cylindrycznej katody i umie­szczonej wzdłuż jej osi odizolowanej nici - anody. Całość jest szczelnie zamknięta i wypełniona gazem pod zmniejszonym ciśnieniem. Do elektrod doprowadza się wysokie napięcie, przy czym nić - anoda otrzymuje potencjał dodatni. Poniższy rysunek (rys.1) przedstawia budowę licznika G - M na promieniowanie β kielichowego lub sztorcowego (rys.1c) oraz licznika na promie­niowanie γ cylindrycznego (rys. 1a, 1b). Rysunek 2 pokazuje spo­sób włączenia licznika do aparatury pomiarowej. Liczniki okien­kowe na promieniowanie γ zbudo­wane są podobnie jak liczniki na promieniowanie β nie po­siadają jednak okienka mikowego względnie okienko to ma wię­kszą grubość. Mimo to liczniki na promieniowanie beta rejestrują promieniowanie gamma, jednak nie stosuje się ich do jego wykrywania ze względu na małą wydajność. Wynika to z faktu, że działanie licznika na promieniowanie gamma spowodowane jest powstawaniem wtórnych elektronów ( promieniowanie gamma nie jonizuje bezpośrednio ośrodka, przez które przechodzi w przeciwieństwie do beta). Należy zatem grubość ścianki dobrać tak, aby powstawało ich możliwie dużo.

Działanie licznika G - M. jest następujące:

Gdy przez komorę licznika przejdzie cząstka naładowana lub kwant gamma, gaz zawarty w liczniku zostaje zjonizowany ( bezpośrednio lub przez elektrony wtórne). Tak powstałe elektrony i jony poruszają się pod wpływem przyłożonego pola elektrycznego ku katodzie i anodzie. Gdy zostaną przyśpieszone (przez pole) do odpowiednio

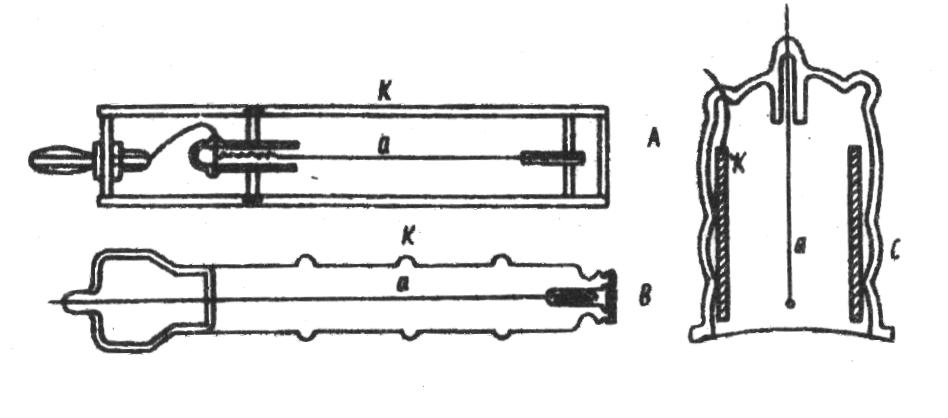
Rys. 1 Przykłady liczników Geigera - Mullera.

Rys. 2 Sposób podłączenia licznika Geigera - Mullera.

dużych energii to mogą wzbudzać lub jonizować dalsze atomy gazu. Procesom tym towarzyszy emisja promieniowania ultrafioletowego, które poprzez proces fotojonizacji przyśpieszają proces rozprzestrzeniania się wyładowania elektrycznego na całą komorę. Na oporze R załączonym szeregowo do obwodu zasilania licznika powstaje impuls napięcia, który jest sygnałem na wyjściu. Aby licznik mógł zarejestrować przejście kolejnej cząstki lub też kwantu gamma wyładowanie lawinowe musi zostać zatrzymane w jak najkrótszym czasie. Osiąga się to, poprzez zastosowanie odpowiedniej aparatury elektronicznej lub przez wypełnienie komory licznika odpowiednią mieszaniną gazów (np. argon z dodatkiem ok. 10% par alkocholu).

Licznik G - M. nie daje możliwości rozróżnienia poszczególnych cząstek, uwarunkowane jest to, zakresem napięć, w którym licznik pracuje. W tym obszarze wszystkie impulsy mają tą samą wartość niezależnie od zdolności jonizacyjnej cząstek.

POMIAR MOCY DAWKI

Pierwszym etapem ćwiczenia był pomiar mocy dawki pochłoniętej za pomocą radiometru. Urządzenie to pozwala na badanie mocy dawki pochłoniętej od dwóch stron: cienkościennej i grubościennej.

Otrzymaliśmy następujące wyniki:

-od strony grubościennej licznik wskazał 4 μGy/h

-od strony cienkościennej licznik wskazał 60cz μGy/h

Wyniki pomiarów świadczą o tym, że promieniowanie jest bardzo mało przenikliwe. Strona grubościenna detektora powstrzymała niemal całe promieniowanie próbki. Możemy zatem wnioskować, że mamy do czynienia z promieniowaniem β.

Przystąpiliśmy do zdejmowania charakterystyki roboczej badanego licznika. W tym celu napięcie ustawiliśmy na 720V a czas liczenia na 60 sekund, po dokonaniu pomiaru liczby zliczeń w zadanym czasie zmniejszaliśmy napięcie o 10V i powtarzaliśmy pomiar, aż do osiągnięcia napięcia progowego. Wyniki przedstawia tabela 2.

U [V]	N [imp]	I [ imp/ min]	σ = √I/t
462	655	3930	8,09
464	799	4794	8,94
466	1031	6186	10,15
468	1407	8442	11,86
470	1617	9702	12,72
480	2015	12090	14,20
490	2025	12150	14,23
500	2071	12426	14,39
510	2093	12558	14,47
520	2076	12456	14,41
530	2170	13020	14,73
540	2141	12846	14,63
550	2180	13080	14,76
560	2260	13560	15,03
570	2245	13470	14,98
580	2338	14028	15,29
590	2479	14874	15,74
600	2462	14772	15,69
610	2599	15594	16,12
620	2729	16374	16,52
630	2745	16470	16,57
640	3018	18108	17,37
650	3326	19956	18,24
660	3641	21846	19,08
670	4151	24906	20,37
680	5137	30822	22,66
690	6170	37020	24,84
700	7408	44448	27,22
710	8380	50280	28,95
720	9273	55638	30,45

Tabela 2

Dysponując powyższym wykresem przystąpiłem do wyznaczenia:

1. napięcia pracy licznika:

stąd :

2. długości plateau:

V₂ - V₁ = 640 -475 = 165 [V]

Na podstawie zebranych dotąd danych sporządziłem metryczkę licznika (tab. 3)

Napięcie progowe [V]	≈ 460
Napięcie pracy [V]	557,5
Długość plateau [V]	165

Tabela 3 Metryczka licznika.

Kolejny etap ćwiczenia polegał na wyznaczeniu czasu martwego licznika G - M. W tym celu pod licznikiem umieściliśmy preparat i dokonaliśmy pomiaru w ciągu 180 sekund. Następnie nie ruszając pierwszego preparatu umieściliśmy pod licznikiem drugi i ponownie zmierzyliśmy szybkość liczenia w ciągu 180 sekund. Potem usunęliśmy z komory licznika preparat pierwszy i przeprowadziliśmy pomiary aktywności preparatu drugiego. Na końcu z komory usunęliśmy wszystkie próbki i rozpoczęliśmy pomiar liczby zliczeń także w czasie 180 sekund (zdjęliśmy tzw. „tło licznika”). Otrzymane wartości zawiera tabela 4.

Tabela 4.

CZAS MARTWY LICZNIKA

Nr. preparatu	t [min]	N [imp]	IN [imp/min]	I = IN - Itła
1	3,5	33616	9604,6	9588,6
1+2	3,5	76030	21722,9	21706,9
2	3,5	46826	13378,9	13362,9
Bez preparatu	3,5	56	16	-

Korzystając ze wzoru oraz uwzględniając tło:

Kolejnym etapem tego ćwiczenia był pomiar aktywności próbki za pomocą okienkowego licznika G - M. Wyniki, które otrzymałem zawiera tabela 5. Dokładna ich analiza wskazuje na to, iż badany preparat wysyłał promieniowanie beta, gdyż promieniowanie to jonizuje bezpośrednio ośrodek i nie potrzebuje materii (która de facto osłabia je) w oddziaływaniu z którą powstałyby elektrony wtórne powodujące jonizację gazu w komorze licznika. Reasumując gdyby próbka wysyłała kwanty gamma to pomiar wykazałby większą jej aktywność po stronie bez okienek (czyli odwrotnie niż u nas).

Tabela 5.

BADANIE STATYSTYCZNE CHARAKTERU PRZEMIANY PROMIENIOTWÓRCZEJ
Rozkład doświadczalny					Rozkład Poissona		Rozkład Gaussa
A	B	C	D	E	F	G	H	I	J	K
k	n(k)	P(k)	k*P(k)	k^2*P(k)	Pp(k)	np(k)	x	rG	PG	nG(k)
6	4	0,0026	0,02	0,09	0,0026	4	-2,62	0,0128	0,0034	5
7	7	0,0045	0,03	0,22	0,0060	9	-2,36	0,0247	0,0065	10
8	20	0,0129	0,10	0,83	0,0120	19	-2,10	0,0443	0,0116	18
9	21	0,0135	0,12	1,10	0,0214	33	-1,83	0,0741	0,0195	30
10	54	0,0348	0,35	3,48	0,0342	53	-1,57	0,1159	0,0304	47
11	67	0,0432	0,48	5,23	0,0498	77	-1,31	0,1692	0,0444	69
12	104	0,0671	0,81	9,66	0,0663	103	-1,05	0,2306	0,0605	94
13	131	0,0845	1,10	14,28	0,0815	126	-0,78	0,2932	0,0770	119
14	156	0,1006	1,41	19,73	0,0931	144	-0,52	0,3481	0,0914	142
15	157	0,1013	1,52	22,79	0,0993	154	-0,26	0,3857	0,1012	157
16	168	0,1084	1,73	27,75	0,0992	154	0,00	0,3989	0,1047	162
17	146	0,0942	1,60	27,22	0,0933	145	0,27	0,3852	0,1011	157
18	122	0,0787	1,42	25,50	0,0829	128	0,53	0,3471	0,0911	141
19	120	0,0774	1,47	27,95	0,0698	108	0,79	0,2920	0,0766	119
20	90	0,0581	1,16	23,23	0,0558	86	1,05	0,2293	0,0602	93
21	61	0,0394	0,83	17,36	0,0425	66	1,32	0,1680	0,0441	68
22	49	0,0316	0,70	15,30	0,0309	48	1,58	0,1150	0,0302	47
23	29	0,0187	0,43	9,90	0,0215	33	1,84	0,0734	0,0193	30
24	16	0,0103	0,25	5,95	0,0143	22	2,10	0,0438	0,0115	18
25	11	0,0071	0,18	4,44	0,0091	14	2,36	0,0243	0,0064	10
26	7	0,0045	0,12	3,05	0,0056	9	2,63	0,0126	0,0033	5
27	4	0,0026	0,07	1,88	0,0033	5	2,89	0,0061	0,0016	2
28	2	0,0013	0,04	1,01	0,0019	3	3,15	0,0028	0,0007	1
29	2	0,0013	0,04	1,09	0,0010	2	3,41	0,0012	0,0003	0
30	2	0,0013	0,04	1,16	0,0006	1	3,68	0,0005	0,0001	0
	Suma:		Suma:	Suma:
	1550		15,99	270,19	3,81

Liczebność serii pomiarowej n=n(k)= 1550

Wartość oczekiwana 15,99

Odchylenie standardowe 3,81

HISTOGRAMY

Wnioski:

W ćwiczeniu tym zapoznałem się z przyrządami służącymi do wykrywania promieniowania wysyłanego przez izotopy radioaktywne. Za pomocą radiometru badaliśmy moc dawki pochłoniętej, ścianką cienkościenną i grubościenną urządzenia. Na podstawie pomiarów przeprowadzonych radiometrem wywnioskowaliśmy, że promieniowanie emitowane przez próbkę jest bardzo słabo przenikliwe i najprawdopodobniej mamy do czynienia z promieniowaniem β. W dalszej części ćwiczenia zajęliśmy się badaniem charakterystyk roboczej licznika. Jest to krzywa w układzie napiecie-szybkość zliczania impulsów imp/min. Z wykresu możemy odczytać napięcie progowe, czyli takie napięcie, poniżej którego impulsy na wyjściu są tak małe, że nie są rejestrowane przez układ liczący. Na wykresie możemy też zauważyć odcinek charakterystyki od V1 do V2 jest to tzw. `plateau' licznika, czyli obszar charakterystyki, w którym ilość zliczanych impulsów nie zależy od napięcia. Jest to najlepszy obszar pracy licznika, ponieważ tym zakresie rejestruje on 99% dostających się do niego cząstek naładowanych. Po wyżej napięcia V2 szybkość zliczanych impulsów wzrasta, co tłumaczy się wzrostem prawdopodobieństwa wyładowania samorzutnego. Następną częścią ćwiczenia było określenie czasu martwego licznika. Jest to czas potrzebny na wygaszenie wyładowania lawinowego i jest to czas, w którym licznik nie jest zdolny do zarejestrowania kolejnej cząstki jonizującej. W dalszej części ćwiczenia zajęliśmy badaniem statystycznego charakteru rozpadu promieniotwórczego. Możemy zauważyć z wykresu, że proces ten ma charakter przypadkowy i ze możemy opisać go za pomocą funkcji prawdopodobieństwa. Dla danego przypadku n=1550 obie funkcje w miarę dokładny sposób aproksymują dany rozrzut.

1

---