Opis teoretyczny

Wewnętrznym zjawiskiem fotoelektrycznym nazywamy zmianę rozkładu energetycznego elektronów w stałych i ciekłych półprzewodnikach i dielektrykach spowodowaną oddziaływaniem światła z daną substancją. Przejawia się ono w zmianie koncentracji nośników prądu w ośrodku i prowadzi do pojawienia się fotoprzewodnictwa lub zjawiska fotoelektrycznego w warstwie zaporowej. Fotoprzewodnictwem nazywamy zwiększenie przewodnictwa elektrycznego substancji (zmniejszenie jej oporności) w wyniku oddziaływania ze światłem. Działające na tej zasadzie przyrządy nazywamy fotooporami. Zjawiskiem fotoelektrycznym w warstwie zaporowej nazywamy powstawanie w wyniku oddziaływania ze światłem siły elektromotorycznej SEM (foto-SEM) w układzie składającym się z będących w kontakcie półprzewodnika i metalu lub dwóch półprzewodników różnych typów. Działające na tej zasadzie przyrządy nazywamy fotodiodami.

Fotometria. Oświetleniem (energetycznym) E_e powierzchni nazywamy moc promieniowania (strumień energii) padającą na jednostkę tej powierzchni:

gdzie jest mocą promieniowania przypadającą na powierzchnię dS.

Natężeniem promieniowania (źródła) I_e nazywamy moc promieniowania źródła wysyłaną w rozpatrywanym kierunku przypadającą na jednostkę kąta bryłowego:

gdzie jest mocą promieniowania zawartą w kącie bryłowym .

Prawo Lamberta (prawo odwrotnych kwadratów). Prawo to mówi, iż fotonatężenie jest wprost proporcjonalne do odwrotności kwadratu odległości natężenia oświetlenia, czyli:

Gdzie E - natężenie oświetlenia, I - natężenie źródła światła, α - kąt między natężeniem źródła światła, a fotokomórką.

Ponadto dla α=90⁰ natężenie oświetlenia będzie równe zero, gdyż cos90⁰=0. Natomiast dla α=0⁰ natężenie oświetlenia będzie maksymalne.

W naszym ćwiczeniu E będziemy oznaczali jako I, czyli natężenie oświetlenia (fotoprąd).

Przebieg doświadczenia i obliczenia

Układ pomiarowy podłączyliśmy według poniższego schematu

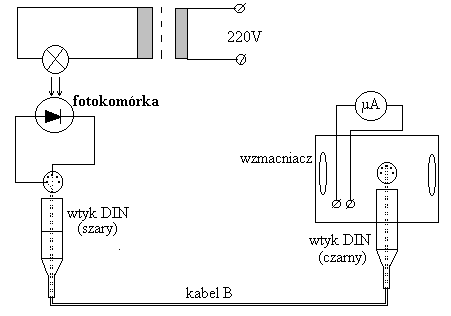
Rys 1.

Następnie wyznaczyliśmy wartość prądu I_0­ w zaciemnionym pomieszczeniu, przy wyłączonym oświetlaczu. I₀=1,3μA.

Ustawiliśmy tak oświetlenie, aby strumień światła oświetlał centrum fotokomórki. Następnie zmieniając odległość r, co 5 cm, oświetlacza od fotokomórki, notowaliśmy zmiany natężenia fotoprądu (I minimalne oraz I maksymalne, dla uzyskania wartości fluktuacji fotoprądu, dla danego r).

Pomiary były prowadzone przy pomocy wzmacniacza prądu o wzmocnieniu równym 80. Mierzony fotoprąd I jest równy:

Gdzie I₀=1,3μA - wskazanie miernika przy wyłączonym oświetlaczu

I_w=(I_min+I­_max)/2 - wskazanie miernika przy włączonym oświetlaczu

Przeskalowany fotoprąd (według wzoru (1)) znajduje się w poniższej tabeli.

Tab 1.

Iśr[μA]	r[cm]	I[μA]
4,15	100	0,035625
4,55	95	0,040625
4,95	90	0,045625
5,55	85	0,053125
6,05	80	0,059375
6,65	75	0,066875
7,45	70	0,076875
8,35	65	0,088125
9,75	60	0,105625
11,55	55	0,128125
13,85	50	0,156875
16,75	45	0,193125
20,65	40	0,241875
26,35	35	0,313125
35,85	30	0,431875
52,25	25	0,636875
85,85	20	1,056875
161,50	15	2,0025

Zależność znajduje się na wykresie 1.

Ocena błędów oraz wnioski

Obliczamy błąd metodą różniczki zupełnej.

Dokładność pomiaru Δr=1cm

r[cm]	3/r^3[cm]
100	0,000003
95	0,000003
90	0,000004
85	0,000005
80	0,000006
75	0,000007
70	0,000009
65	0,000011
60	0,000014
55	0,000018
50	0,000024
45	0,000033
40	0,000047
35	0,000070
30	0,000111
25	0,000192
20	0,000375
15	0,000889

Średni błąd =0,0001

Błędy zostały zaznaczone na wykresie 1.

Odchylenia punktów pomiarowych od oczekiwanych krzywych.

Dodałem linię trendu, typu liniowego. Prosta ta jest położona od punktów pomiarowych na odległość nie większą niż granica błędu. Doskonale to widać na wykresie 1. Przewidywana krzywa teoretyczna to oczywiście linia prosta. Wynika to z prawa Lamberta, które mówi, iż fotonatężenie jest wprost proporcjonalne do odwrotności kwadratu odległości natężenia oświetlenia. Reasumując możemy stwierdzić, iż prawo Lamberta

jest spełnione (jeśli chodzi o związek E z r).

Wyszukiwarka