Adrian Standowicz 13.05.2009

I TM, Aa

Ćwiczenie I: Sprawdzenie II Zasady Dynamiki Newtona dla ruchu obrotowego

1. WSTĘP:

1. 
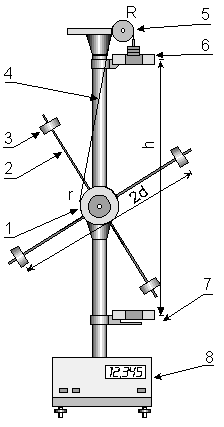
   Wahadło Oberbecka:

Przyrząd umożliwia pośredni pomiar przyspieszenia kątowego układu (krzyżaka z obciążnikami) obracającego się przy różnych ustawianych wartościach momentu bezwładności oraz momentu siły:

• Moment bezwładności układu zmieniamy przesuwając tulejki wzdłuż ramion krzyżaka

• Moment siły zmieniamy, nawijając nitkę na jeden z dwóch krążków, lub zmieniając liczbę ciężarków na szalce obciążnika.

Koło zamachowe (1) wykonane jest w postaci krzyżaka (2), na którego ramionach znajdują się przesuwane tulejki (3) o masie m. Na osi krzyżaka umocowany jest krążek, na który nawinięto nić (4) przerzuconą przez bloczek (5).

Do drugiego końca nici przywiązujemy szalkę z ciężarkami. Podczas opadania szalka z ciężarkami dwukrotnie przecina strumień świetlny złącz optoelektronicznych (6, 7), co powoduje uruchomienie i następnie zatrzymanie cyfrowego stopera (8). Współosiowo z krążkiem (1) osadzony jest hamulec elektromagnetyczny utrzymujący w spoczynku układ krążka, nici i ciężarka. Przejście ciężarka przez dolne złącze optoelektroniczne (7) wyzwala impuls włączający napięcie zasilania elektromagnesu i w konsekwencji zahamowanie ciężarka (a także krążka z krzyżakiem). Drogę opadania ciężarka h (odległość pomiędzy złączami optoelektronicznymi) można zmieniać, a skala przymocowana do kolumny wspornikowej pozwala drogę tę zmierzyć.

2. II Zasada Newtona dla ruchu obrotowego:

Jeżeli na ciało sztywne działa niezrównoważony moment siły, to moment ten nadaje ciału przyspieszenie kątowe, którego wartość jest wprost proporcjonalna do wartości momentu siły i odwrotnie proporcjonalna do momentu bezwładności ciała:

3. Moment siły bryły sztywnej:

Moment siły (moment obrotowy) -
- bryły sztywnej względem osi obrotu O jest sumą iloczynów wektorowych sił
przyłożonych do poszczególnych punktów materialnych bryły oraz promienia wodzącego
, o początku w punkcie O i końcu w punkcie przyłożenia tej siły (lub prościej - sumą momentów sił punktów materialnych tej bryły względem tej osi obrotu):

Wektor momentu siły jest wektorem osiowym (pseudowektorem), zaczepionym w punkcie O, o kierunku prostopadłym do płaszczyzny wyznaczonej przez wektor
i promień wodzący
.

4. Moment bezwładności bryły sztywnej

Moment bezwładności bryły sztywnej, składającej się z n punktów materialnych jest sumą momentów bezwładności wszystkich tych punktów względem obranej osi obrotu:

, gdzie:
- moment bezwładności pojedynczego punktu materialnego

5. Twierdzenie Steinera:

Twierdzenie to mówi, że jeśli znamy moment bezwładności I_o danego ciała względem pewnej osi przechodzącej przez środek masy tego ciała, to aby obliczyć moment bezwładności I względem dowolnej innej osi równoległej do niej, należy do momentu I_o dodać iloczyn masy ciała i kwadratu odległości d między tymi osiami czyli md²:

2. TABELE POMIAROWE:

h = 85cm = 0,85m

2.1. nitka nawinięta na mniejszy bęben:

	ilość ciężarków	m [g]	D1 [cm]	h [m]	t1 [s]	t2 [s]	t3 [s]	t4 [s]	t5 [s]	tśr [s]
1*	2	101,3	1,65	0,85	20,63	18,16	19,85	21,34	19,14	19,824
		4	202,6	1,65	0,85	14,77	15,66	16,5	16,16	16,54	15,926
	2**	2	101,3	1,65	0,85	7,71	7,72	8,02	8,1	8,2	7,95
		4	202,6	1,65	0,85	5,59	5,37	5,54	5,16	5,95	5,522

2.2. nitka nawinięta na większy bęben:

	ilość ciężarków	m [g]	D2 [cm]	h [m]	t1 [s]	t2 [s]	t3 [s]	t4 [s]	t5 [s]	tśr [s]
1*	2	101,3	3,25	0,85	9,94	9,53	10,92	9,7	10,17	10,052
		4	202,6	3,25	0,85	6,93	6,72	7,08	6,98	7,09	6,96
	2**	2	101,3	3,25	0,85	3,73	3,82	4,13	3,94	3,9	3,904
		4	202,6	3,25	0,85	2,8	2,56	2,86	2,74	2,88	2,768

* 1 - ciężarki C na końcach prętów wahadła

** 2 - ciężarki C jak najbliżej osi obrotu

3. OBLICZENIA:

3.1. przykład dla pierwszego pomiaru z tabeli 2.1.:

Przyspieszenie liniowe:

Przyspieszenie kątowe:

Moment siły działający na bęben:

Moment bezwładności wahadła:

Zestawienie wyników (liczone z użyciem średniej wartości mierzonych czasów):

3.2. nitka nawinięta na mniejszy bęben:

	ilość ciężarków	a [m/s^2]	ε [1/s^2]	M [Nm]	I [kg·m]
1*	2	0,004	0,524	0,008	0,016
		4	0,007	0,812	0,016	0,02
	2**	2	0,027	3,260	0,008	0,0025
		4	0,056	6,758	0,016	0,0024

3.3. nitka nawinięta na większy bęben:

	ilość ciężarków	a [m/s^2]	ε [1/s^2]	M [Nm]	I [kg·m]
1*	2	0,017	1,035	0,0161	0,01557
		4	0,035	2,159	0,0322	0,01490
	2**	2	0,111	6,863	0,0159	0,00233
		4	0,222	13,654	0,0316	0,00231

4. RACHUNEK BŁĘDU (metodą Studenta-Fishera):

t_5,0.9 = 2,312

4.1. Przykładowe obliczenia

Wyliczamy wartości konkretnej wielkości np. przyspieszenia liniowego a:

	t1 [s]	t2 [s]	t3 [s]	t4 [s]	t5 [s]	tśr [s]
a [m/s^2]	0,00399	0,00515	0,00431	0,00373	0,00464	0,00433

Dla obliczonych wartości liczymy błąd studenta, w następujący sposób:

Zestawienie wyników rachunku błędu:

4.2. nitka nawinięta na mniejszy bęben:

- dla przyspieszenia liniowego a:

	ilość ciężarków
1*	2	0,00025	0,00058
		4	0,00029	0,00068
	2**	2	0,00068	0,0016
		4	0,0026	0,0061

- dla przyspieszenia kątowego ε:

	ilość ciężarków
1*	2	0,03	0,07
		4	0,036	0,082
	2**	2	0,083	0,192
		4	0,318	0,735

- dla momentu siły M:

	ilość ciężarków
1*	2	2,09E-07	4,83E-07
		4	4,91E-07	1,14E-06
	2**	2	5,71E-07	1,32E-06
		4	4,38E-06	1,01E-05

- dla momentu bezwładności I:

	ilość ciężarków
1*	2	0,00088	0,002
		4	0,00082	0,0019
	2**	2	6,32E-05	0,00015
		4	0,00012	0,00027

4.3. nitka nawinięta na większy bęben:

- dla przyspieszenia liniowego a:

	ilość ciężarków
1*	2	0,00085	0,0018
		4	0,00069	0,0016
	2**	2	0,0038	0,0087
		4	0,0098	0,0228

- dla przyspieszenia kątowego ε:

	ilość ciężarków
1*	2	0,048	0,110
		4	0,043	0,099
	2**	2	0,232	0,535
		4	0,606	1,400

- dla momentu siły M:

	ilość ciężarków
1*	2	1,28E-06	2,95E-06
		4	2,29E-06	5,29E-06
	2**	2	6,19E-06	1,43E-05
		4	3,24E-05	7,49E-05

- dla momentu bezwładności I:

	ilość ciężarków
1*	2	0,00077	0,0018
		4	0,00029	0,00066
	2**	2	8,14E-05	0,00019
		4	9,64E-05	0,00022

5. WNIOSKI:

Ćwiczenie to pozwoliło nam na zbadanie zależności wartości przyspieszenia kątowego układu (ε) od wartości momentu siły (
) i momentu bezwładności I. Doszliśmy do wniosku, że im większy moment siły zostanie przyłożony do układu, tym szybciej układ zwiększa swoją prędkość obrotową (przyspieszenie kątowe wzrasta). Z kolei zwiększanie momentu bezwładności układu ma skutek odwrotny - zmniejsza przyspieszenie kątowe układu spowalniając wykonywany przez niego ruch obrotowy.

Jak w każdym doświadczeniu należało jednak liczyć na pojawienie się błędów. Głównym źródłem błędu w ćwiczeniu była wada konstrukcyjna krzyżaka, który nie był do końca symetryczny względem osi obrotu. Powodowało to nierówny rozkład mas, przez co urządzenie potrzebowało więcej czasu aby się „rozpędzić”. Innymi źródłami błędu mogły być czynniki takie jak:

- błędy odczytu czasu przecięcia linii pomiarowych przez spadającą masę.

- stosunkowo gruba linka

- tarcie i opór powietrza

- błąd pomiarowy wagi, którą mierzyliśmy masę odważników wieszanych na lince

Itp.

SPRAWOZDANIE

---