Politechnika Częstochowska

Instytut Fizyki

Ćwiczenie numer 13

Wyznaczanie odległości ogniskowych soczewek metodą Bessela

Krzysztof Bolingier

Łukasz Czekała

Rok 1999/2000

Inżynieria Środowiska

Grupa I

Częstochowa 2000

1. Własności soczewek skupiających i rozpraszających.

Soczewkami nazywamy ciała przezroczyste ograniczone dwiema powierzchniami, lub jedna powierzchnią płaską i jedną zakrzywioną. Ze względu na kształt rozróżniamy: dwuwypukłe, dwuwklęsłe, płaskowypukłe, płaskowklęsłe, wklęsłowypukłe i wypukłowklęsłe.

Własności soczewek skupiających:

• Promienie równoległe do głównej osi optycznej po przejściu przez soczewkę skupiającą przecinają się w jednym punkcie, zwanym ogniskiem soczewki, położonym na głównej osi optycznej.

• Odległość ogniska od soczewki, zwana odległością ogniskową soczewki f, określona jest wzorem soczewkowym:
  ; gdzie n - jest współczynnikiem załamania materiału soczewki względem ośrodka otaczającego.

• Soczewka skupiająca wytwarza rzeczywiste obrazy przedmiotów położonych w odległości x > f na głównej osi optycznej i pozorne obrazy przedmiotów położonych w odległościach x < f.

• Odległość x przedmiotu od soczewki i odległość y obrazu od soczewki powiązane są równaniem soczewki
  . Przyjmuje się umowę, że odległości obrazów pozornych od soczewki są ujemne.

Własności soczewek rozpraszających:

• Promienie równoległe do głównej osi optycznej soczewki odchylają się po przejściu przez soczewkę tak, że ich przedłużenia przecinają się w ognisku pozornym - punkcie położonym na głównej osi optycznej przed soczewką.

• Ogniskowej f soczewki rozpraszającej przypisujemy umownie wartość ujemną. Ogniskowa ta określana jest także wzorem soczewkowym.

• Soczewka rozpraszająca wytwarza obrazy pozorne przedmiotów położonych na głównej osi optycznej.

• Odległości przedmiotu x i obrazu y od soczewki spełniają równanie soczewki.

2. Równanie soczewki cienkiej
   

Zależność odległości f od promieni krzywizn oraz od współczynnika załamania n materiału, z którego sporządzona jest soczewka, określana jest powyższym równaniem.

Promienie wychodzące z dowolnego punktu A, w skutek ich załamania w soczewce, zostają zebrane w innym punkcie B, (jeśli soczewka jest cienka, a promienie tworzą niewielki kąt z osią główną). Punkt B jest obrazem punktu A. Jeżeli przedmiot A składa się z wielu punktów, wysyłających światło, to każdemu z nich można przyporządkować odpowiedni punkt obrazu.

We wzorze r₁ i r₂ oznaczają promienie okręgów, z których została zbudowana soczewka, zwanymi także promieniami sferycznymi, f - jest to odległość ogniskowa, czyli odległość od środka optycznego soczewki.

3. Otrzymywanie obrazów za pomocą soczewki.

Położenie i wielkość obrazu wytwarzanego przez soczewkę można określić metodą geometryczną. Dla uproszczenia przedstawiamy schematycznie przedmiot w postaci strzałki prostopadłej do głównej osi optycznej. Do konstrukcji obrazu wystarczy określić położenie obrazu punktu stanowiącego wierzchołek strzałki, rysując dwa wyróżnione promienie rozchodzące się z tego punktu.

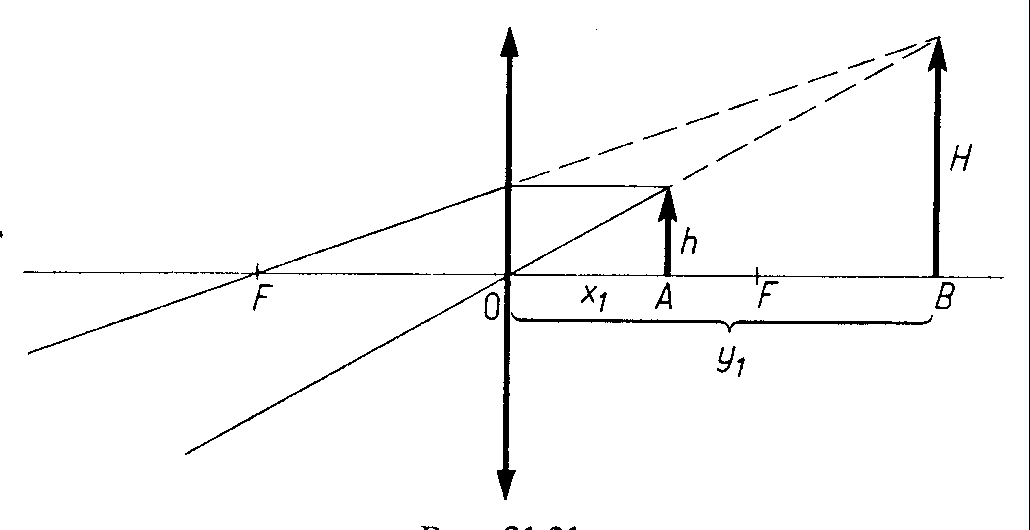
Na rysunku przedstawiony jest przebieg promieni odpowiadający powstaniu pozornego obrazu dla przedmiotu ustawionego na prawo od soczewki skupiającej. Przedmiot o wysokości h, ustawiony w odległości x₁ > 0, daje obraz pozorny o wysokości H w odległości y₁ < 0. Z zasady odwracalności biegu promieni wynika, że rysunek ten opisuje także sytuację, gdy na soczewkę skupiającą pada z lewej stron zbieżna wiązka promieni. Gdyby nie było soczewki, wiązka ta wytworzyłaby obraz rzeczywisty o wysokości H w punkcie B. W rzeczywistości obraz powstaje w punkcie A i ma wysokość h. Obraz, który powstałby w punkcie B, gdyby nie było soczewki nazywamy przedmiotem pozornym. Dla soczewki skupiającej obrazy przedmiotów pozornych są zawsze rzeczywiste. W soczewkach rozpraszających mogą powstać zarówno pozorne, jak rzeczywiste obrazy pozornych przedmiotów. Obrazy rzeczywiste pozornych przedmiotów są zawsze proste, a obrazy pozorne pozornych przedmiotów są odwrócone.

Dyskusja wzoru:

Odległość x przedmiotu od soczewki związana jest z odległością y obrazu od soczewki równaniem dla soczewek cienkich:
. Dla x → ∞, ¹/_x → 0, a więc y = f. Promienie biegnące z nieskończoności są równoległe. Gdy przedmiot zbliża się do soczewki, x staje się mniejsze; ponieważ prawa strona równania pozostaje niezmieniona, wobec tego y musi rosnąć. Przedmiot i jego obraz poruszają się w tę samą stronę. Dla x = 2f zachodzi zależność:

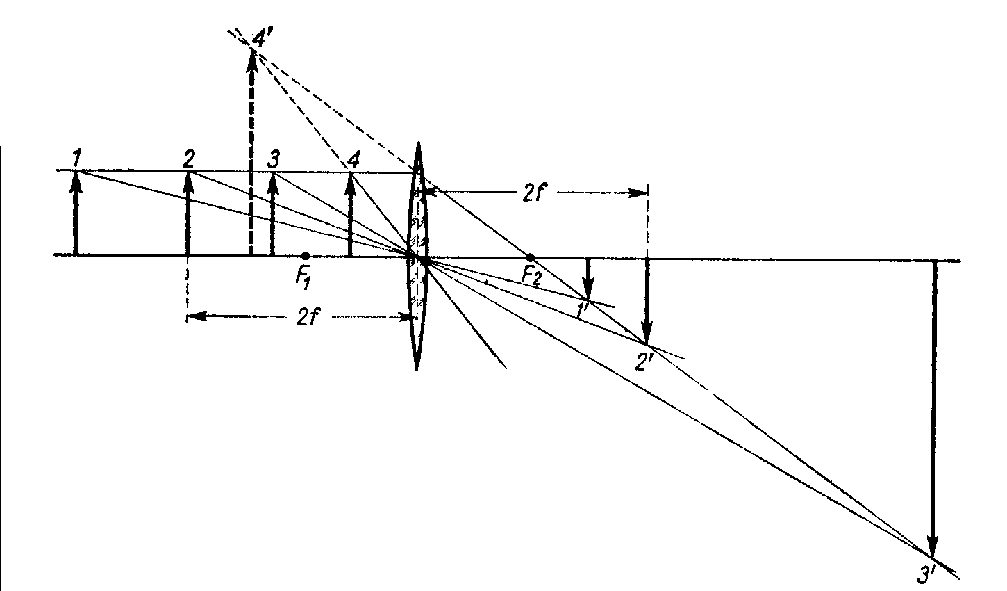
, a więc y = 2f, co oznacza, że odległości przedmiotu i obrazu od soczewki są jednakowe, a wielkości przedmiotu i obrazu są również takie same. Gdy przedmiot przesuwa się, od 2f do f, wtedy obraz odsuwa się od soczewki, gdy zaś x = f - oddala się do nieskończoności. Promienie wychodzące z ogniska po przejściu przez soczewkę biegną jako wiązka równoległa do osi głównej. Jak długo x > f, otrzymujemy obrazy rzeczywiste i odwrócone. Gdy zaś x < f, dla y otrzymujemy wartość ujemną. Powstaje wówczas obraz urojony i prosty, położony po tej samej stronie soczewki, co i przedmiot.

4. Zdolność zbierająca soczewek i układu soczewek.

Zdolność zbierająca D soczewek wyrażamy odwrotnością ogniskowej f liczonej w metrach D = ¹/_f. Jednostką zdolności zbierającej jest dioptria; soczewka o ogniskowej f = 1 m ma zdolność zbierającą równą 1 dioptrii. Im krótsza jest ogniskowa f soczewki, tym większa jest jej zdolność zbierająca.

W praktyce często są stosowane układy złożone z kilku soczewek działające w ten sposób, że promienie po przejściu przez jedną z nich są skierowane na następną. Można wykazać, że w przypadku soczewek cienkich, umieszczonych blisko siebie zdolność zbierająca układu ¹/_f jest równa sumie algebraicznej zdolności zbierającej jego poszczególnych soczewek:

lub

5. Metody wyznaczania ogniskowych soczewek skupiających i rozpraszających ze szczególnym uwzględnieniem metody Bessela.

W równaniu soczewek odległość x i y (przedmiotu i obrazu od soczewki) są zmienne, tzn. przy stałej odległości l przedmiotu od ekranu istnieją dwie pozycje soczewki, przy których otrzymujemy ostry obraz na ekranie - raz powiększony, drugi raz zmniejszony. Obie sytuacje różnią się między sobą tym, że odległość x i y zmieniają się rolami: odległość x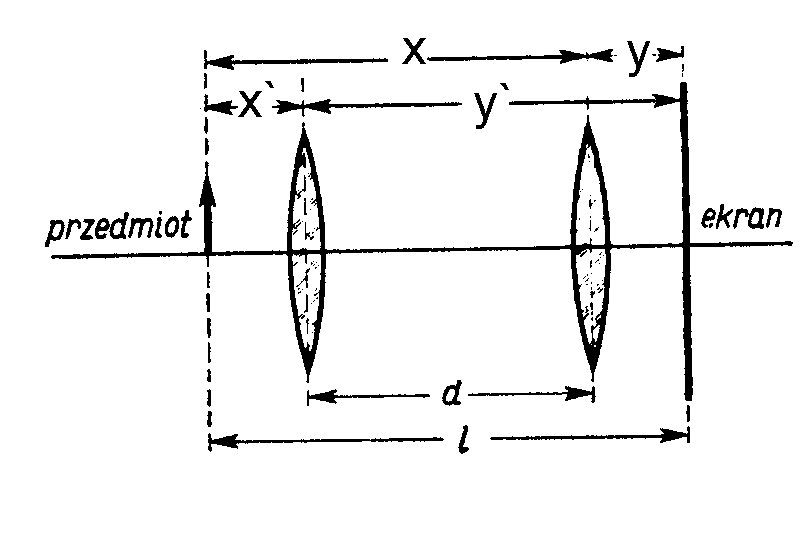
przedmiotu w jednej pozycji staje się odległością y obrazu, i odwrotnie. Odczytujemy odległość d między obu pozycjami soczewki. W tym przypadku obojętne jest względem, jakiego punktu odniesienia odczytamy odległości między soczewkami, zawsze ona będzie taka sama. Ponieważ obie pozycje są symetryczne, a więc x = y` i y = x`; mamy stąd x + y = l oraz x - y = d. Dodając oraz odejmując oba ostatnie równania stronami otrzymujemy x=¹/₂(l+d), y = ¹/₂ (l - d). Znalezione wartości x i y podstawiamy do równania soczewek otrzymując wzór na

f:

Wyznaczenie f na podstawie odległości przedmiotu i obrazu od soczewki. Mając zmierzone odległości x i y możemy wyznaczyć f posługując się wzorem wyprowadzonym z równania soczewki:
. Do pomiarów używamy ławy optycznej. Soczewkę ustawiamy tak, by na ekranie ukazał się ostry obraz. Oszacowanie ostrości jest obarczone dużą niepewnością, więc ustawienie soczewek powtarzamy kilkakrotnie, po czym wyznaczamy wartość średnią pozycji wskaźnika. Wyniki pomiarów obejmują, co najmniej cztery pomiary dla obrazu powiększonego i cztery dla obrazu zmniejszonego. Po obliczeniu f (ze wzoru) dla każdego z pomiarów, znajdujemy jej wartość średnią f.

Tabela pomiarowa

Soczewka	d [m]	a1 [m]	a2 [m]	l= a1- a2 [m]	f [m]
1	0,57	0,46	0,134	0,326	0,0958877
2	1,153	0,998	0,190	0,808	0,14669232
3	1,297	0,859	0,474	0,385	0,29567925
Układ soczewek 1, 4	0,65	0,372	0,218	0,154	0,153378

d - odległość przedmiotu rzutowanego od ekranu

a₁ - odległość soczewki od ekranu, gdy na ekranie powstał obraz powiększony

a₂ - odległość soczewki od ekranu, gdy na ekranie powstał obraz pomniejszony

l - różnica odległości, między położeniami soczewek, kiedy obraz był powiększony a pomniejszonym

f - ogniskowa soczewek używanych do przeprowadzania ćwiczenia

6. Wyniki.

7. Błędy.

Błędy mogące wystąpić w naszym ćwiczeniu to błędy systematyczne i przypadkowe:

• Błędy wynikające z niedokładności stosowanych przyrządów.

• Błędy operatywne, przy małej praktyce laboratoryjnej

• Błędy wynikające z autosugestii laboranta

• Zmęczenie laboranta

• Chwilowe zmniejszenie naszej uwagi

Błąd względny

-6-

---