POLITECHNIKA CZĘSTOCHOWSKA
KATEDRA FIZYKI
LABORATORIUM
PODSTAWY FIZYKI WSPÓŁCZESNEJ
Ćwiczenie nr 13
TEMAT: Wyznaczanie odległości ogniskowych soczewek metodą
Bessela.
Wydział: Budowa Maszyn
Kierunek: Informatyka
Rok II Grupa II
Pisały: Monika Kołodziejczyk
Anna Koperska
Data: 14.X.1999r.
I. Zagadnienia: |
|
2. Równanie soczewki cienkiej
|
|
4. Zdolność zbierająca soczewek i układu soczewek. |
5. Metody wyznaczania ogniskowych soczewek skupiających i rozpraszających ze szczególnym uwzględnieniem metody Bessela.
|
Ad.1
Soczewką nazywamy bryłę przeźroczystego materiału, ograniczoną dwoma powierzchniami sferycznymi, których środki krzywizny leżą na osi, zwanej osią optyczną soczewki. Każdy promień świetlny ulega dwukrotnie załamaniu na powierzchniach ograniczających soczewkę. Na rysunku załamanie dwukrotne zastępujemy jednokrotnym załamaniem na tzw. powierzchni środkowej , czyli powierzchni prostopadłej do osi optycznej przechodzącej przez środek geometryczny soczewki. Wiązka promieni biegnących równolegle do osi optycznej soczewki zbierającej, po przejściu przez soczewkę skupia się w jednym punkcie, zwanym ogniskiem. W soczewce rozpraszającej w ognisku przecinają się przedłużenia promieni przechodzących. Odległość ogniska od powierzchni środkowej nazywamy ogniskową soczewki. Promień biegnący pod dowolnym kątem względem osi optycznej nie ulega załamaniu tylko wtedy, gdy przechodzi przez punkt, zwany środkiem optycznym soczewki. Soczewkę nazywamy cienką, gdy jej grubość jest mała w porównaniu z promieniem krzywizny.
Soczewka skupiająca - soczewka zbierająca, soczewka dodatnia; soczewka charakteryzująca się tym, że wiązka promieni po przejściu przez nią zwiększa swą zbieżność. Soczewki skupiające mają ogniskowe dodatnie, a grubość w pojedynczych soczewkach jest mniejsza na brzegu niż w środku. Rozróżnia się proste soczewki: dwuwypukłe, płasko - wypukłe, wypukło - wklęsłe.(rys. 1).O własnościach soczewek skupiających decyduje jej moc optyczna. Cienką soczewkę skupiającą zaznacza się na rysunku symbolem (rys. 2).
a) b) c)
Rys. 1. Soczewka skupiająca: a) dwuwypukła, b) płasko-wypukła, c) wypukło-wklęsła
1
2
3
F F
Rys. 2. Bieg promieni w soczewce skupiającej
Otrzymany obraz wykreśla się przez narysowanie dwóch z trzech promieni, poprowadzonych z danego punktu przedmiotowego: 1 - równoległego do osi, 2 - przechodzącego przez ognisko przedmiotowe, 3 - przechodzącego przez środek soczewki. Soczewki skupiające stosuje się prawie we wszystkich układach optycznych.
Soczewka rozpraszająca - soczewka ujemna; soczewka charakteryzująca się tym, że wiązka promieni po przejściu przez nią zmniejsza swą zbieżność. Pojedyncze soczewki rozpraszające mają ogniskowe ujemne, a grubość na brzegu jest większa niż w środku (rys. 1). Rozróżnia się proste soczewki rozpraszające: dwuwklęsłe, płasko-wklęsłe, wklęsło-wypukłe. Cienką soczewkę rozpraszającą przedstawia się graficznie w postaci
.
a) b) c)
Rys. 1. Rodzaje soczewek rozpraszających: a)dwuwklęsła, b)płasko-wklęsła c)wklęsło-wypukła
Położenie obrazu w cienkiej soczewce rozpraszającej wyznacza się analogicznie, jak w soczewce zbierającej (rys. 2) Soczewki rozpraszające stosuje się w licznych układach optycznych, przede wszystkim do poprawy chromatyzacji, zmniejszenia krzywizny pola oraz do zwiększenia odległości przedmiotu (obrazu) od układu.
A
A'
F F
Rys. 2. Wykreślanie obrazu w soczewce cienkiej
Ad.2
Równanie soczewki cienkiej.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Punkty ![]()
i![]()
oznaczają środki krzywizn obu powierzchni soczewki. Prosta, która je łączy przechodzi przez środek soczewki i stanowi oś główną soczewki. Promień AM tworzy z osią główną mały kąt ![]()
. W punkcie padania promienia na soczewkę prowadzimy płaszczyznę styczną i normalną M![]()
. Przechodząc do ośrodka optycznie gęstszego promień załamuje się i pada w punkcie N na drugą powierzchnię soczewki, tutaj również prowadzimy płaszczyznę styczną i normalną N![]()
. Obie normalne są niczym innym jak promieniem krzywizny odpowiedniej powierzchni soczewki. Promień załamany przecina oś główną w punkcie B.
Płaszczyzny styczne do powierzchni soczewek poprowadzone w punktach M (padania) i N (wyjścia) promienia AM, tworzą ściany boczne zastępczego pryzmatu o kącie łamiącym ![]()
. Ten sam kąt tworzą normalne M![]()
i N![]()
. Jest to jednocześnie kąt zewnętrzny w trójkącie ![]()
C ![]()
. Możemy więc zapisać równość : ![]()
Jednocześnie kąt ![]()
jest kątem zewnętrznym trójkąta AEB, gdzie punkt E tworzą przedłużenia promienia wchodzącego i wychodzącego z pryzmatu, czyli:
![]()
Dzięki założeniu, że kąty ![]()
i kąt padania promienia AM są małe, można zastosować wzór :
![]()
; gdzie n jest współczynnikiem załamania naszego zastępczego pryzmatu .
Otrzymujemy więc : ![]()
(*)
Wobec tego, że kąty są małe, możemy je zastąpić ich sinusami lub tangensami. Z założenia, że soczewka jest cienka wynika, że wysokości punktów M i N nad osią główną są sobie w przybliżeniu równe : MD ≈ NG = h
A zatem oznaczając odległość przedmiotu od soczewki przez x, a odległość obrazu od soczewki przez y mamy:
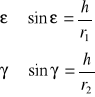
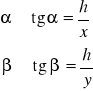
Podstawiając do (*) ,otrzymujemy : 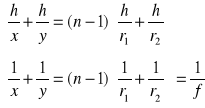
f - ogniskowa soczewki.
1/f - zdolność skupiająca soczewki.
Przyjmuje się, że ogniskowa a więc i zdolność skupiająca soczewki skupiającej jest dodatnia, rozpraszającej zaś ujemna.
n - współczynnik załamania materiału, z którego wykonana jest soczewka względem
otaczającego ją ośrodka.
r1 - promień krzywizny pierwszej powierzchni soczewki.
r2 - promień krzywizny drugiej powierzchni soczewki.
Promień krzywizny soczewki jest dodatni, jeśli środek krzywizny tej powierzchni leży po przeciwnej stronie soczewki niż przedmiot, ujemny w przeciwnym przypadku.
Ad.3
Dyskusja wzoru soczewkowego. Otrzymywanie obrazów za pomocą soczewek.
Wprowadzając pojęcie ogniskowej soczewki otrzymaliśmy wzór dla soczewek cienkich w postaci :
![]()
Wobec identycznej postaci tego wzoru z wzorem dla zwierciadeł kulistych otrzymujemy te same wyniki dyskusji, trzeba jednak pamiętać, że nie obowiązuje zależność f=r/2 .
W odniesieniu do soczewek należy rozwiązać następujące odległości x: x>2f , x=2f , x zawarte między f i 2f , x=f , x<f . W związku z tym wygodnie jest uwzględniać na osi głównej dodatkowy punkt „2F”, leżący w odległości równej 2f od soczewki.
Położenie punktu świecącego względem ogniska lub punktu „2F” decyduje o charakterze otrzymywanego obrazu. Wyniki dyskusji ilustruje poniższe zestawienie.
1) Soczewka skupiająca
(a) Przypadek x > 2f (b) Przypadek 2f > x > f (c) Przypadek f > x >0
b
B F F B
S a S a S
A 2F F 2F F 2F a A
b
b
Otrzymamy obraz : Otrzymamy obraz : Otrzymamy obraz :
rzeczywisty, odwrócony, rzeczywisty, odwrócony, pozorny, prosty,
pomniejszony powiększony powiększony
2) Soczewka rozpraszająca
(a) Przypadek x > 2f (b) Przypadek 2f > x > f (c) Przypadek f > x > 0
B B B
b
b b
S S S
A a A a A a
W każdym z tych przypadków otrzymujemy obraz pozorny, prosty i pomniejszony.
Jeżeli przez „S” oznaczymy środek optyczny soczewki to z podobieństwa trójkątów ABS i Sab wynika bezpośrednio wzór na powiększenie liniowe soczewki :
![]()
Im dalej od soczewki tworzy się obraz, tym jego rozmiary poprzeczne są większe .
Ad.4
Zdolność zbierająca soczewek i układu soczewek.
Zdolność skupiająca soczewki jest odwrotnością jej ogniskowej wyrażonej w metrach .
![]()
Z=[D]=[1/m] -dioptria
Jedna dioptria jest to zdolność skupiająca soczewki ogniskowej 1 metra. Zdolność skupiająca układu soczewek jest równa zdolności skupiającej soczewek tworzących ten układ.
![]()
![]()
.
Ad.5
Metody wyznaczania ogniskowych soczewek skupiających i rozpraszających.
1.Pomiar ogniskowej wykorzystujący równanie soczewkowe.
Korzystając z ławy optycznej dobieramy warunki w ten sposób, by na ekranie uzyskać obraz powiększony znanego przedmiotu. Przedmiotem jest nieprzezroczysty ekran z otworem (w kształcie np. litery), przysłonięty szkłem matowym. Soczewkę badaną i ekran ustawiamy na ławie optycznej. Położenie soczewki dobieramy tak, by uzyskać obraz powiększony i wykonujemy pomiar odległości x i y. Obliczamy ogniskową z równania 1/x + 1/y = 1/f . Pomiar może być obarczony błędem systematycznym, ponieważ nie znamy dokładnie położenia optycznego soczewki.
2.Metoda Bessela.
Występujące we wzorze 1/x + 1/y = 1/f wielkości x i y możemy zamienić. W rzeczywistości zamianie odpowiada takie przesunięcie przy stałej odległości przedmiotu i ekranu, by odległość wynosiła x, odległość zaś przedmiotu y. Z rysunku numer 1 wynika, że x + y = d oraz x - y = l. Obliczam stąd x i y, a następnie podstawiamy do wzoru 1/x + 1/y = 1/f , otrzymując
f = (d*d -l*l)/4d
Pomiar sprowadza się do wyznaczenia położenia a[1] soczewki, przy którym uzyskujemy obraz powiększony, oraz położenia a[2] -dla obrazu pomniejszonego. Wartości l = a[1] + a[2] oraz odległość d przedmiotu i ekranu podstawiamy do wzoru
f = (d*d -l*l)/4d
a'=a b'=b
e
E A
O1 Z
A2 d p O
A1
b a
l
Rys. 1. Zasada wyznaczania ogniskowych soczewek metodą Bessela.
3. Zastosowanie lunety.
Wiązka światła wybiegająca z ogniska po przejściu przez soczewkę jest wiązką równoległą. Dla przedmiotu ustawionego w ognisku nie otrzymuje się obrazu na ekranie. Obraz ten uzyskać możemy za pomocą lunety nastawionej na nieskończoność. W celu wykonania pomiaru nastawiamy lunetę na ostrość widzenia odległego punktu, ustawiamy ją na miejsce ekranu i dobieramy położenie soczewki
w ten sposób, by uzyskać w lunecie ostry obraz przedmiotu lub jego fragmentu. Mierzymy odległość przedmiotu od soczewki. (rys. 2).
S
P L
oko
f
Rys. 2. Wyznaczanie ogniskowej soczewki za pomocą lunetki.
II. Obliczenia:
1.Wyznaczając ogniskową soczewki korzystamy z zależności:
a) soczewka nr 1
d=735mm ; l=(500+498+499)/3=499mm ;
czyli f1=(540225-249001)/2940=291224/2940=99,05≈99,1mm
b) soczewka nr 2
d=980mm ; l=(520+525+524)/3=523mm ;
czyli f2=(960400-273529)/3920=686871/3920=175,22≈175,2mm
c) soczewka nr 3
d=1575mm ; l=(785+780+783)/3=782,66mm ;
czyli f3(2480625-612556,67)/6300=1868068,33/6300=296,52≈296,5mm
d) soczewki 1 i 4 (fu)
d=1475mm ; l=(910+910+900)/3=906,66mm ;
czyli fu=(2175625-822032,35)/5900=1353592,65/5900=229,42≈229mm
Na podstawie tego obliczamy ogniskową soczewki nr 4.
Korzystając z zależności:
Ostatecznie: f4=(229,42*99,05)/(229,42-99,05)=22724,05/130,37=174,30≈174mm
2. Wyznaczając błąd odległości ogniskowych Δf wykorzystujemy metodę różniczki
zupełnej.
Ostatecznie:
a) wyznaczenie Δf1
d=735mm ; l=499mm ; Δd=1mm ; Δl=2mm
Δf1=(540225+249001)/2160900+-499/1470*2=0,36+0,68=1,04≈1,1mm
b) wyznaczenie Δf2
d=980mm ; l=523mm ; Δd=1mm ; Δl=2mm
Δf2=(960400+273529)/3841600+-523/1960*2=0,32+0,54=0,86≈0,9mm
c) wyznaczenie Δf3
d=1575mm ; l=782,66mm ; Δd=1mm ; Δl=2mm
Δf3=(2480625+612556,67)/9922500+-782,66/3150*2=
= 0,31+0,5=0,81≈0,9mm
d) wyznaczenie Δfu
d=1475mm ; l=906,66mm ; Δd=1mm ; Δl=2mm
Δfu=(2175625+822032,35)/8702500+-906,66/2950*2=
=0,34+0,62=0,96≈1mm
Δf4=(Δfu*Δf1)/(Δfu-Δf1)=(0,96*1,04)/(0,96-1,04)=
=0,9984/(-0,08)=12,48≈13mm
III. Wnioski:
Na pocz --> [Author:p] ątku niniejszego ćwiczenia szacowałyśmy orientacyjnie ogniskową soczewki nr 1, umieszczając ją na ławie optycznej między kolimatorem, a ekranem i szukając takiej odległości ekranu od soczewki aby otrzymać ostry obraz źródła światła. Odległość ta w przybliżeniu ≈f. Wykonaliśmy to samo dla wszystkich soczewek otrzymując wyniki, które wpisywałyśmy do tabeli pomiarowej. Oczywiście oszacowanie obarczone jest dużą niepewnością, jednak przy błędzie odległości ogniskowych Δf, który wyznaczony przez nas balansuje wokół 1mm, rzeczywiście różnice wydają się duże. Przyczyny tego leżą po obu stronach: z jednej strony jest niepewność oszacowania, z drugiej natomiast błędne być może założenie, które przyjęłyśmy. Co do wielkości Δd i Δl (Δd przyjęłyśmy 1mm, a Δl=2mm). Jeżeli te dwa błędy będą miały większe wartości, to automatycznie większa będzie wartość błędu Δf, co zmniejszy nieco różnice powstałe wskutek oszacowania i pomiarów.
ąc vcź
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
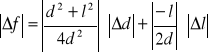
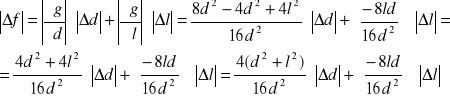
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Opt- Wyznaczanie odległości ogniskowych soczewek metodą Bess(1), Sprawozdania - Fizyka
Opt- Wyznaczanie odległości ogniskowych soczewek metodą Be(1, Sprawozdania - Fizyka
WYZNACZANIE ODLEGŁOŚCI OGNISKOWYCH SOCZEWEK METODĄ BESSELA, Sprawozdania - Fizyka
OPT- wyznaczanie odległości ogniskowych soczewek metodą bess, Sprawozdania - Fizyka
Wyznaczanie odległości ogniskowych soczewek metodą?ssela
sprawozdanie O7. Wyznaczanie odległości ogniskowych soczewek, pśk inżynieria środowiska 1 rok, fizyk
Cw 06 - Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego i metodą Bessela, Sprawozdania fizyka
Wyznaczanie ogniskowej soczewki metodą Bessela, Sprawozdania
Wyznaczanie odległości ogniskowych soczewek
Wyznaczanie bezwzglednego wspolczynnika lepkosci metoda Stokesa - sprawozdanie, Fizyka
Wyznaczanie odległości ogniskowych soczewek
Wyznaczenie odległości ogniskowych metodą Bessela, Sprawozdania - Fizyka
Ćw. 6 Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego i metodą Bessela, PWSZ, Fizyka laborki
POMIAR ODLEGŁOŚCI OGNISKOWYCH SOCZEWEK1, Studia - podręczniki, fizyka, sprawozdania, soczewki, badan
Pomiar odległości ogniskowych soczewek, Pwr MBM, Fizyka, sprawozdania vol I, sprawozdania część I
Wyznaczanie ogniskowej soczewki metodą Bessela, Technologia chemiczna, semestr 2, Fizyka, Laboratori
PIOTREK K WYZNACZANIE OGNISKOWEJ SOCZEWKI METODA BASSELA, studia, Budownctwo, Semestr II, fizyka, Fi
więcej podobnych podstron