LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW.	Imię i nazwisko: Dwurnik Krzysztof
	Nr ćwiczenia: 3	Data wykonania: 15.02.00		Data zaliczenia:
Temat ćwiczenia: TENSOMETRIA OPOROWA.	Ocena za sprawozdanie:		Ocena za kolokwium zaliczeniowe:

1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z techniką pomiaru odkształceń za pomocą rozet tensometrycznych oraz wyznaczenie kierunków i wartości głównych odkształcenia na powierzchni elementu przestrzennego.

2. Budowa stanowiska pomiarowego.

Stanowisko pomiarowe składa się ze zginanej płyty, w której wykonano kilka otworów, umieszczonych na jej powierzchni dwu rozet tensometrycznych R₁ i R₂ oraz mostka tensometrycznego i układu rejestrującego.

3. Tensometria oporowa.

Tensometria zajmuje się metodami pomiarów odkształceń, „deformacji”. Każda rzeczywista konstrukcja po obciążeniu zmienia swoje kształty-deformując się , a każdy (dowolny) jej punkt A przemieszcza się o pewien wektor u i przyjmuje położenie A'. Wektor u jest funkcją x≡{x₁,x₂,x₃}, a więc tworzy pole wektorowe które nazywamy polem przemieszczeń. Obiekt geometryczny, który pozwala wzajemnie odwzorować otoczenia przed i po deformacji nazywamy - tensorem odkształcenia. Zawiera on w sobie wszystkie informacje o zmianach kształtów tych otoczeń. Dla małych odkształceń:

gdzie: dso -moduł nieskończenie małego wektora dso z otoczenia nie zdeformowanego (wektor dso jest współliniowy z wektorem n o współrzędnych n_k k=1,2,3 modn=1);

ds. -moduł wektora ds. w który to wektor odwzorowuje się wektor dso po zdeformowaniu się otoczenia.

Iloraz po prawej stronie można interpretować jako względną zmianę długości odcinka dso (z otoczenia wokół punktu x ) o kierunku określonym wektorem jednostkowym co możemy zanotować np. w formie:

Wielkość ε⁽ⁿ⁾ jest często nazywana wydłużeniem właściwym elementu liniowego dso. Doświadczalnie (z pewnym przybliżeniem) można tę wielkość mierzyć przy pomocy tensometrów. Jeśli baza tensometru ma długość Δso to mierzona wartość ε⁽ⁿ⁾ będzie uśredniona na tej długości i wyniesie:

Będzie ona równa wartości w nieskończenie małym otoczeniu punktu tylko wtedy gdy na Δso wystąpi jednorodny stan odkształcenia.

W praktyce laboratoryjnej pomiary odkształceń ograniczają się najczęściej do powierzchni konstrukcji. Wynika to bezpośrednio z charakteru przyrządów pomiarowych - tensometrów, jak również z faktu, iż eksperymentalne wartości odkształceń „naprężeń” występują zazwyczaj na powierzchni ciała. Zespół tensometrów mierzących wydłużenia właściwe typu ε⁽ⁿ⁾ równocześnie w kilku kierunkach tego samego otoczenia punktu tworzy Rozetę tensometryczną. Mierząc wartości ε⁽ⁿ⁾ w kilku dowolnie wybranych kierunkach n tego otoczenia (na powierzchni i,j=1,2 3różne kierunki n) ze wzoru

ε⁽ⁿ⁾ =n_in_j

można wyznaczyć wszystkie współrzędne ε_ij

Tensometry stosowane w badaniach odkształceń elementów konstrukcyjnych, ze względu na zasadę działania pomiaru, dzielimy na dwie grupy:

a)elektryczne

b)mechaniczne.

W pierwszej grupie wyróżniamy tensometry: rezystancyjne, zwane również oporowymi, indukcyjne, pojemnościowe, elektrodynamiczne i piezoelektryczne. W drugiej natomiast tensometry: mechaniczne optyczno - mechaniczne i strunowe.

Metoda elektrycznej tensometrii oporowej opiera się na znanej własności fizycznej drutu metalowego, polegającej na zmianie jego oporu elektrycznego wraz z doznawaną przezeń zmianą długości .

Rozety tensometryczne:

Aby określić stan odkształcenia w pewnym punkcie konstrukcji, należy podać wszystkie współrzędne obiektu, który odkształcenie opisuje, tzn. wszystkie wartości współrzędnych
. Wiadomo że pomiar przy pomocy jednego tylko tensometru takich informacji nie dostarczy. W związku z tym stosuje się układy tensometrów naklejonych w tym samym miejscu lub bardzo bliski siebie zwane rozetami tensometrycznymi.

W praktyce znajduje zastosowanie kilka typów rozet. Najprostsze, lecz możliwe do stosowania tylko, gdy główne kierunki odkształcenia są znane, są rozety prostokątne - utworzone z dwóch tensometrów przylegających do siebie lub skrzyżowanych.

Możemy wyróżnić następujące rodzaje rozet.

• rozety prostokątne,

• rozety typu „delta”,

• rozety zbudowane z czterech tensometrów typu „T - delta”

4. Opracowanie wyników pomiarów.

Wyniki opracowano przy pomocy programu ROZETY.

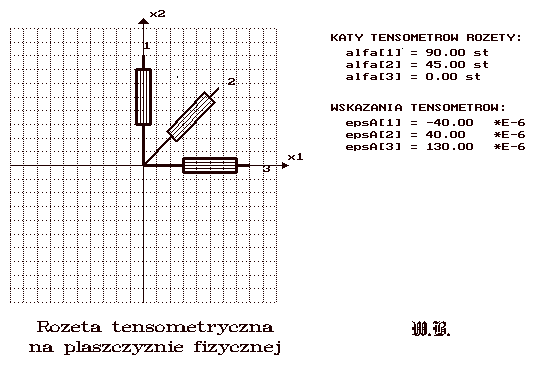
Opracowanie wyników dla rozety prostokątnej:

WYNIKI: DANE:

Odkształcenie - w układzie wsp. {x1,x2}: łł

ł 130.00 -5.00 0.00 ł łł Kąty osi tensometrów

ł ł łł alfa[i] w ukl.{x1,x2}:

eps = ł -5.00 -40.00 0.00 ł*E-6 łł ł 90.0 ł

ł ł łł ł ł

ł 0.00 0.00 -38.57 ł łł alfa= ł 45.0 ł

łł ł ł

Odksztalcenie - w ukladzie wsp. glownych: łł ł 0.0 ł

ł 130.15 0.00 0.00 ł łł

ł ł łł Wydluzenia wzgledne

epsG =ł 0.00 -41.15 0.00 ł*E-6 łł w kierunkach alfa[i]

ł ł łł ł -40.0 ł

ł 0.00 0.00 -38.57 ł łł ł ł

łł epsA= ł 30.0 ł *E-6

Naprezenie - w ukladzie wsp. {x1,x2}: łł ł ł

ł 27.23 -0.81 0.00 ł łł ł 130.0 ł

ł ł łł

sigma= ł -0.81 -0.23 0.00 ł [MPa] łł

ł ł łł

ł 0.00 0.00 -0.00 ł łł M. Younga=210000 [MPa]

łł L. Poissona = 0.3

KAT ODKSZTALCEN /NAPREZEN/ GLOWNYCH łł

fi = -1.68323 st łł

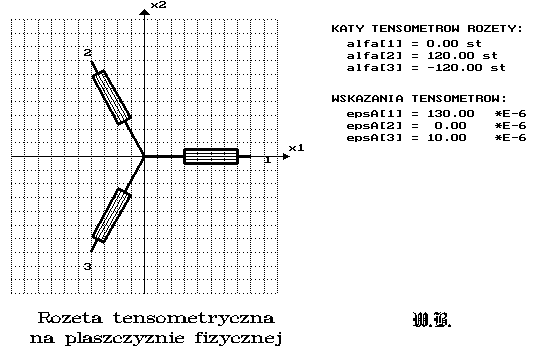
Opracowanie wyników dla rozety równokątnej:

WYNIKI: DANE:

Odksztalcenie - w ukladzie wsp. {x1,x2}: łł

ł 130.00 -5.71 0.00 ł łł Katy osi tensometrow

ł ł łł alfa[i] w ukl.{x1,x2}:

eps = ł -5.71 -36.67 0.00 ł*E-6 łł ł 120.0 ł

ł ł łł ł ł

ł 0.00 0.00 -40.00 ł łł alfa= ł 0.0 ł

łł ł ł

Odksztalcenie - w ukladzie wsp. glownych: łł ł 120.0 ł

ł 130.20 0.00 0.00 ł łł

ł ł łł Wydluzenia wzgledne

epsG =ł 0.00 -36.87 0.00 ł*E-6 łł w kierunkach alfa[i]

ł ł łł ł 10.0 ł

ł 0.00 0.00 -40.00 ł łł ł ł

łł epsA= ł 130.0 ł *E-6

Naprezenie - w ukladzie wsp. {x1,x2}: łł ł ł

ł 27.00 -0.93 0.00 ł łł ł 0.0 ł

ł ł łł

sigma= ł -0.93 0.54 0.00 ł [MPa] łł

ł ł łł

ł 0.00 0.00 -0.00 ł łł M. Younga=210000 [MPa]

łł L. Poissona = 0.3

KAT ODKSZTALCEN /NAPREZEN/ GLOWNYCH łł

fi = -1.98162 st łł

5. Wnioski.

Dzięki zastosowaniu rozet tensometrycznych mogliśmy określić odkształcenia główne oraz znaleźć kąt odkształceń (naprężeń) głównych. Z wyników widać że próbka była rozciągana w kierunkach є₁₁ , a ściskana w pozostałych kierunkach. Główne tensory odkształceń dla obu rozet są do siebie dosyć podobne.

Naprężenie reedukowane według Hubera wynosi

-dla tensora naprężenia dla prostokątnej rozety:

-dla tensora naprężenia dla równokątnej rozety:

---