5a.a) Definicja odwzorowania 
różniczkowalnego w punkcie x0. Definicja pochodnej funkcji F w punkcie x0 oraz różniczki dF(x0)h.
5a.a) Definicja odwzorowania
różniczkowalnego w punkcie x0. Definicja pochodnej funkcji F w punkcie x0 oraz różniczki dF(x0)h.
def. Mówimy, że odwzorowanie f jest różniczkowalne w pkt. X0 , jeśli istnieje odwzorowanie liniowe f `(x0):U x0 
x
takie, że 
gdzie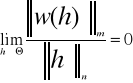 
Odwzorowanie liniowe f `(x0 ) nazywa się pochodną odwzorowania f w pkt. x0 . Wartość odwzorowania f `(x0 ) dla przyrostu h nazywa się różniczką zupełną i piszemy df(x0 ,h).
5a.b) Uzasadnić że funkcja 
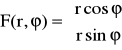
jest różniczkowalna w punkcie x0 = (1,π)
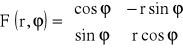
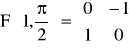
stąd 
F-cja różniczkowalna.