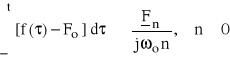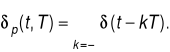Tomasz Madejski

WPROWADZENIE DO SYSTEMÓW TELEKOMONIKACYJNYCH -SEMINARIUM.

Semestr zimowy 2000/2001.

Prowadzący: dr inż. Wojciech J. Krzysztofik.

Zadanie Z1/6.

Wyznaczyć metodą pochodnych współczynniki Fn rozkładu w wykładniczy szereg Fouriera następujących funkcji:

1.Wstęp teoretyczny.

Podstawowym aparatem matematycznym analizy widmowej są szereg i przekształcenie (transformata) Fouriera. Z jego istoty wynika, że każdą funkcję okresową (w tym przypadku sygnał) spełniającą określone warunki (tzw. warunki Dirichleta :

1.posiadający skończoną liczbę punktów nieciągłości w okresie,

2.posiadający skończoną liczbę ekstremów (przedziałami monotoniczny),

3.bezwzględnie całkowalny w okresie) można przedstawić w postaci równoważnego jej szeregu Fouriera w postaci trygonometrycznej lub wykładniczej (zespolonej):

,
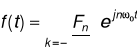
- pulsacja podstawowa

gdzie:

,

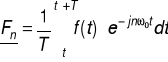
Tak więc istotą przekształcenia Fouriera jest przedstawienie sygnału okresowego w postaci sumy elementarnych drgań harmonicznych.

Własności wykładniczego szeregu Fouriera:

Jeżeli f(t) ↔ F_n oraz g(t) ↔ G_n, wówczas:

1. Liniowość: a f(t) + b g(t) ↔ a F_n + bG_n (jeżeli f(t) i g(t) mają ten sam okres).

2. Przesunięcie w dziedzinie czasu: f(t - t_o) ↔ F_n e^{- j n ω}_o^t_o (liniowa zmiana widma fazowego: ϕ_n = arg F_n - nω_ot_o),

3. Różniczkowanie funkcji czasu: df ^k(t)/dt ^k ↔ (jnω_o)^kF_n n ≠ 0.

4. Zmiana skali czasu: f(at) ↔ F_n, (okres f(at) równy T/a, pulsacja podstawowa równa 2πa/T= aω_o), kształt widma identyczny jak f(t).

Całkowanie funkcji czasu:

Bardzo użyteczną funkcją periodyczną jest periodyczny ciąg impulsów delta Diraca:

Korzystając z własności próbkujących funkcji delta Diraca znajdujemy:

δ_p(t, T) ↔ F_n =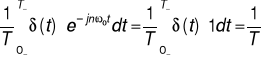


2.Rozwiązanie zadania.

a)

Korzystając z metody pochodnych i wzorów przytoczonych w części teoretycznej obliczamy odpowiednie współczynniki rozwinięcia Fouriera (dla T = p,czyli
=2) :

Jak widać z powyższych rysunków po dwukrotnym zróżniczkowaniu funkcji f(t) otrzymaliśmy ciąg funkcji impulsowych oraz funkcję okresową -f(t).

Możemy teraz ułożyć następujące równanie:




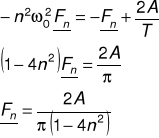
Ostatecznie:




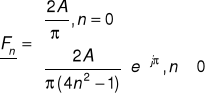
b)

Korzystając z metody pochodnych i wzorów przytoczonych w części teoretycznej obliczamy odpowiednie współczynniki rozwinięcia Fouriera (dla T = 2p,czyli
=1) :




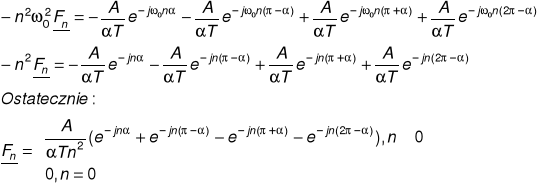
c)

Korzystając z metody pochodnych i wzorów przytoczonych w części teoretycznej obliczamy odpowiednie współczynniki rozwinięcia Fouriera (dla T = 2p,czyli
=1) :




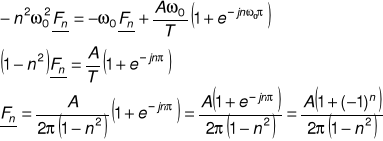
Współczynnik pierwszej harmonicznej musi być policzony z definicji :







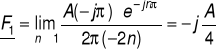
Ostatecznie:




Wnioski:

Analiza widmowa sygnałów należy do podstawowych narzędzi matematycznych we współczesnej elektronice i telekomunikacji, a zwłaszcza w teorii sygnałów. Umożliwia ona przedstawienie każdego sygnału okresowego za pomocą analitycznej funkcji zespolonej w postaci szeregu zwanego szeregiem Fouriera. Dzięki zastosowaniu metody pochodnych można stosunkowo szybko i łatwo wyznaczyć współczynniki Fn skomplikowanych funkcji okresowych.

---