Paweł Czuczwara Semestr zimowy 2000/2001

Nr.94351

WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH

SEMINARIUM

I. Zadanie Z-1 / 1

Rozwinąć w trygonometryczny szereg Fouriera funkcję f(t) przedstawioną na rysunkach

a) , b) , c), w przedziale (0,1).

f(t) f(t) f(t)

A A A

a) b) c)

0 1 t 0 1 t 0 1 t

2. Wprowadzenie

Z analizy matematycznej wynika, że każdą okresową funkcję czasu o okresie T , która w dowolnym przedziale czasu T jest funkcją regularną oraz funkcją o ograniczonej zmienności ,można rozłożyć w trygonometryczny szereg Fouriera o postaci:

f(t) = a₀/2 + ( a_k cos(kω₀t)+ b_ksin(kω₀t)),

gdzie: a₀=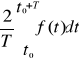
,

a_k =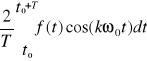
,

b_k=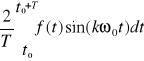
,

oraz ω₀=2π/T, zaś t₀ może być wybrane dowolnie.

Można wprowadzić zespolony współczynnik F_k określony dla dowolnego całkowitego k .

wówczas szereg Fouriera można zapisać w postaci wykładniczego szeregu Fouriera

f(t)=

gdzie F_k =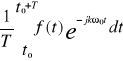
,.

3. Rozwiązanie zadania.

a) Korzystam z definicji obliczając a₀, a_k, b_k :

Funkcję zapisuję jako f(t) = a⋅t ,oczywiście dla t∈ < 0,1 >.

a₀=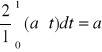

uogólniając wzór dla wszystkich k otrzymujemy .

a_k =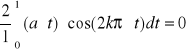
b_k =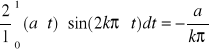

Stąd też otrzymujemy :

I tak dla przykładu dla a=6 i rozwinięciu w szereg k=1..7 o trzymujemy :

wykres :

b) Funkcję zapisuję jako f(t) = a ,oczywiście dla t∈ < 0,1 >.

a₀=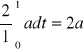

uogólniając wzór dla wszystkich k otrzymujemy .

a_k =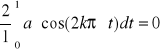
b_k =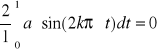

Stąd też otrzymujemy :

c) Funkcję zapisuję jako f(t) = -a⋅t + a ,oczywiście dla t∈ < 0,1 >.

a₀=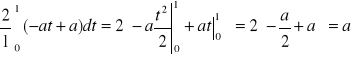

uogólniając wzór dla wszystkich k otrzymujemy .

a_k =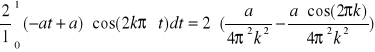

b_k =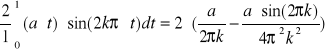

Stąd też otrzymujemy :

I tak dla przykładu dla a=6 i rozwinięciu w szereg k=1..7 o trzymujemy :

wykres :

4. Wnioski .

Jak widać istnieje łatwa metoda wyznaczania współczynników szeregu Fouriera- szczególnie gdy badana funkcja jest matematycznie łatwa do zapisu. Przy pomocy narzędzi obliczeniowych, takich jak kalkulator czy komputer istnieje szybka możliwość wyliczeniowa. W powyższej metodzie korzystałem bezpośrednio z definicji, są oczywiście inne metody opierające się na właściwościach szeregów Fouriera. Większość tych twierdzeń ustala relacje między operacjami wykonywanymi na widmach tych sygnałów w dziedzinie częstotliwości . Operacje w dziedzinie częstotliwości polegają na odpowiednim przekształceniu widma lub widm sygnałów w inne widmo - widmo sygnału otrzymanego jako wynik operacji w dziedzinie czasu.

1

3