Piotr Kozioł 6.10.2000r.
WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
Seminarium sem. zimowy 2000/2001
Zadanie Z1/4
Treść zadania
Rozwinąć funkcję f(t) = 6t w szereg Fouriera w przedziale (0,1) tzn. przedstawić funkcję f(t) przez liniową kombinację funkcji ortogonalnych g(t).
f(t) = { 6t dla 0 < t <1
0 poza przedziałem
Wstęp
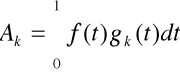
W zadaniu tym mam za zadanie rozłożyć daną funkcję f(t) na sumę funkcji g(t) pomnożonych przez odpowiednie współczynniki szeregu Fouriera. Funkcje g(t) są tutaj bazą. Bardziej znanymi bazami są funkcje Haara i Walscha. Jednak sposób wyznaczania współczynników jest ten sam tzn. należy policzyć całki:
Rozwiązanie
Aby przedstawić funkcję f(t) w postaci:
f(t)=A0g0(t) + A1g1(t) + A2g2(t) +...
muszę wyznaczyć kolejne współczynniki Ak szeregu Fouriera. W tym celu skorzystam ze wzoru:
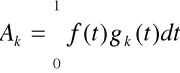
Współczynników tego szeregu jest nieskończenie wiele. Obliczę więc kilka z nich i na tej podstawie ustalę wzór, którym będę mógł obliczyć następne.
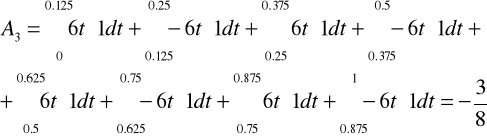
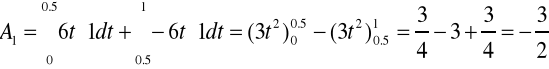
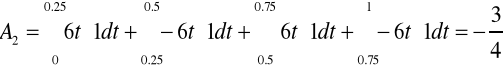
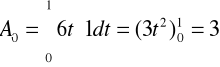
Na podstawie wyliczonych pierwszych czterech współczynników mogę już napisać wzór pozwalający obliczyć dowolny współczynnik.
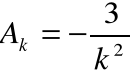
dla k >=1
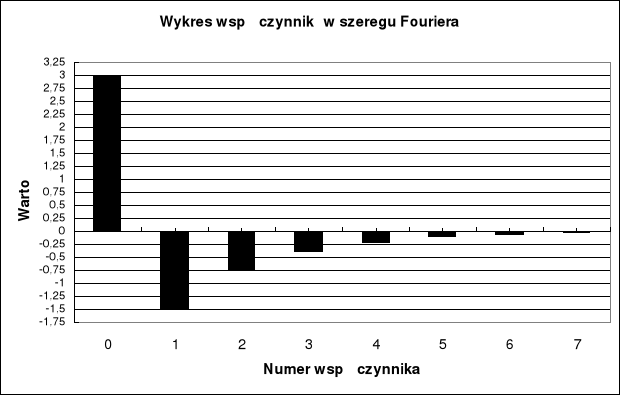
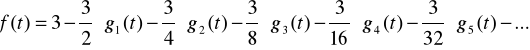
A więc:
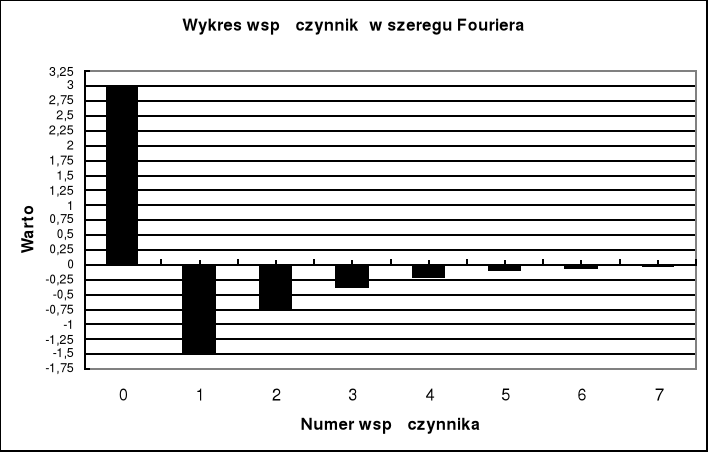
Wnioski
Jak widać postać tej kombinacji liniowej jest bardzo prosta. Współczynnik pierwszy jak można się łatwo domyślić to wartość średnia funkcji f(t) na przedziale (0,1).
3
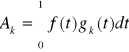
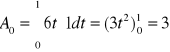
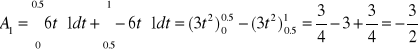
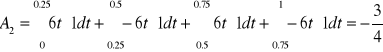
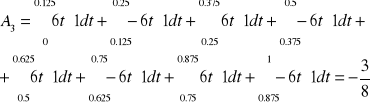
![]()
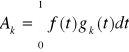
![]()
Wyszukiwarka
Podobne podstrony:
z1 02, SPRAWOZDANIA czyjeś
z1 15, SPRAWOZDANIA czyjeś
z1 07, SPRAWOZDANIA czyjeś
z1 10, SPRAWOZDANIA czyjeś
z5 04, SPRAWOZDANIA czyjeś
Z2 04, SPRAWOZDANIA czyjeś
z1 07a, SPRAWOZDANIA czyjeś
Z1 06, SPRAWOZDANIA czyjeś
Z1 13, SPRAWOZDANIA czyjeś
Z1 01, SPRAWOZDANIA czyjeś
z4 04, SPRAWOZDANIA czyjeś
z1 05, SPRAWOZDANIA czyjeś
z3 04, SPRAWOZDANIA czyjeś
zlotnik jubiler 731[06] z1 04 u
mechanik pojazdow samochodowych 723[04] z1 04 n
lakiernik 714[03] z1 04 n
więcej podobnych podstron