03.11.1999
Rozwiązanie zadania nr.7 z listy pierwszej
Janusz Garbera
88010
Środa, godz. 1315 - 1500 , sala 142, bud. C-4
Prowadzący: dr inż. Wojciech J. Krzysztofik
Do podstawowych własności transformaty Fouriera należą:
Liniowość
af(t)+bg(t) = aFk+bFk
różniczkowalność
f '(t) = jkωoFk
przesunięcie w dziedzinie czasu
f(t-to) = e-jkωotoFk
Wykorzystując te własności można w prosty sposób wyznaczyć transformaty Fouriera sygnałów zadanych w zadaniu.
Rozwiązanie
Jeżeli sygnały mają skończoną energię (tak jak w zadaniu) to możemy użyć metody różniczkowania oraz wyżej wymienionych własności transformaty Fouriera.
F(jϖ)
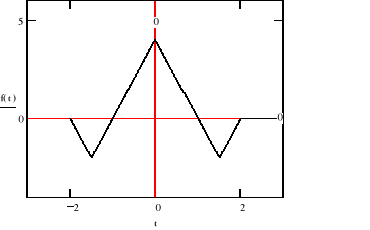
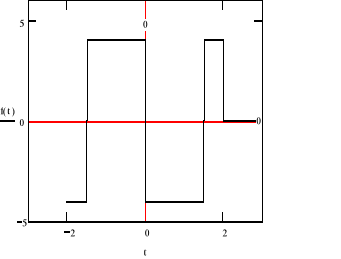
a)
Po zróżniczkowaniu otrzymujemy :
jϖF(jϖ)
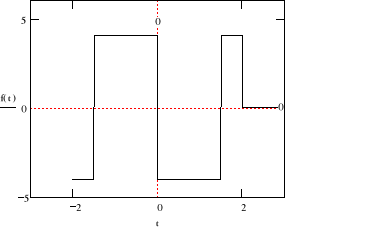
Po kolejnym zróżniczkowaniu otrzymujemy:
-ϖ2F(jϖ)
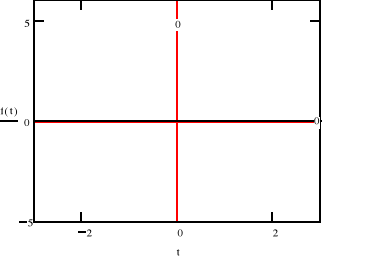
Obliczmy transformatę Fouriera:
![]()
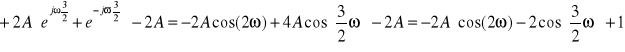
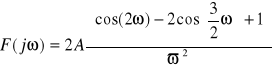
Mamy więc:
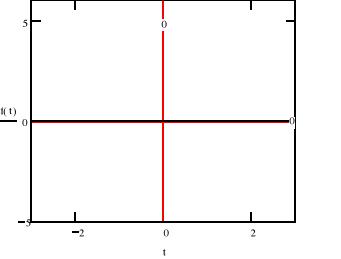
b)
Używając tej samej metody:
F(jϖ)
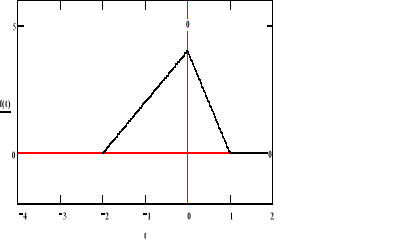
Po zróżniczkowaniu:
jϖF(jϖ)
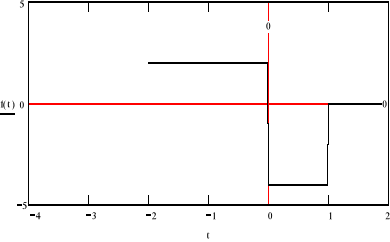
Po kolejnym zróżniczkowaniu:
-ϖ2F(jϖ)
![]()
Obliczmy transformatę Fouriera:
![]()
Stąd:
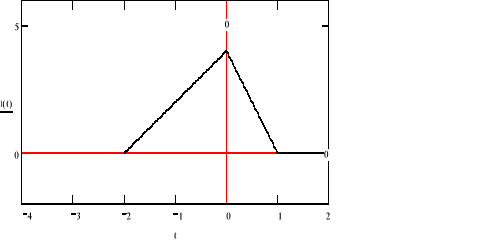
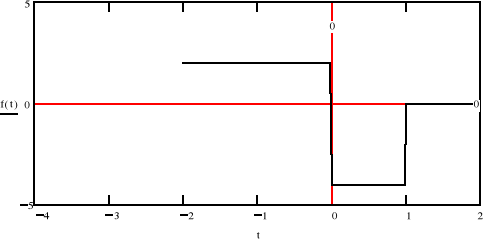
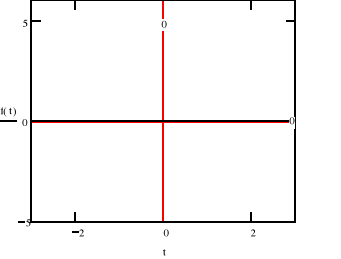
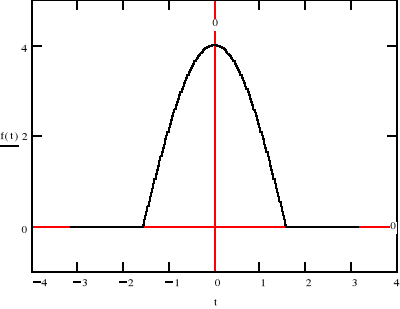
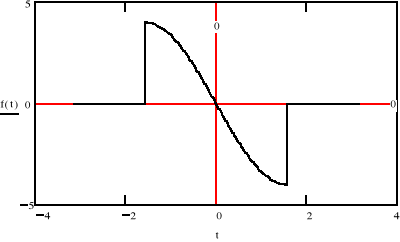
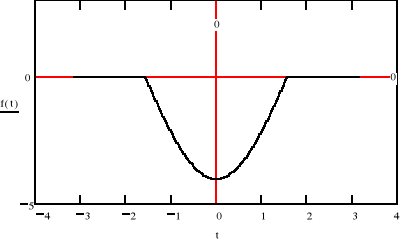
c)
F(jϖ)
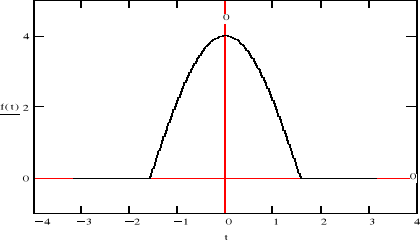
Po zróżniczkowaniu:
jϖF(jϖ)
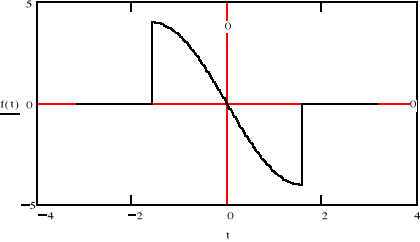
Po ponownym zróżniczkowaniu:
-ϖ2F(jϖ)
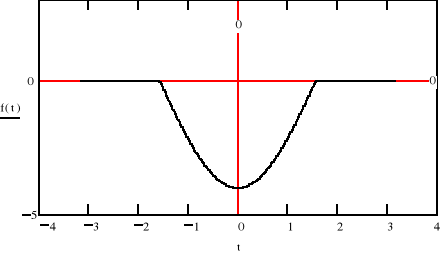
Obliczmy transformatę Fouriera:
![]()
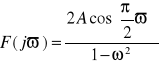
Więc:
Wnioski
Jak widać wykorzystując własności transformaty Fouriera możemy w dość prosty sposób przedstawić dowolny przebieg o skończonej energii w dziedzinie częstotliwości . W podpunkcie c) możemy zaobserwować ciekawą własność .Mimo , że przebieg jest częścią funkcji cos(t) , której widmo składa się tylko z jednego prążka ,nasz przebieg ma ich więcej. Te dalsze składowe zerują przebieg poza przedziałem (-π/2, π/2) .

![]()
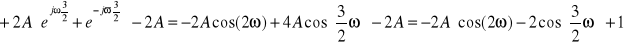
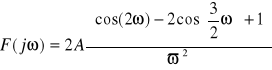
![]()
![]()
![]()
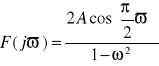
Wyszukiwarka
Podobne podstrony:
z1 02, SPRAWOZDANIA czyjeś
z5 07, SPRAWOZDANIA czyjeś
z1 15, SPRAWOZDANIA czyjeś
z1 10, SPRAWOZDANIA czyjeś
z1 07a, SPRAWOZDANIA czyjeś
z3 07, SPRAWOZDANIA czyjeś
Z1 06, SPRAWOZDANIA czyjeś
Z1 13, SPRAWOZDANIA czyjeś
Z1 01, SPRAWOZDANIA czyjeś
Z1 04, SPRAWOZDANIA czyjeś
z1 05, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
z 1 7 a, SPRAWOZDANIA czyjeś
zegarmistrz 731[05] z1 07 n
więcej podobnych podstron