Piotr Kozioł 26.11.2000r.

WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH

Seminarium sem. zimowy 2000/2001

Zadanie Z4/4

1. Treść zadania

Obliczyć wartość stałej X_A, przy której zachodzi równość mocy szumów kwantyzacji dla sygnałów losowych o różnych gęstościach prawdopodobieństwa. Gęstość prawdopodobieństwa jednego z sygnałów jest funkcją stałą w przedziale <-X_A,X_A> równą 1/2X_A, zaś drugiego opisana zależnością:

dla -B < x < B i B=3*10­⁴

Dla obu sygnałów stosuje się taką samą liczbę przedziałów i charakterystykę kompresji typu μ (μ=100).

2. Wstęp

Szum kwantowania wynika z różnicy pomiędzy sygnałem przed i po operacji kwantowania. Dla kwantowania równomiernego jego moc wynosi

gdzie M - liczba przedziałów.

Moc tą dla sygnałów rzeczywistych (których wartość średnia na ogół jest kilkakrotnie mniejsza od wartości maksymalnej) można zmniejszyć poprzez zastosowanie odpowiedniej kompresji przed kwantowaniem. Kompresja ta sprawi, że przedziały kwantowania będą miały różną szerokość.

Charakterystyka typu μ oznacza, że

gdzie x -znormalizowany sygnał wejściowy

y - znormalizowany sygnał wyjściowy

Wtedy

Wzór na moc szumu w przypadku kwantowania nierównomiernego i dużego M wygląda tak:

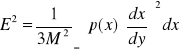
gdzie p(x) - gęstość prawdopodobieństwa

3. Rozwiązanie

Aby obliczyć szukaną stałą policzę moce szumów kwantyzacji dla obu sygnałów (korzystając z podanego wyżej wzoru). Następnie porównam je i z otrzymanego równania wyznaczę stałą X_A.

Ponieważ, obie gęstości są funkcjami parzystymi, więc całkowanie przeprowadzę tylko dla dodatnich wartości.

Moc szumów pierwszego sygnału:

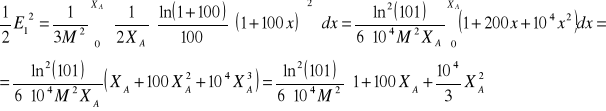
Moc szumów drugiego sygnału:

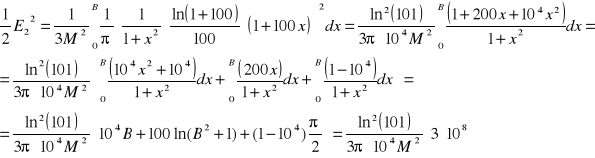
A więc skoro te moce są równe to:

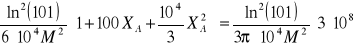
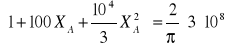
Otrzymałem równanie kwadratowe, które po rozwiązaniu dało mi szukaną wartość

X_A = 239,35

4. Wnioski

Jak widać otrzymana stała jest dużo mniejsza od wielkości B=3*10⁴. Oznacza to, że w przypadku sygnałów o stałej gęstości prawdopodobieństwa nie należy stosować tego typu kompresji.

1

---