Tomasz Madejski
WPROWADZENIE DO SYSTEMÓW TELEKOMONIKACYJNYCH -SEMINARIUM.
Semestr zimowy 2000/2001.
Prowadzący: dr inż. Wojciech J. Krzysztofik.
Zadanie Z4/2.
Sygnał losowy o gęstości prawdopodobieństwa opisanej funkcją Gausa:
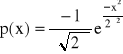
dla -∞ > x < ∞ .
jest podany kompresji z charakterystyką typu A ( A=87.6).
Dla jakiej wartości odchylenia standardowego δ stosunek mocy sygnału do mocy szumów kwantyzacji (P/![]()
) przy idealnym kwantowaniu logarytmicznym będzie taki sam jak przy kwantowaniu równomiernym?
1.Wstęp teoretyczny.
Moc sygnału jest równa:
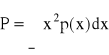
Moc szumów kwantyzacji w przypadku kwantowania równomiernego ( Wszystkie przedziały kwantowania mają jednakową szerokość - Jeśli zakres zmienności sygnału wyjściowego podzielimy na M części to szerokość jednakowych przedziałów kwantowania jest równa 2/M) wynosi:
![]()
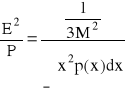
Dla kwantowania równomiernego stosunek mocy szumów kwantyzacji do mocy sygnału:
W przypadku nierównomiernego kwantowania sygnał analogowy poddaje się kompresji,a potem stosuje się kwantowanie równomierne.
Charakterystyka kompresji logarytmicznej typu A ma postać:
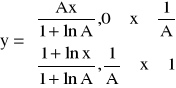
przy czym A przyjmuje się zwykle 87,6.
W przypadku dużej liczby poziomów kwantyzacji moc szumów kwantyzacji wyraża się wzorem:
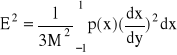
Ostatecznie dla charakterystyki typu A stosunek mocy szumów kwantyzacji do mocy sygnału:
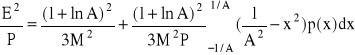
Pierwsza część po prawej stronie wyrażenia przedstawia stosunek szum/sygnał przy idealnym logarytmicznym kwantowaniu. Druga część odpowiada wzrostowi szumu spowodowanego nieidealnym kwantowaniem.
2.Rozwiązanie zadania.
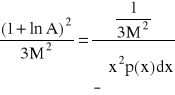
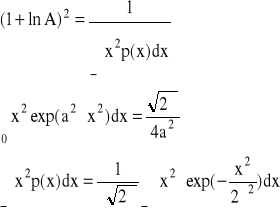
oraz ![]()
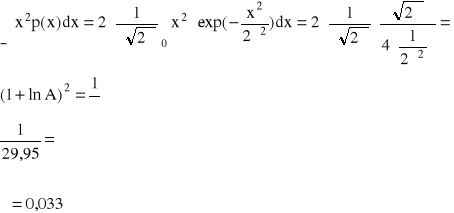
Wnioski:
Kwantowanie równomierne nie jest korzystne.
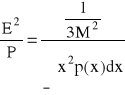
Wyszukiwarka
Podobne podstrony:
z4 06, SPRAWOZDANIA czyjeś
z4 02, SPRAWOZDANIA czyjeś
Z4 03, SPRAWOZDANIA czyjeś
z4 05pg, SPRAWOZDANIA czyjeś
Z4-01, SPRAWOZDANIA czyjeś
z4 04, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
z 1 7 a, SPRAWOZDANIA czyjeś
Zabezpieczenie transformatora za pomocą zespołu automatyki(1), SPRAWOZDANIA czyjeś
w4m, SPRAWOZDANIA czyjeś
Z5 10, SPRAWOZDANIA czyjeś
pomoc, SPRAWOZDANIA czyjeś
siwex, SPRAWOZDANIA czyjeś
MetodyNumeryczne, SPRAWOZDANIA czyjeś
pomoc2, SPRAWOZDANIA czyjeś
więcej podobnych podstron