Funkcja liniowa - zadania przygotowawcze do sprawdzianu
(z rozwiązaniami)
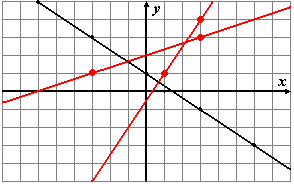
1. Odczytaj z rysunku wzór funkcji, której wykres tam widzisz:
(Przyjmij, że1 jednostka = 1 kratka.) y =... ![]()
(Odp.)
Funkcja ta przyjmuje wartość -1 dla argumentu .....x = 3 (Odp.)
Dla argumentu -3 funkcja osiąga wartość ..... y = 3 (Odp.)
Dorysuj proste:
k1 : ![]()
=> prosta zawiera punkty: (1,1) i (3,4)
k2 : ![]()
=> ![]()
=> (-3,1), (3, 3)
można też od razu z postaci ogólnej wstawić 0 za x i y: (0,2) i (-6,0)
2. (3p) Uzupełnij poniższe zdanie tak, aby opisywało ono funkcję. Podaj dziedzinę i zbiór wartości tej funkcji.
„Każdemu uczniowi przyporządkowano……………………………………………………………………..”
Dziedzina:
Zbiór wartości:
2. ![]()
, ![]()
, ![]()
. Wyznacz równania prostych k i l przechodzących przez C, z których pierwsza jest równoległa do prostej AB, a druga prostopadła do prostej AB.
Rozwiązanie:
![]()
=> ![]()
, ![]()
k: ![]()
, ![]()
=>![]()
=> ![]()
zatem równanie prostej k, to:![]()
(Odp.)
l: ![]()
, ![]()
=>![]()
=> ![]()
zatem równanie prostej l, to: ![]()
(Odp.)
5. Średnia arytmetyczna dwóch liczb dodatnich jest równa dodatniej różnicy tych liczb, natomiast mniejsza liczba po zmniejszeniu o 1 jest cztery razy mniejsza od większej powiększonej o 1. Wyznacz te liczby.
Rozwiązanie: Niech x oznacza większą z tych liczb, a y mniejszą.
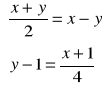
=> (obliczenia na odwrocie! ;-) 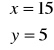
(Odp.)
3. Po Bałtyku pływa kuter, który przecieka z szybkością 10 litrów wody na minutę. W chwili, gdy włączono pompę, w kutrze było 2400 l wody, a przeciek został zatrzymany. Wydajność pompy wynosi 50 litrów na minutę. Przedstaw ilość wody w kutrze (w litrach), jako funkcję czasu t (w minutach) od momentu włączenia pompy. Rozwiązując odpowiednie równanie wyznacz czas, po upływie którego woda zostanie wypompowana. A jak długo trwałoby wypompowanie wody, gdyby nie zatrzymano przecieku?
Rozwiązanie:
Ilość wody pozostającej w kutrze to malejąca funkcja liniowa czasu: ![]()
(Odp.), która argumentowi t (w minutach) przyporządkowuje wartość y (w litrach).
![]()
=> ![]()
=>![]()
(Odp.). Zatem woda zostanie wypompowana po upływie 48 minut. Dziedziną powyższej funkcji jest przedział ![]()
Jeśli woda nadal przecieka, to ![]()
. ![]()
=>![]()
, zatem wypompowanie wody trwałoby godzinę (Odp.)
4. Rozwiąż algebraicznie układ równań:
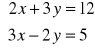
Rozwiązanie: 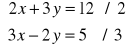
=> 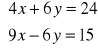
po dodaniu stronami: ![]()
=>![]()
po podstawieniu do pierwszego równania z układu: ![]()
=>![]()
=>![]()
Stąd ![]()
(Odp.)
Wyszukiwarka
Podobne podstrony:
liniowa (3), Matematyka, Liceum
funkca liniowa, Ekonomia- studia, matematyka
liniowa, Matematyka, Liceum
Funkcja liniowa, Matematyka
Układy równań liniowych, Matematyka dla ekonomistów
Funkcja Liniowa, Matematyka- zadania
funkcje liniowe, Matematyka gimnazjum, sprawdziany-Matematyka gimnzjum, klasa3
układ nierówności liniowych matematyka, matura
Zadania z funkcji liniowej z matemaks pl docx
układ nierówności liniowych matematyka, matura
okrag wpisany i opisany, Matematyka, Liceum
Wok Romańska, matematyka liceum
Matematyka nr 1, matematyka, LICEUM, arkusze maturalne, Nowy folder (2)
kwadratowa, Matematyka, Liceum
PL (programowanie liniowe), semestr 8, Matematyka, Teoria i praktyka decyzji ekonomicznych
wykladnicza, Matematyka, Liceum
homograficzna, Matematyka, Liceum
wartość bezwzględna2, Matematyka, Liceum
więcej podobnych podstron