Jeżeli w macierzy A=[a_ij]_m
n zamienimy wiersze na kolumny, a kolumny na wiersze to nazywamy ją macierzą transponowaną i oznaczamy A^T:

A^T=[a_ji]_n
m.

Przykład

A=
, A^T=

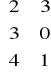
Macierz mającą równą liczbę wierszy i kolumn nazywa się macierzą kwadratową. Jeżeli macierz A jest kwadratowa to można ją zapisać następująco:

A=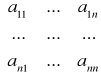
lub krótko A=[a_ij] _n
n.

Elementy a₁₁, a₂₂, … , a_nn tworzą tzw. przekątną główną.

Wyznaczniki

Wyznacznik macierzy A oznaczamy
lub det A.

A=[a₁₁]

B=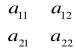
det B=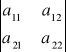

Wyznacznik macierzy [a₁₁], czyli wyznacznik stopnia pierwszego jest równy z definicji liczbie a₁₁. Definiując wyznacznik stopnia n>1 korzysta się z pojęcia wyznacznika stopnia n-1.

Minorem (albo podwyznacznikiem) M_ij macierzy kwadratowej (n>1)

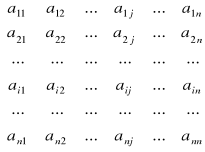
(1)

nazywamy wyznacznik macierzy otrzymanej z powyższej macierzy przez skreślenie i-tego wiersza i j-tej kolumny. Zatem:

M_ij=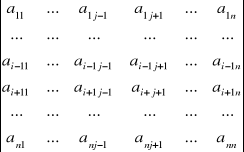

Wyznacznik M_ij jest stopnia n-1.

Wyznacznik stopnia n macierzy (1) nazywamy liczbę

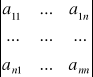
=(-1)¹⁺¹a₁₁M₁₁+(-1)¹⁺²a₁₂M₁₂+…+(-1)¹⁺ⁿa_1nM_1n (2)

Właściwości wyznaczników

1. zamiana wierszy na kolumny i kolumn na wiersze nie zmienia wartości wyznacznika.

2. wyznacznik, w którym wszystkie elementy jednego wiersza (kolumny) są równe zero, jest równy zeru.

3. wyznacznik mnożymy przez stałą, mnożąc elementy jednego wiersza (kolumny) przez stałą.

4. wyznacznik, w którym dwa wiersze (kolumny) są proporcjonalne (lub równe) jest równy zeru.

5. do elementów dowolnego wiersza (kolumny) można dodać elementy innego wiersza (kolumny) pomnożone przez dowolną liczbę. Operacja ta nie zmienia wartości wyznacznika.

---