Przedstawione poniżej zadania są przeznaczone przede wszystkim do samodzielnego rozwiązywania przez studentów. Prowadzący zajęcia ( ćwiczenia i laboratoria) mogą je oczywiście też wykorzystywać, ale mogą je również modyfikować lub rozwiązywać zadania o podobnej skali trudności.

1. Zapisywanie prostych algorytmów w formie schematu blokowego.

1a. Zapisz w postaci słownej algorytm znajdowania pierwiastków równania kwadratowego ax²+bx+c=0, przyjmując założenia : a≠0 oraz b² >4ac.

1b. Jak zmieni się algorytm jeśli zrezygnujemy z drugiego założenia. Tu już lepiej użyć schematu blokowego.

1c. Zrezygnuj również z pierwszego założenia. To już powinien wyjść w pełni uniwersalny algorytm ( radzący sobie z każdym trójmianem).

1d. Wydrukuj dane trzy liczby : A,B i C w kolejności rosnącej.

1e. Uporządkuj dane trzy liczby : A,B i C w kolejności rosnącej. Jaka jest różnica między tymi algorytmami.

1f. Uporządkuj pięć liczb: A,B,C,D i E, tak aby wykonać jak najmniejszą liczę porównań. Ile ich jest ? - jeśli 8 to szukaj dalej.

1g. Narysuj schemat blokowy algorytmu sprawdzającego czy z odcinków o długościach A,B,C można zbudować trójkąt, jeśli tak to jaki :

a) równoboczny, równoramienny czy różnoboczny

b) ostrokątny, prostokątny czy rozwartokątny ?

1h. Czy przyjęcie założenia A ≤ B ≤ C upraszcza algorytm ? Jeśli tak, to może warto go rozbudować o wstępne sortowanie liczb.

1i. Spróbuj opisać algorytm sterowania robotem, który ma zadzwonić z automatu telefonicznego. Przyjmij, że robot rozumie proste polecenia typu: znajdź automat, podejdź, podnieś słuchawkę itp.

2. Schematy blokowe c.d. - algorytmy iteracyjne.

2a. Oblicz sumę cyfr liczby naturalnej K.

2b. Ile cyfr znaczących ma liczba naturalna K ?

2c. Jaka jest najstarsza (pierwsza z lewej) cyfra liczby naturalnej K ?

2d. Czy w zapisie liczby naturalnej K występuje cyfra C ?

2e. Jaka jest największa cyfra liczby naturalnej K ?

2f. Jaka cyfra występuje najczęściej w zapisie liczby naturalnej K ?

2g. Sprawdź czy liczba naturalna K jest liczbą pierwszą.

2h. Znajdź największy wspólny podzielnik liczb naturalnych M i N. Czy założenie M ≤ N upraszcza problem ?

2i. Wykorzystaj algorytm Euklidesa (z obliczaniem reszty z dzielenia) do zadania 2h.

2j. Wykorzystaj algorytm Euklidesa (bez wykorzystywania dzielenia) do zadania 2h.

2k. Oblicz X do potęgi K ( K- liczba naturalna). Postaraj się zminimalizować liczbę mnożeń.

Podpowiedź : przyda się znajomość schematu Hornera, tylko dlaczego Hornera skoro algorytm szybkiego

potęgowania był znany w Indiach już 2200 lat temu ?

2l. Korzystając z podanych poniżej wzorów oblicz przybliżone wartości funkcji. Uwaga: aby uzyskać zadowalającą dokładność należy zsumować wiele elementów szeregu (uwaga na przekroczenie zakresu liczb).

3. Zapisywanie algorytmów w JAVIE.

Wybrane z 1 i 2 algorytmy należy zapisać jako metody uproszczonych ( ograniczonych do definicji pól i metod) klas obiektowych.

4. Pełne definicje klas .

Zdefiniuj klasę Data. Klasa powinna przechowywać w formacie dzień, miesiąc, rok i zawierać konstruktor i podstawowe metody odczytujące poszczególne składowe daty i umożliwiające zmianę daty. Należy również zdefiniować dodatkowe metody określające ( Uwaga data oznacza datę zapisaną w polach obiektu wywołującego, natomiast data1 jest przekazywana jako parametr metody - jako obiekt lub osobne wartości dzień, miesiąc , rok) :

4a. czy data jest wcześniejsza od data1

4b. czy rok daty jest rokiem przestępnym

4c. ile dni jest w miesiącu wskazywanym przez data

4d. czy data jest poprawna

4e. zmień data na dzień późniejszą ( wcześniejszą)

4f. zmień data na późniejszą ( wcześniejszą) o miesiąc

4g. zmień data na późniejszą ( wcześniejszą) o rok

Uwaga: Jaka jest różnica między tymi problemami c, d, e ?

4h. oblicz różnicę między data a data1 przy założeniu, że data >= data1

4i. Możemy określić na jaki dzień tygodnia wypadnie określona data obliczając resztę z dzielenia przez 7 ( jeśli ta reszta wychodzi ujemna należy do niej dodać 7 ) następującego wyrażenia :

2.6m-0.2+d +y+y/4+c/4-2c

gdzie: d - numer dnia miesiąca (1,2...),

m - numer miesiąca w roku (marzec=1,kwiecień=2,... ,grudzień=10,styczeń i luty są traktowane jako

11 i 12 miesiąc poprzedniego roku ),

y - dwie ostatnie cyfry roku,

c - dwie początkowe cyfry roku (stulecie),

x - oznacza cześć całkowita z x.

Uwaga: Zależność jest słuszna dla lat 1582 - 4902.

wydrukuj słownie dzień tygodnia przypadający na określona datę.

Pytanie dodatkowe : jakim dniem zaczyna się tydzień ?

5. Przetwarzanie tablic jednowymiarowych.

5a. Zdefiniuj klasę Tablica. Obiekty tej klasy powinny móc zapamiętać do 100 liczb całkowitych ( oczywiście liczba pamiętanych elementów jest zmienna). Podstawowe metody ( konstruktory, gettery i settery ) każdy może opracować sobie sam. My skupimy się na ciekawszych metodach :

• suma wartości elementów tablicy

• wartość maksymalna w tablicy

• element maksymalny (zauważ różnicę między tym zadaniem a poprzednim)

• czy podana ( jako parametr ) wartość występuje na którejś z k (k<=liczba elementów) początkowych pozycji tablicy

• czy tablica jest różnowartościowa ( porównaj rozwiązanie bezpośrednie i rozwiązanie wykorzystujące poprzednią metodę

• usuń wszystkie wystąpienia podanej (jako parametr ) wartości x, kolejność pozostawionych elementów może ulec zmianie

• wyeliminuj wszystkie powtórzenia elementów tablicy itd. itp.

5b. Zdefiniuj klasę TablicaUporządkowana ( niemalejąco ) , przy zachowaniu założeń z 5a. Skupimy się na metodach , które są wyraźnie inne niż te dla zwykłej tablicy.

• wstaw element o podanej (jako parametr ) wartości

• usuń wskazany przez podanie indeksu element

• usuń wskazany przez podanie wartości element ( jeśli takich jest więcej usuwaj ostatni )

• usuń wszystkie wystąpienia wartości x

• czy podana ( jako parametr ) wartość występuje na którejś z k ( k<= liczba elementów) początkowych pozycji tablicy

• wyeliminuj wszystkie powtórzenia elementów tablicy itd. itp.

5c. Zdefiniuj klasę Hotel . Każdy hotel ma określoną liczbę numerowanych pokoi , ustawianą w momencie tworzenia obiektu. Określony pokój jest wyjęty jeśli jest z nim powiązany obiekt klasy Osoba ( taki jak na wykładzie ). Jedna osoba może wynajmować wiele pokoi. Metody do zaprogramowania :

• czy jest jakiś wolny pokój

• ile jest wolnych pokoi

• wynajmij dowolny z wolnych pokoi podanej (jako parametr ) osobie ( obiekt typu Osoba), wynikiem powinien być numer przydzielonego pokoju

• czy osoba o podanym nazwisku wynajmuje jakiś pokój

• zwolnij wszystkie pokoje wynajmowane przez osobę o podanym nazwisku

6. Przetwarzanie tablic wielowymiarowych.

6a. Zdefiniuj klasę Macierz. Obiekty tej klasy powinny móc zapamiętać tablicę dwuwymiarową ( do 10 wierszy i 30 kolumn) liczb całkowitych. Podstawowe metody ( konstruktory, gettery i settery ) każdy może opracować sobie sam. My skupimy się na ciekawszych metodach :

• suma wartości elementów macierzy

• wartość maksymalna w macierzy

• element maksymalny (wynikiem powinien być obiekt klasy Indeks)

• wiersz o maksymalnej sumie wartości elementów

• czy podana ( jako parametr ) wartość występuje w macierzy

• czy macierz jest różnowartościowa

• transponowanie macierzy

Wskazówki : zacznij od macierzy kwadratowej , a następnie spróbuj z macierzą prostokątną ; pewnie przyda się pomocnicza metoda zamieniająca wskazane elementy macierzy ; wyeliminuj zbędne przepisania ( zamiana to trzy przepisania, a czasami wystarczy jedno)

6b. Zdefiniuj klasę MacierzTab traktując macierz jako jednowymiarową tablicę obiektów typu Tablica ( dla uproszczenia zapisu przyjmij, że mamy uprawnienia do bezpośredniego dostępu do pól obiektów typu Tablica) . Obiekty tej klasy powinny móc zapamiętać tablicę dwuwymiarową ( do 10 wierszy i 30 kolumn) liczb całkowitych. Tym razem zajmiemy się metodami, które można zrealizować prościej wykorzystując metody klasy Tablica:

• suma wartości elementów macierzy

• wartość maksymalna w macierzy

• element maksymalny (wynikiem powinien być obiekt klasy Indeks)

• wiersz o maksymalnej sumie wartości elementów

• czy podana ( jako parametr ) wartość występuje w macierzy

• czy macierz jest różnowartościowa

6c. Zdefiniuj klasę Hotel . Każdy hotel ma określoną liczbę numerowanych pokoi rozmieszczonych na poszczególnych piętrach. Liczba pięter i liczba pokoi na każdym piętrze jest ustawiana w momencie tworzenia obiektu. Pokój jest identyfikowany przez obiekt klasy NumerPokoju ( o polach pietro i pokoj ) . Określony pokój jest wyjęty jeśli jest z nim powiązany obiekt klasy Osoba ( taki jak na wykładzie ). Jedna osoba może wynajmować wiele pokoi. Metody do zaprogramowania :

• czy jest jakiś wolny pokój

• ile jest wolnych pokoi

• wynajmij dowolny z wolnych pokoi podanej (jako parametr ) osobie ( obiekt typu Osoba), wynikiem powinien być numer przydzielonego pokoju

• czy mogę wynająć k sąsiednich pokoi ( wynikiem powinien być numer pierwszego pokoju lub null jeśli to niemożliwe)

• czy osoba o podanym nazwisku wynajmuje jakiś pokój

• które pokoje wynajmuje osoba o podanym nazwisku ( wynikiem powinna być tablica numerów pokoi lub null)

• zwolnij wszystkie pokoje wynajmowane przez osobę o podanym nazwisku itp. itd.

7. Definiowanie hierarchii klas - wykorzystanie dziedziczenia.

7a. Zdefiniuj zestaw klas umożliwiający prowadzenie prostej ewidencji płac w Firmie (nie należy się przejmować tym, że przedstawione poniżej założenia są mocno uproszczone a tym samym mało realistyczne ).

Założenia :

• Firma może zatrudniać maksymalnie 100 Pracowników ( do ich zapisania należy użyć jednej tablicy - kolejność zapisu nie ma żadnego znaczenia)

• każdy Pracownik jest jednoznacznie identyfikowany przez nazwisko ( nazwisko jest pełnym identyfikatorem więc nie może być dwóch Pracowników o tym samym nazwisku )

• każdy Pracownik jest zatrudniony na określoną część etatu ( np. 0.5, 1.0 lub 1.25)

• są dwie grupy Pracowników : Urzędnicy i Robotnicy

• na płacę Urzędnika składa się płaca podstawowa ( podana dla całego etatu ) plus określony indywidualnie % premii

• płacę Robotnika oblicza się uwzględniając liczbę przepracowanych godzin i stawkę godzinową; za nadgodziny czyli godziny przepracowane ponad LIMIT ( podawany dla całego etatu i wspólny dla wszystkich Robotników ) należy się 50% dodatku

Żeby nie marnować czasu przyjmij, że podstawowe metody ( konstruktory, gettery i settery) są już zdefiniowane i możemy się skupić na ciekawszych metodach, np. :

• obliczenie wypłaty Pracownika

• znajdź Pracownika o podanym nazwisku ( wynikiem powinna być referencja do obiektu )

• czy Pracownik jest Urzędnikiem ( Robotnikiem)

• przyjmij nowego Urzędnika ( Robotnika ) - dane to nazwisko i na jaką część etatu zatrudniamy

• zwolnij pracownika o podanym nazwisku

• ilu jest zatrudnionych Urzędników ( Robotników )

• jaka jest suma wypłat wszystkich Urzędników ( Robotników)

• wydruk listy płac itp. itd.

7b. Co i jak należy zmienić aby uwzględnić wymaganie, że tablica Pracowników powinna być uporządkowana według nazwisk Pracowników ? Wprowadź odpowiednie zmiany.

8. Praca z kolekcjami obiektów.

8a. Zrealizuj zadanie 7a wykorzystując zbiór nieuporządkowany ( HashSet)

8b. Zrealizuj 7a wykorzystując listę ( ArrayList)

8c. Zrealizuj 7a wykorzystując odwzorowanie ( HashMap)

8d. Jaki rodzaj kolekcji będzie najlepszy do realizacji zadania 7b ?

9. Standardowe wejście i wyjście.

9a. Przyjmując jako punkt wyjścia macierz z zadania 6a. zaimplementuj metody : wczytującą macierz ( podajemy liczbę wierszy i liczbę kolumn oraz elementy macierzy - każdy wiersz macierzy w osobnym wierszu) i drukującą macierz ( macierz powinna wyglądać porządnie, kolumny nie powinny się wyginać; dla uproszczenia przyjmij że wiersz macierzy mieści się w wierszu wydruku). Zadanie należy zrealizować dla elementów typu : int, double,String.

9b. Zmodyfikuj klasy z zadania 7 tak aby było możliwe :

• wprowadzanie danych pracownika przy przyjmowaniu nowego pracownika ( chyba najprościej zmodyfikować odpowiednie konstruktory)

• drukowanie listy płac ( numer kolejny, nazwisko pracownika, urzędnik/robotnik, etat i wypłata)

10. Przetwarzanie plików.

10a. Co i jak trzeba zmienić w rozwiązaniach zadań z punktu 9,aby możliwe było wczytywanie/wydruk z/do pliku tekstowego .

10b. Dla zadania 7 zaimplementuj metody umożliwiające przechowywanie danych między uruchomieniami programu ( odpowiedniki save i restore ).

10c. W pliku o danej nazwie znajduje się pewien tekst. Ile jest wierszy tekstu? Z ilu znaków składa się ten tekst ? Ile jest w nim „czarnych znaków” ? Jaką długość ma najdłuższy wiersz ? Usuń z niego wszystkie wiersze zaczynające się ciągiem „//” . Wyświetl tekst na ekranie pomijając zbędne odstępy między słowami itp.

10d. W pliku binarnym umieszczono ciąg liczb rzeczywistych. Napisz program wczytujący ten ciąg liczb i obliczający wartość średnią i odchylenie średniokwadratowe (sigma) jego elementów . Czy można to zrobić odczytując dane ze zbioru tylko raz ? UWAGA: plik może mieć tak dużo wartości ,że nie zmieszczą się one w tablicy.

Xsr= sigma=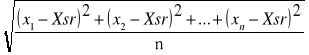

11. Wykrywanie błędów - obsługa wyjątków, wykorzystanie asercji.

Przeanalizuj rozwiązania zadań rozwiązywanych na wcześniejszych zajęciach pod kątem możliwości (i sensowności ) wykrywania i wprowadzenia obsługi sytuacji błędnych. Uzupełnij definicje klas o zgłaszanie nowych wyjątków, ich przechwytywanie i obsługę oraz wstaw odpowiednie asercje.

12. Rekurencja.

12a. Zapisz rekurencyjne wersje znajdowania NWP.

12b. Szybkie potęgowanie.

12c. Liczby Fibbonacciego zdefiniowane są następująco :

Jest to definicja rekurencyjna. Zapisz odpowiednią funkcję. Czy można zmniejszyć liczbę wykonywanych dodawań ? (Przy okazji kto wie jaki jest sens tych liczb ?)

Uwaga : Liczby te można również obliczyć ze wzoru :

(Niewiarygodne ale dla każdego k wynik jest liczbą całkowitą ). Zazwyczaj dla dużych k upraszcza się ten wzór biorąc tylko jego pierwszy człon. Porównaj otrzymane wyniki dla różnych k.

13e. Funkcja Ackermana A(m ,n) (dla m ,n >=0) określona jest zależnością

 n+1 jeśli m=0

A(m ,n) =  A(m-1,1) jeśli m<>0 i n=0

 A(m-1,A(m,n-1)) jeśli n>0 i m>0

Napisz procedurę obliczająca. Ciekawe czy jest to funkcja wolno czy szybko rosnąca ?

12d. Doskonałym przykładem zadania, które bardzo trudno jest rozwiązać bez wykorzystania rekurencji, jest problem znany jako Wieże Hanoi. Napisz program drukujący ciąg przełożeń N krążków prowadzący do rozwiązania.

12e. * Wbrew temu co napisano wyżej rozwiązanie iteracyjne wcale nie jest takie trudne, kto je znajdzie ?

Itbbnt

jr

3

---