Metody i algorytmy sterowania cyfrowego laboratorium
Wykonał:	Temat:	Ocena:
Michał Góra Nr i. 170799	Filtry SOI i NOI

1. Wstęp teoretyczny:

Filtry SOI - filtry nierekursywne o skończonej odpowiedzi impulsowej. Są to filtry w strukturze których nie występuje pętla sprzężenia zwrotnego, każda próbka odpowiedzi nie zależy od poprzednich a jedynie od próbek wymuszenia. W rezultacie odpowiedź impulsowa dowolnego filtru SOI ma zawsze skończoną liczbę próbek. Układy te są zawsze stabilne i charakteryzują się liniowymi charakterystykami fazowymi.

Filtry NOI - filtry rekursywne o nieskończonej odpowiedzi impulsowej. Są to filtry w strukturze których występuje pętla sprzężenia zwrotnego, każda próbka odpowiedzi zależy od poprzednich .W rezultacie odpowiedź impulsowa dowolnego filtru rekursywnego może mieć nieskończoną liczbę próbek. Filtry te charakteryzują się lepszymi charakterystykami amplitudowymi przy niższych rzędzie filtru niż filtry SOI.

Filtry dzielimy na dolnoprzepustowe, czyli takie które przepuszczają niskie częstotliwości, a tłumią wysokie, oraz górnoprzepustowe, które przepuszczają częstotliwości wysokie, a niskie są przez nie tłumione:

2. Filtr górnoprzepustowy o strukturze NOI:

Filtr Butterworth'a II-go rzędu o transmitancji:

Aby przejść na transmitancję dyskretną korzystamy z przekształcenia biliniowego dla filtru górnoprzepustowego:

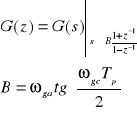
Wyliczenie ω_ga:

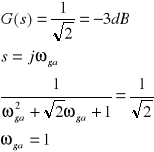
Wyliczenie przekształcenia biliniowego dla filtru górnoprzepustowego:

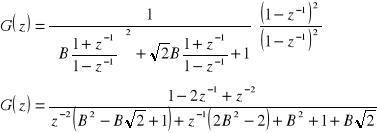
Ścieżka komend w Matlabie:

wga=1;

fgc=245;

wgc=2*pi*fgc;

fp=2300;

tp=1/fp;

B=wga*tan(wgc*tp/2);

L=[1 -2 1];

M=[B^2+B*sqrt(2)+1,2*B^2-2,B^2-B*sqrt(2)+1];

[H,F]=freqz(L,M,512,fp);

subplot(2,2,1),plot(F,abs(H))

title('Odpowiedz czestotliwosciowa filtru')

P=angle(H)*180/pi;

subplot(2,2,2),plot(F,P)

title('Charakterystyka fazowa filtru')

subplot(2,2,3),phasedelay(L,M,512,fp);

title('Opoznienie fazy')

[O,ts]=stepz(L,M);

subplot(2,2,4),plot(ts,O)

title('Odpowiedz na skok jednostkowy')

Wykresy:

3. Filtr górnoprzepustowy o strukturze SOI:

Ilość próbek zależy od częstotliwości próbkowania f p i można ją wyliczyć ze wzoru:

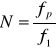
,gdzie

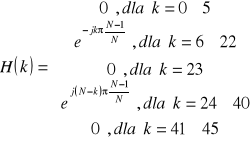
Ścieżka komend w Matlabie:

fgc=275;

fp=2300;

N=46;

H=[zeros(1,6),exp(-j*(6:22)*pi*(N-1)/N),zeros(1,1),exp(j*(N-(24:40))*pi*(N-1)/N),zeros(1,5)];

subplot(2,1,1),stem(0:45,abs(H))

title('wykres dyskretny filtru')

h=ifft(H);

subplot(2,1,2),impz(h,1)

title('odpowiedz impulsowa filtru')

figure(2)

L=h;

M=1;

[H,F]=freqz(L,M,512,fp);

subplot(2,2,1),plot(F,abs(H))

title('Charakterystyka widmowa')

P=angle(H)*180/pi;

subplot(2,2,2),plot(F,P)

title('Charakterystyka czestotliwosciowa')

subplot(2,2,3),phasedelay(L,M,512,fp);

title('opoznienie fazy')

[O,ts]=stepz(L,M);

subplot(2,2,4),plot(ts,O)

title('odpowiedz na skok')

figure(3)

L1=h.*hamming(N)'; %hamming lub hanning lub blackman

M=1;

[H,F]=freqz(L1,M,512,fp);

subplot(2,2,1),plot(F,abs(H))

title('Charakterystyka widmowa')

P=angle(H)*180/pi;

subplot(2,2,2),plot(F,P)

title('Charakterystyka czestotliwosciowa')

subplot(2,2,3),phasedelay(L1,M,512,fp);

title('opoznienie fazy')

[O,ts]=stepz(L1,M);

subplot(2,2,4),plot(ts,O)

title('odpowiedz na skok')

Wykresy:

Charakterystyki wygładzone oknem hamminga:

---