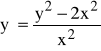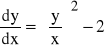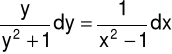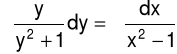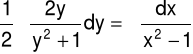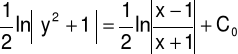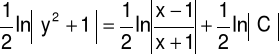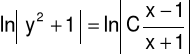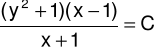Równania różniczkowe zwyczajne rzędu I-go
jednorodne typu: ![]()
Przykład 1
|
(1) |
Rozwiązanie:
|
(2) |
Podstawienie:
|
(3) |
Dzielimy obie strony równania (3) przez iloczyn (x2-1)(y2+1):
|
(4) |
Całkujemy obie strony równania (4), w którym zmienne x oraz y zostały rozdzielone:
|
(5) |
Całkę lewej strony równania (5) mnożymy przez ½, a jej funkcję podcałkową przez 2:
|
(6) |
Wykorzystujemy do lewej strony równania (6) własność 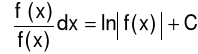
, a do prawej 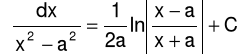
:
|
(7) |
Modyfikujemy stałą C0 w równaniu (7):
|
(8) |
Obie strony równania (8) mnożymy przez 2 i wykorzystujemy do prawej strony własność (a,b>0) ⇒ ( lna + lnb = ln(ab) ) :
|
(9) |
Korzystamy z twierdzenia o równości logarytmów, tzn.
(a,b>0 ∧ lna=lnb) ⇔ (a=b) i z własności bezwzględnej wartości ![]()
:
|
(10) |
Mnożymy obie strony równania (10) przez ![]()
i otrzymujemy całkę ogólną równania różniczkowego (1) w następującej postaci:
|
CORR. |
(11) |
Wyszukiwarka
Podobne podstrony:
Sciaga Rownanie rozniczkowe liniowe pierwszego rzedu
Zestaw 4-Równania liniowe pierwszego rzedu
Zestaw 4 Równania liniowe pierwszego rzedu
05 Rozdział 04 Ogólne równanie uwikłane pierwszego rzędu
05 Rozdział 04 Ogólne równanie uwikłane pierwszego rzędu
Człon inercyjny pierwszego rzędu
Fizyka Matematyczna Wykłady
I 1 2 Chemia fizyka matematyka w kuchni i w lazience konspekt projektu
Pierwszy dzień wakacji, Matematyka, sprawdziany kompetencji po kl VI
Fizyka Matematyczna - Ćwiczenia, Studia Fizyka Techniczna
Fiz teoria prawa fizyczne, Matura, fizyka, matematyka
Konspekt; liczby pierwsze i złożone, Metodyka, Matematyka-konspekty
Pierwszy kosmiczny turysta, Matematyka, sprawdziany kompetencji po kl VI
Program Moje pierwsze 123 zabawy matematyczne - Gruszczyk - Kolczyńska
własności dynamiczne przetworników pierwszego rzędu 2, Mechatronika AGH IMIR, rok 2, sprawozdania, m
Ćw2, Ćw2, Człon inercyjny pierwszego rzędu
więcej podobnych podstron