OBLICZENIA GEODEZYJNE

+x

d P Zależność: α_PA=α_AP+180º

układ geodezyjny lub:

α α_PA=α_AP+200^g

-y 0 +y Kąty kierunkowe można również obliczać za

pomocą tzw. czwartaków. Czwartak jakiegoś

kierunku jest to kąt ostry jaki tworzy dany

kierunek z osią x.

-x

+x IV +x I

P α_PA P

P

α_AP

A A φ φ A

+y φ A +y

A φ

P P

III II

Kąt kierunkowy α, liczony jest od dodatniego kierunku osi x (w prawo) do kierunku danego.

Wartość α= 0º : 360º

0^g : 400^g

Zależności pomiędzy czwartakami φ, a kątami kierunkowymi α
Ćwiartka	Znaki		αAP	Oznaczenie
		Δy			Δx
I	+	+	φ	NO
II	+	-	180º - φ	SO
III	-	-	180º + φ	SW
IV	-	+	360º - φ	NW

OBLICZENIA GEODEZYJNE mają często miejsce w czasie wykonywania pomiarów geodezyjnych (np.: pomiary sytuacyjne, pomiary ciągów poligonowych, ciągów sytuacyjnych i ciągów poligonowych).

1. OBLICZANIE DŁUGOŚCI ODCINKA d_PK:

+x

Dane:

K(x_K,y_K) Punkt początkowy P(x_P,y_P)

Δx_PK -d- Punkt końcowy K(x_K,y_K)

P(x_P,y_P) Obliczenia:

Obliczamy przyrosty współrzędnych

Δy_PK +y Δx_PK = x_K - x_P

Δy_PK = y_K - x_P

RYSOWAĆ W SKALI I WE WŁAŚCIWEJ ĆWIARTCE!!!

2. OBLICZANIE AZYMUTU KIERUNKU PRZECHODZĄCEGO PRZEZ DWA PUNKTY O ZNANYCH WSPÓŁRZĘDNYCH:

Azymut - kąt zawarty między kierunkiem północy a danym kierunkiem.

W zadaniu tym należy wyraźnie określić czy będzie to azymut kierunku biegnącego z punktu P do K czy też odwrotnie (α_PK lub α_KP)

+x

α_KP np. obliczamy α_PK:

K Kolejność obliczeń:

α_PK 1) obliczenie przyrostów Δy i Δx

2) obliczenie

P 3) wyznaczenie kąta φ z tablic (czwartak)

4) uwzględnienie znaków przyrostów

+y 5) obliczenie azymutu α

6) obliczenie kontrolne:

Przykład: Obliczyć azymut kierunku wychodzącego z punktu nr 37 w współrzędnych: x₃₇=368,52m i y₃₇=516,26m i przechodzącego przez punkt nr 36 o współrzędnych: x₃₆=246,56m i y₃₆=179,80m.

+x

516,26 37

czwartak: φ=70,07543531 - tyle stopni

0, 07543531x60=4,52611845 - tyle minut

0,52611845x60=31,567107 - tyle sekund

179,80 36 φ=70º04'31”

246,56 368,52 +y azymut: α_37-36=180º+70º04'31”= 250º04'31”

3. OBLICZANIE WSPÓŁRZĘDNYCH PUNKTU LEŻĄCEGO NA PROSTEJ:

+x

Dane:

B(x_B,y_B) A(x_A,y_A), B(x_B,y_B), l_A-B, l_A-P

l_A-B (z bezpośrednich pomiarów w terenie)

l_A-P P(x_P,y_P) Δx_A-B Obliczenia: P(x_P,y_P)

Δx_A-P

Δy_A-P Na podstawie twierdzenia Talesa:

A(x_A,y_A)

+y y_P=y_A+Δy_A-P=y_A+
Δy_A-B

x_P=x_A+Δx_A-P=x_A+
Δx_A-B

Obliczenie kontrolne: obliczamy l_A-B ze współrzędnych punktów A i B oraz l_A-B po obliczeniu współrzędnych punktu P:x_p,y_p.

Przykład: Obliczyć współrzędne punktu pomierzonego na prostej:

+x

• α_2-1 Dane: X Y

φ -a- Pkt. 1 (575,88m ; 381,48m)

dx Pkt. 2 (659,47m ; 312,51m)

dy P a=75,66m

1

+y Obliczenia: P(x_P,y_P)

1. Obliczam czwartak i azymut:

ćwiartka II → α_2-1=200^g - φ=156^g09^c34^cc

2. Obliczam przyrost współrzędnych:

dx=a∙cosα_2-1=-a∙cosφ=-75,66∙0,771448=-58,37m

dy=a∙sinα_2-1=a∙sinφ=75,66∙0,636293=48,14m

3. Obliczam współrzędne punktu P:

x_P=x₂+dx=659,47-58,37=601,10m

y_P=y₂+dy=312,51+48,14=360,65m

4. Obliczenia kontrolne:

L_2-P=

4. OBLICZANIE KĄTA POMIĘDZY DOWOLNYMI BOKAMI NA PODSTAWIE WSPÓŁRZĘDNYCH:

N

α_CL L Dane:

Współrzędne punktów L, C i P

α_CP P

Obliczenia: kąt β

β

C Zadanie polega na obliczeniu kąta β jako różnicy argumentów boków

CL i CP (wzorem Hausbrandta)

Przykład:

Dane: L(x=345,15 ; y=620,30) ; P(x=300,75 ; y=640,60) ; C(x=260,15 ; y=560,10).

Δx_CL=+85,00

Δy_CL=+60,20

Δx_CP=+40,60

Δy_CP=+80,50

27,92853315 - tyle stopni

0,92853315x60=55,71198876 - tyle minut

0,71198876x60=42,7193256 - tyle sekund

β=27º55'43”

5. WYZNACZENIE POŁOŻENIA PUNKTU METODĄ WCIĘCIA W PRZÓD:

N N

C

Dane:

-a- Współrzędne punktów A i b oraz kąty α i β z

β_BC -b- bezpośrednich pomiarów w terenie

Obliczenia: Współrzędne punktu C

β β_BA α

B A

α_AB α_AC

1. obliczenie długości boku a

2. obliczenie azymutu boku BC

3. obliczenie współrzędnych punktu C

x_C=x_B+Δx_BC

y_C=y_B+Δy_BC

4. obliczenie współrzędnych punktu C wychodząc z punktu A (obliczenie kontrolne)

5. wyznaczenie ostatecznej wartości współrzędnej punktu C, jako średniej arytmetycznej z obu obliczeń:

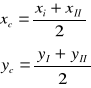
Obliczenia szczegółowe:

Z trójkąta ABC otrzymujemy:

gdzie:

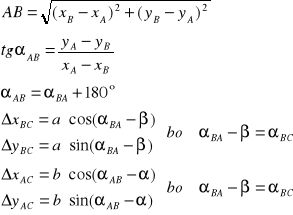
Następnie obliczamy dwukrotnie współrzędne punktu C (z punktu A i B) i obliczamy wartości średnie.

OSTATECZNIE:

z punktu B: z punktu A:

x_C'=x_B+Δx_BC x_C”=x_A+Δx_AC

y_C'=y_B+Δy_BC y_C”=y_A+Δy_AC

6. OBLICZENIE WSPÓŁRZĘDNYCH PUNKTU POMIERZONEGO NA PROSTOPADŁEJ:

+x

B Dane:

Q α_Q-P A(x_A,y_A)

^. -a- B(x_B,y_B)

h α_A-B­ a, h (z bezpośrednich pomiarów w terenie)

A
AQP=90º

P

Obliczenia: P(x_P,y_P)

+y

Przykład:

Dane: A(712,00m 416,38m)

B(936,20m 368,00m)

a=120,50m h=21,50m

1. Obliczam czwartak i azymut:

IV ćwiartka: α_A-B=360º-φ=347,822892º

2. Obliczam przyrost współrzędnych z A do Q:

sinα_A-B=-0,210934 cosα_A-B=0,977500

dy_A-Q=120,50 sinα_A-B=-25,42m

dx_A-Q=120,50 cosα_A-B=117,76m

3. Obliczam współrzędne punktu Q:

x_Q=x_A+dx_A-Q=829,79m y_Q=y_A+dy_A-Q=390,96m

4. Obliczam azymut α_Q-P:

α_Q-P=α_A-B - 90º=257,822892 III ćwiartka

5. Obliczam przyrost współrzędnych z Q do P:

sinα_Q-P=sin(α_A-B - 90º)=-cosα_A-B

cosα_Q-P=cos(α_A-B - 90º)=sinα_A-B

dy_Q-P=21,50(-cosα_A-B)=-21,02m

dx_Q-P=21,50(-sinα_A-B)=-4,54m

6. Obliczam współrzędne punktu P:

X_P=x_Q+dx_Q-P=825,25m y_P=y_Q+dy_Q-P=369,94m

7. Obliczenia kontrolne:

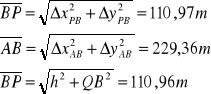
7. OBLICZANIE POWIERZCHNI:

Obliczanie powierzchni pomierzonej figury w terenie lub na mapie można wykonać:

1. metodą analityczną - na podstawie elementów pomierzonych w terenie (długość, kąty). Jest to metoda najdokładniejsza

2. metodą graficzną - na podstawie elementów pomierzonych na mapie

3. metodą mechaniczną - na podstawie mapy, za pomocą przyrządów zwanych planimetrami

4. metodą kombinowaną - na podstawie elementów pomierzonych częściowo w terenie, częściowo graficznie na mapie.

Ad. 1)

Obowiązują tu rozmaite wzory (np. dla trójkąta dowolnego)

A

α

-b- -c-

h_c h_b

C γ h_a β B

-a-

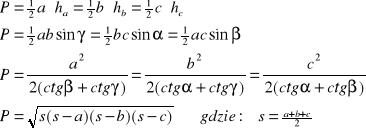
PAMIĘTAĆ O TYM, JAKĄ WARTOŚĆ WYLICZAMY: P CZY 2P!!!

+x 3

1 Metoda współrzędnych biegunowych

r₁ n=1,2,3... wierzchołków wieloboków

r₂

φ₁ φ₂ φ₃ r₃ 2P=r₁r₂sin(φ₂ - φ₁)+r₂r₃sin(φ₃ - φ₂) - r­₁r₃sin(φ₃ - φ₁)

+y

kontrola obliczenia różnic

Można wymienić też wiele innych wzorów!!!

• Obliczanie powierzchni dowolnego wieloboku ze współrzędnych:

+x

1(x₁,y₁) kierunek obliczania

5(x₅,y₅)

2(x₂,y₂)

4(x₄,y₄) 3(x₃,y₃)

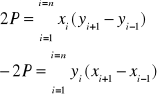
Są to wzory Gaussa na obliczanie powierzchni dowolnego wieloboku.

Wzory kontrolne:

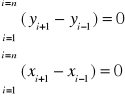
Wskazówka: Wielobok należy opisać liczbami zgodnie z ruchem wskazówek zegara.

Przykład:

Punkt	współrzędne w metrach		a=yi+1-yi-1	b=xi+1-xi-1	xi∙ai	yi∙bi
		yi­					xi
(4)	(+36,21)	(-25,16)
1	+15,42	+2,31	+5,11	+48,81	+11,80	+752,65
2	+41,32	+23,65	+57,21	+1,97	+1353,02	+84,40
3	+72,63	+4,28	-5,11	-48,81	-21,87	-3545,07
4	+36,21	-25,16	+57,21	-1,97	+1439,40	-71,33
(1)	(+15,42)	(+2,31)	Σ=0	Σ=0

+x 2

20

10

1 3

10 20 30 40 50 60 70 +y

-10

-20 4

AD. 2)

Przy obliczaniu powierzchni na mapie metodą graficzną (jak i mechaniczną) należy uwzględnić skurcz papieru (mapy).

Wielkość skurczu określa się na podstawie bezpośredniego pomiaru tzw. ramy sekcyjnej (jej wymiarów) i porównanie wyników pomiaru z wymiarami, jakie rama sekcyjna powinna mieć.

-a-

rama OZNACZENIA:

sekcyjna a,b - wymiary jakie powinna mieć rama sekcyjna

-b- a',b' - wymiary ramy pomierzone na mapie

Skurcz w kierunku boku a wynosi:

Skurcz w kierunku boku b wynosi:

Skurcz powierzchniowy:

ΔP%=p%+q%

Skurcz liniowy w dowolnym kierunku:

K%=P%sin²α +q%cos²α

Pomierzoną na mapie długość odcinka l' należy zmienić o pewną wartość, aby otrzymać odcinek l poprawiony o skurcz papieru:

Oznaczając przez P' powierzchnię obliczoną na mapie, a przez P powierzchnię poprawioną ze względu na skurcz mapy otrzymamy:

Metody graficzne należą do mniej dokładnych sposobów obliczania powierzchni. Obarczone są:

• błędami pomiaru

• 
  błędami grafiki wykreślonej mapy

• błędami odczytów na podziałce

• błędami określenia skurczu papieru

Ad. 3)

Obliczanie powierzchni metodą mechaniczną wykonuje się za pomocą planimetru. Najczęściej stosowany jest planimetr biegunowy. Części składowe planimetru:

- ramie biegunowe i wodzące

- biegun

- wodzik

- kółko kompensacyjne

- licznik (odczyty z licznika są zawsze w postaci liczby czterocyfrowej: I z tarczy poziomej, II i III

z bębna, IV z noniusza)

- kółko całkujące (połączone jest z mechanizmem łączącym jego obroty; skład: noniusz, bęben,

tarcza pozioma).

Sposób pomiaru: Biegun planimetru ustawia się na zewnątrz lub wewnątrz figury (lepiej wewnątrz), której powierzchnia ma być zmierzona, po czym wodzikiem oprowadza się daną figurę dookoła po jej konturze. Z licznika planimetru odczytuje się ilość obrotów kółka całkującego.

P = C₁ ∙ n

P - powierzchnia

C₁ - stała planimetru

n - ilość obrotów kółka (różnica odczytów przed i po oprowadzeniu danej figury → n=O₂ - O₁)

Wyznaczanie stałej planimetru C₁:

• zależy od długości ramienia wodzącego (przede wszystkim)

• zależy od gatunku papieru (minimalnie)

Wyznaczanie stałej planimetru C₁ polega na zmierzeniu za pomocą planimetru powierzchni takiej figury, której wielkość pola jest znana (np. kwadrat o boku 10cm).

P_zn - powierzchnia znana

W celu wyznaczenia stałej planimetru C₁ z większą dokładnością, powierzchnię znaną obwodzi się wielokrotnie w dwóch położeniach planimetru.

W B W

I położenie II położenie

B

Zmieniając odpowiednio długości ramienia wodzącego można uzyskać żądaną wartość stałej C₁.

Wyznaczanie stałej planimetru C₁ w żądanych jednostkach z uwzględnieniem skali mapy:

np.: chcemy wyznaczyć C₁ w m² dla mapy w skali 1:M

DANE: P_zn w m², n=O₂ - O₁

np.: P_zn=10 000mm², skala 1:500, n=1000

- stała z dokładnością do czterech miejsc po przecinku

Uwagi dotyczące pomiaru powierzchni planimetrem kompensacyjnym:

• powierzchnia rysunkowa mapy ma być płaszczyzną gładką i poziomą

• stałą C₁ należy wyznaczać na papierze, na którym wykreślona jest mapa

• biegun należy umieścić w takim miejscu, aby kółko całkujące i kompensacyjne toczyły się przy obwodzeniu zawsze po arkuszu mapy

• kąt pomiędzy promieniem wodzącym i biegunowym musi mieścić się w granicach 30º<α<150º

• należy obrać taki punkt wyjściowy wodzika, aby kółko całkujące toczyło się powoli, a nawet ślizgało się bez zmiany odczytów przy rozpoczęciu i kończeniu obwodzenia

• wodzik należy prowadzić ruchem jednostajnym starając się nie zbaczać z konturu mierzonej figury (nie przy linijce!!!)

• figurę należy obwodzić wielokrotnie w dwóch położeniach bieguna (około 5 razy)

• duże figury, których nie można objąć ramieniem wodzącym planimetru przy jednym położeniu bieguna, należy dzielić na części i planimetrować kolejno.

---