dr inż. Marian Poniewiera

marzec 2007

Materiały powielane powstały na podstawie wykładów pracowników Zakładu Geodezji i Ochrony Terenów Górniczych Pol. Śl.
w Gliwicach oraz na podstawie literatury i nie stanowią publikacji w rozumieniu ustawy o prawach autorskich.

PODSTAWY OBLICZEŃ GEODEZYJNYCH

W teorii pomiarów wyróżnia się następujące określenia wielkości mierzalnych:

•

wielkość projektowana (nominalna),

•

wielkość tolerowana,

•

wielkość graniczna,

•

wielkość rzeczywista,

•

wielkość zmierzona (metrologiczna).

Różnice między tymi wielkościami nazywamy odchyłkami i odróżniamy: odchyłki dopuszczalne
(mieszczące się w granicach norm lub przepisów) i odchyłki niedopuszczalne ( nie mieszczące się
w w/w granicach).

Przedział ufności
P(x

0

– tm < x< x

0

+ tm) = 1 – α

α – współczynnik istotności
1 – α – współczynnik ufności
t – parametr odczytywany z tablic rozkładu normalnego dla zadanego poziomu ufności,
m – błąd średni.

Trzy podstawowe grupy błędów:

•

błędy grube, czyli pomyłki lub pomiar wykonany niewłaściwie,

•

błędy systematyczne,

•

błędy przypadkowe (losowe).

Źródłem błędów pomiaru są:

•

niedokładność zmysłów obserwatora,

•

niedokładność narzędzi pomiarowych,

•

wpływ warunków zewnętrznych.

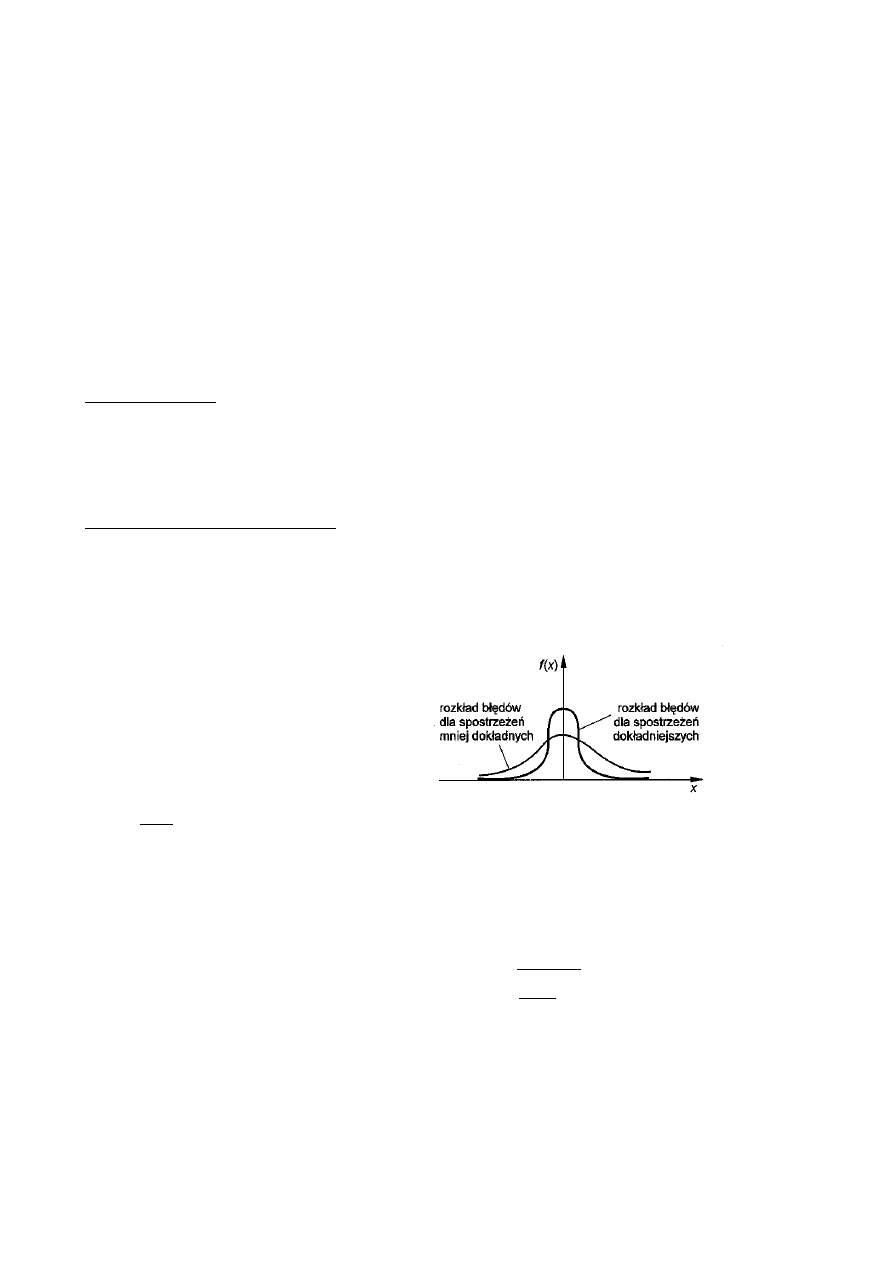
Rozkład błędów losowych (spostrzeżeń)

Wielkość najprawdopodobniejsza

X

śr

=

[

X

i

]

n

Błąd pozorny – różnica między wielkością najprawdopodobniejszą X

śr

, a poszczególnymi

spostrzeżeniami X

i

.

=X

śr

− X

i

Metoda najmniejszych kwadratów

Średni błąd pojedynczego pomiaru m

0

[νν] = min

m

0

=



[



]

n

−1

1

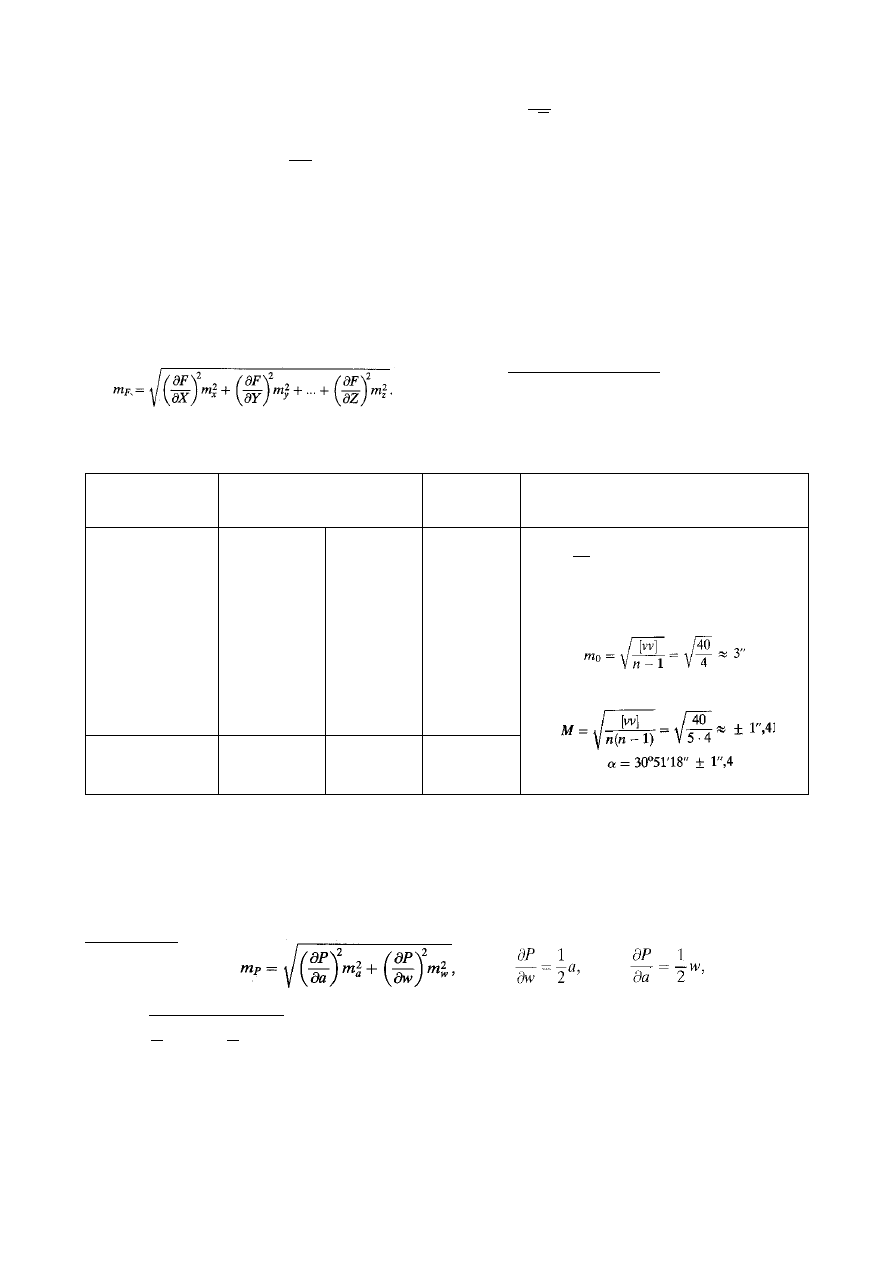
Średni błąd średniej arytmetycznej z n pomiarów

Błąd przeciętny

Błąd graniczny – jest równy trzem błędom średnim
M

max

= 3m

Błąd średni sumy (lub różnicy) wielkości mierzonych
F = x

1

± x

2

± x

3

± ... ± x

n

Średni błąd funkcji F = f(X, Y,..., Z)

Obliczenie najprawdopodobniejszej wartości kąta i wartości błędu średniego

Rezultaty

pomiarów

a

i

n

i

= x

śr

-

a

i

nn

Obliczenia

30

0

51

′

14"

20"
18"

22"
16"

+

-

-

+

4"

2"

0

4"
2"

16

4
0

16

4

Σ

a

ι

= 90

"

Σ

n = 0

40



śr

=



i

n

=30

0

51

'

18

' '

Błąd średni pojedynczego
spostrzeżenia

Błąd średni średniej arytmetycznej

Przykład. Z jakim błędem średnim można wyznaczyć pole trójkąta, jeżeli wysokość w = 40 m
(zadanie wykonać także dla w = 20+n, gdzie n<1,30>) pomierzono z błędem średnim m

w

= 0,02 m,

zaś podstawę a = 60 m pomierzono z błędem średnim m

a

= ± 0,03 m, a wiadomo że P = aw/2.

Rozwiązanie:

m

P

=



1
4

w

2

m

a

2



1
4

a

2

m

w

2

=0,85 m

2

2

m

F

=



m

1

2

m

2

2

m

3

2

...m

n

2

M

=

m

0



n

d

=

[



]

n

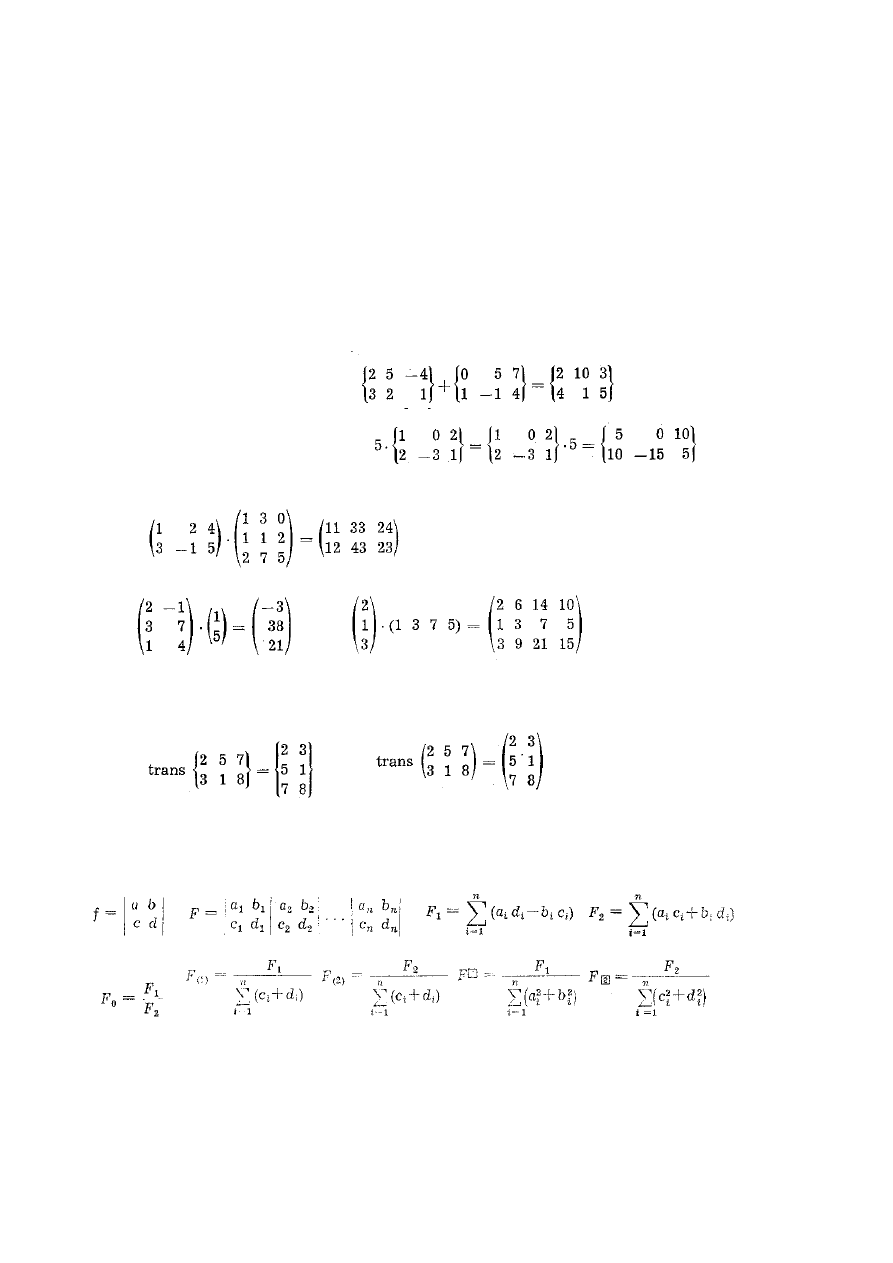
Tolerancja budowlana-
Jest to różnica między projektem a realizacją
(dl)

2

= (dl

t

)

2

+ (dl

b

)

2

gdzie: dl

t

– tyczenia, dl

b

– prac budowlanych

dl

t

= dl

b

= 0,7 dl

Aby uzyskać błąd graniczny należy uwzględnić poziom ufności
m

t

 dl

t

/r, gdzie r – poziom ufności

r = 2 p = 95%

r = 2,5 p = 98%

r = 3 p = 99%

dla

r = 2,5 m

t

= 0,28 dl ±4

Dodawanie, mnożenie i transpoza macierzy
Dodawanie macierzy

Mnożenie macierzy przez liczbę

Iloczyn dwóch macierzy

Transpoza macierzy

Wzory rachunkowe Hausbrandta

3

25,40

59,45

52,70

12,10

35.33
27.37

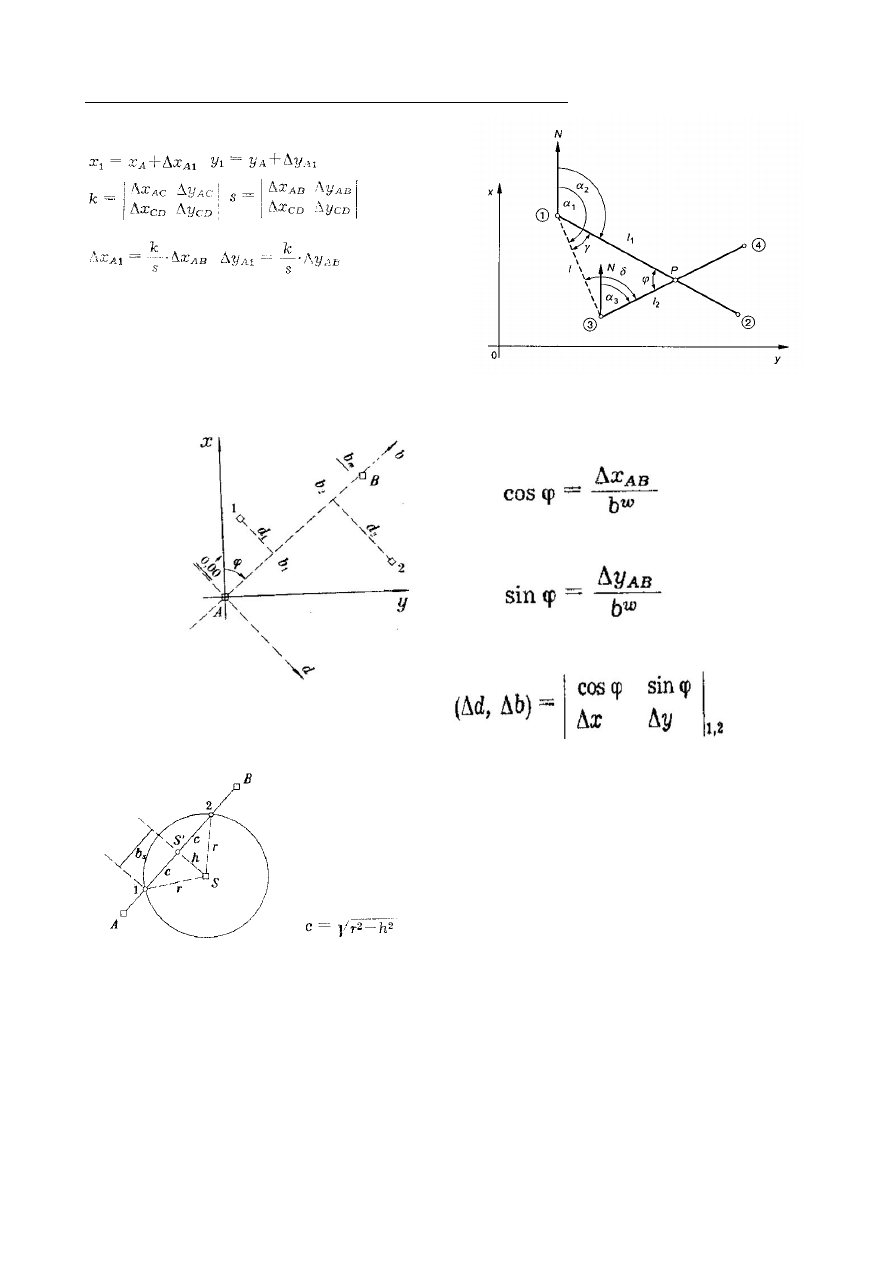
Wyznaczenie współrzędnych punktu przecięcia się dwóch prostych

Rzutowanie punktów na prostą

Przecięcie okręgu prostą

Literatura:
1. Przewłocki S.: Geodezja dla kierunków niegeodezyjnych. Wydawnictwo Naukowe PWN,

Warszawa 2002r.

2. Hausbrandt S.: Rachunek wyrównawczy i obliczenia geodezyjne. Tom I. Państwowe

Przedsiębiorstwo Wydawnictw Kartograficznych, Warszawa 1970.

4