PODSTAWY OBLICZEŃ

GEODEZYJNYCH

dr inż. Marian Poniewiera

marzec 2007 r.

Wielkości mierzalne

●

wielkość projektowana (nominalna),

●

wielkość tolerowana,

●

wielkość graniczna,

●

wielkość rzeczywista,

●

wielkość zmierzona (metrologiczna).

Odchyłki

●

odchyłki dopuszczalne - mieszczące się

w granicach norm lub przepisów

●

odchyłki niedopuszczalne - nie mieszczące się

w w/w granicach

Przedział ufności

P(x

0

– tm < x< x

0

+ tm) = 1 – α

α

– współczynnik istotności,

1 – α

– współczynnik ufności,

t

– parametr odczytywany z tablic rozkładu normalnego dla

zadanego poziomu ufności,

m

– błąd średni.

Podstawowe grupy błędów

●

błędy grube, czyli pomyłki lub pomiar wykonany

niewłaściwie,

●

błędy systematyczne,

●

błędy przypadkowe (losowe).

Źródła błędów

●

niedokładność zmysłów obserwatora,

●

niedokładność narzędzi pomiarowych,

●

wpływ warunków zewnętrznych.

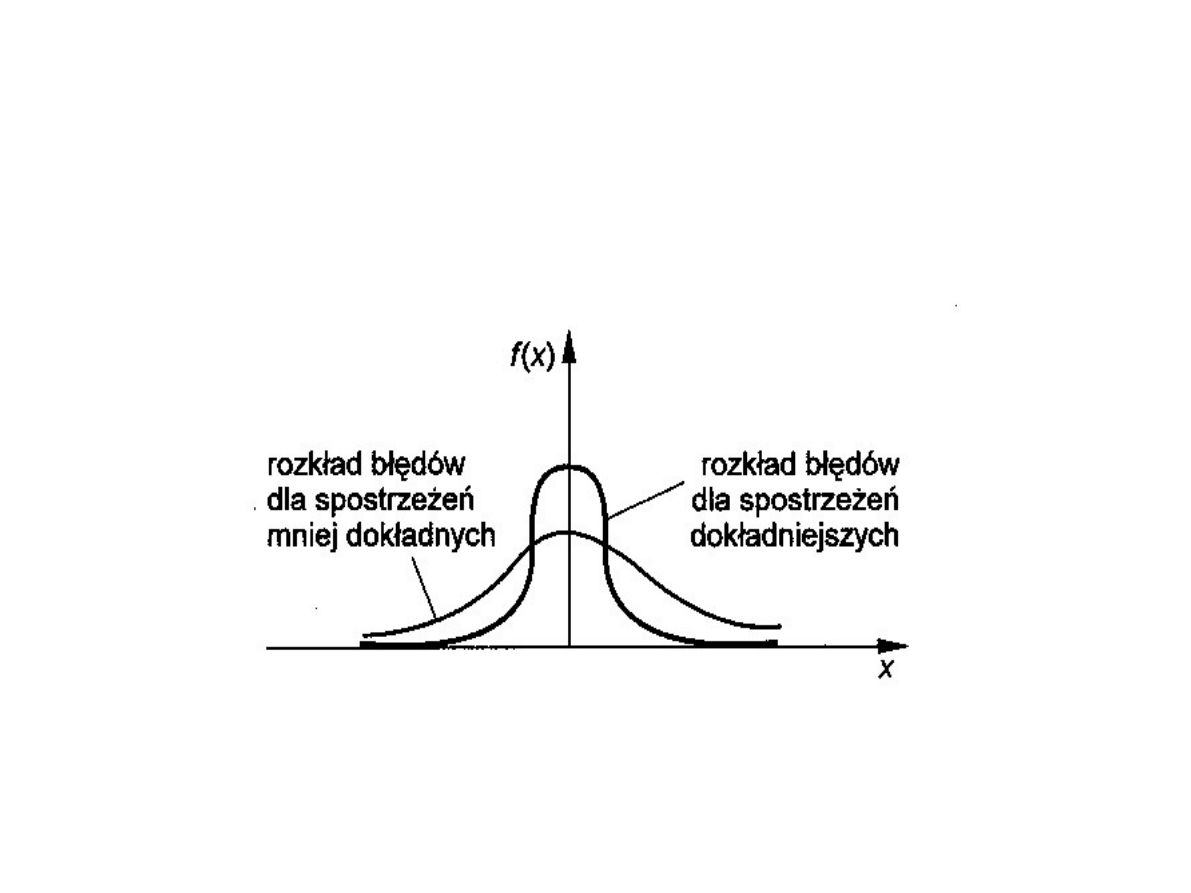
Rozkład błędów losowych

Wielkość najprawdopodobniejsza

X

śr

=

[

X

i

]

n

Błąd pozorny

=X

śr

−X

i

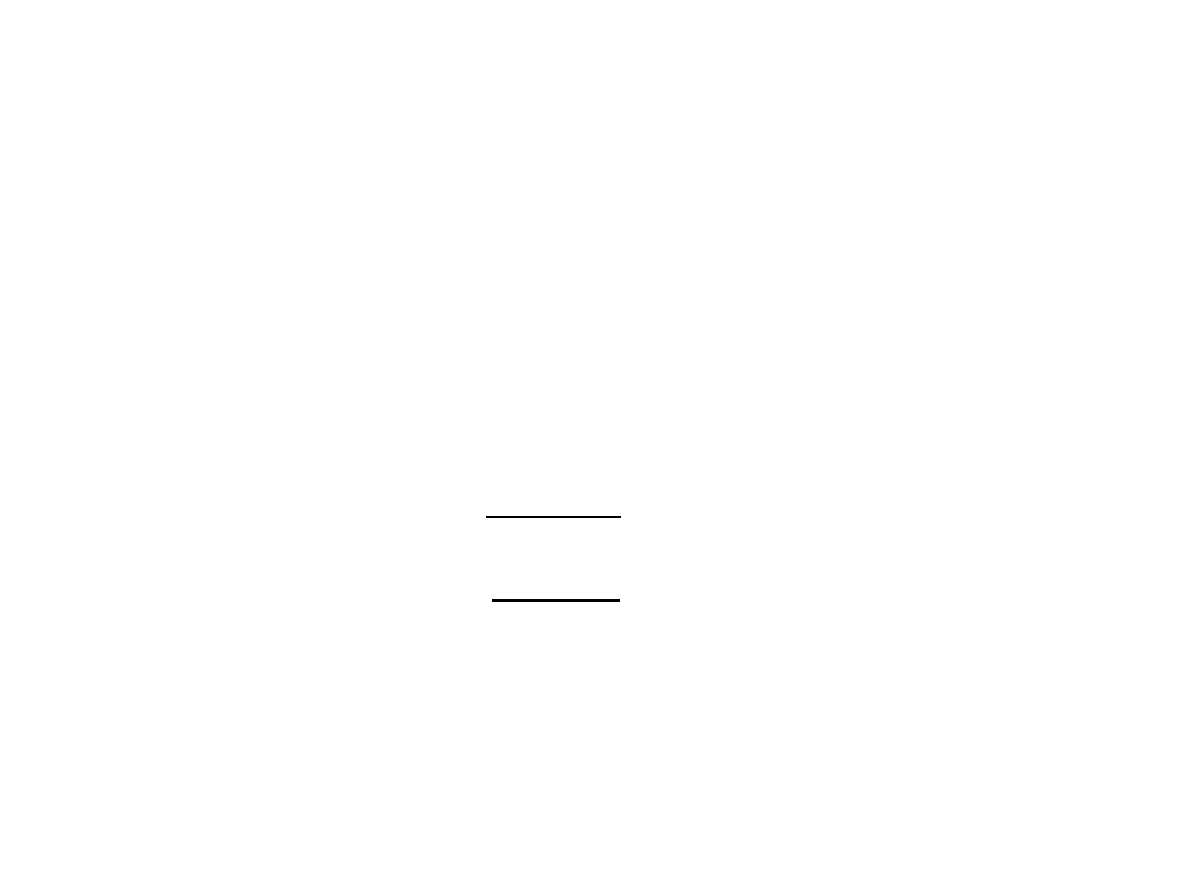
Metoda najmniejszych kwadratów

[νν] = min

Średni błąd pojedynczego pomiaru m

0

m

0

=



[



]

n−1

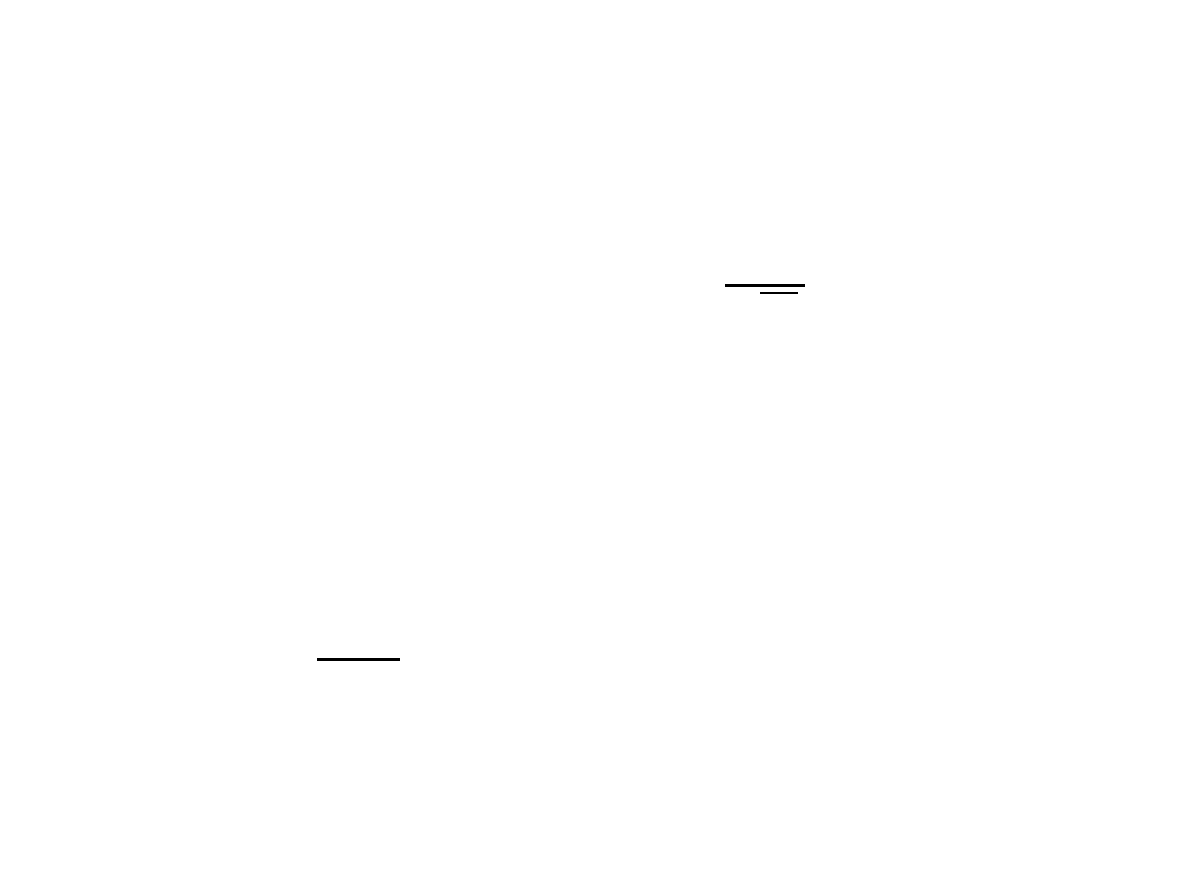
Średni błąd średniej arytmetycznej

z n pomiarów

M

=

m

0



n

Błąd przeciętny

d

=

[



]

n

Błąd graniczny

M

max

= 3m

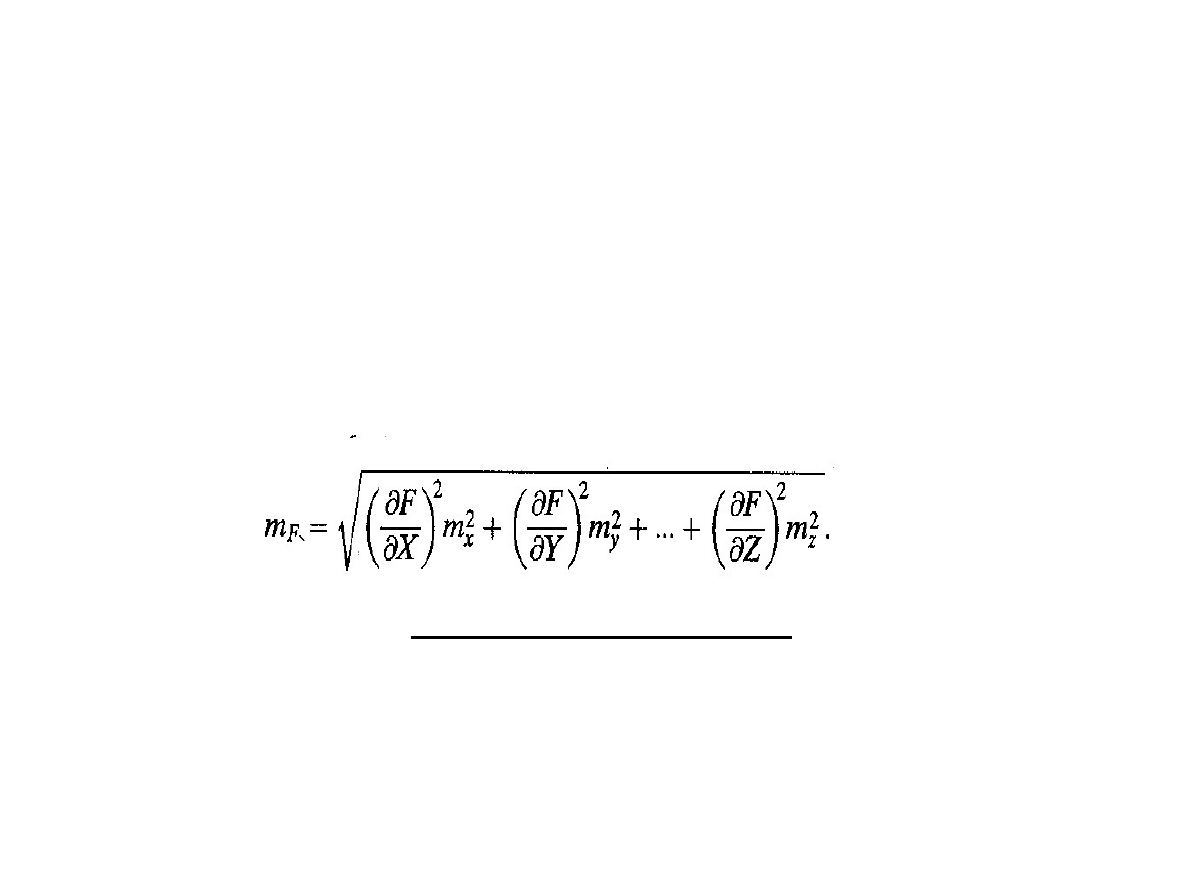
Błąd średni sumy (lub różnicy) wielkości
mierzonych

F = x

1

± x

2

± x

3

± ... ± x

n

Średni błąd funkcji F = f(X, Y,..., Z)

m

F

=



m

1

2

m

2

2

m

3

2

...m

n

2

Obliczenie najprawdopodobniejszej wartości

kąta i wartości błędu średniego

Rezultaty

pomiarów

a

i

n

i

= x

śr

-

a

i

nn

Obliczenia

30

0

51

′

14"

20"
18"

22"
16"

Obliczenie najprawdopodobniejszej wartości

kąta i wartości błędu średniego

Rezultaty

pomiarów

a

i

n

i

= x

śr

-

a

i

nn

Obliczenia

30

0

51

′

14"

20"
18"

22"
16"

+

-

-

+

4"

2"

0

4"
2"

16

4
0

16

4

Σ

a

ι

= 90

"

Σ

n = 0

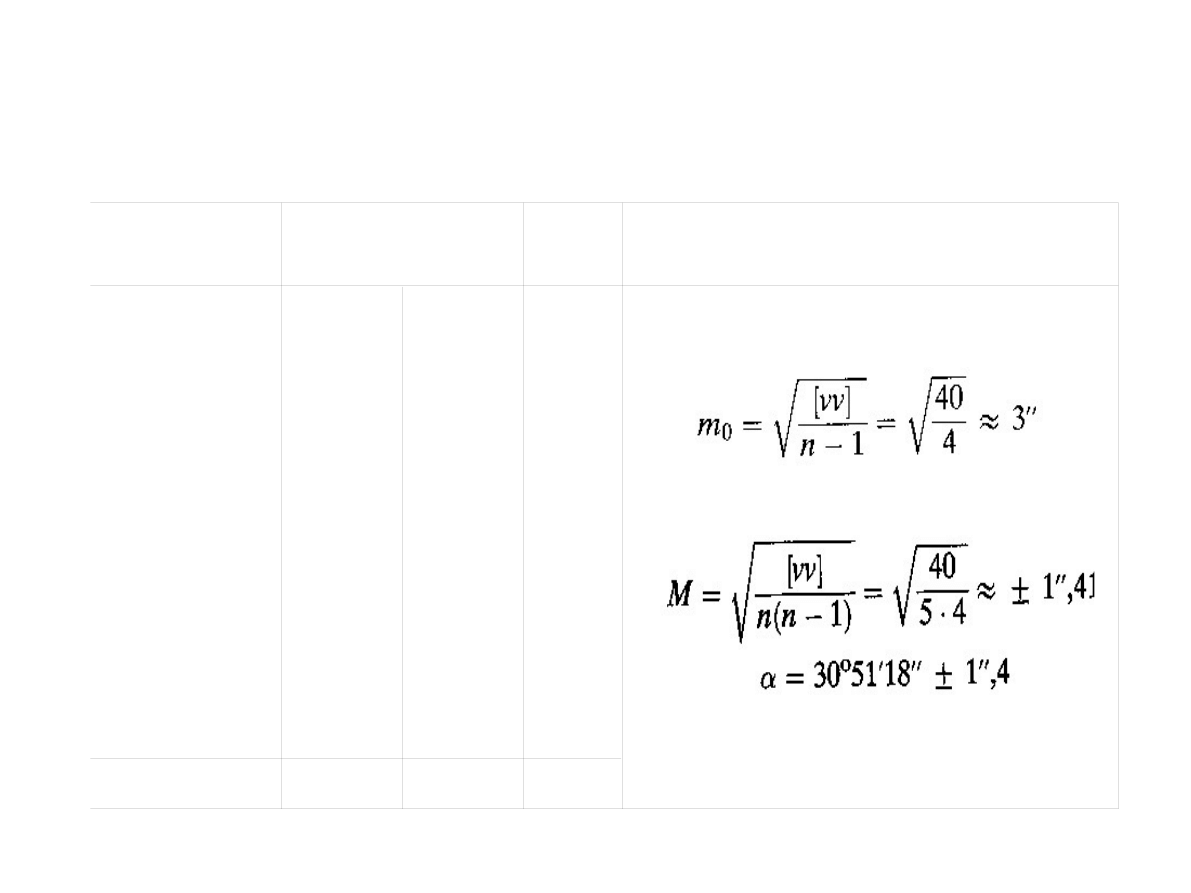
Błąd średni pojedynczego spostrzeżenia

Błąd średni średniej arytmetycznej

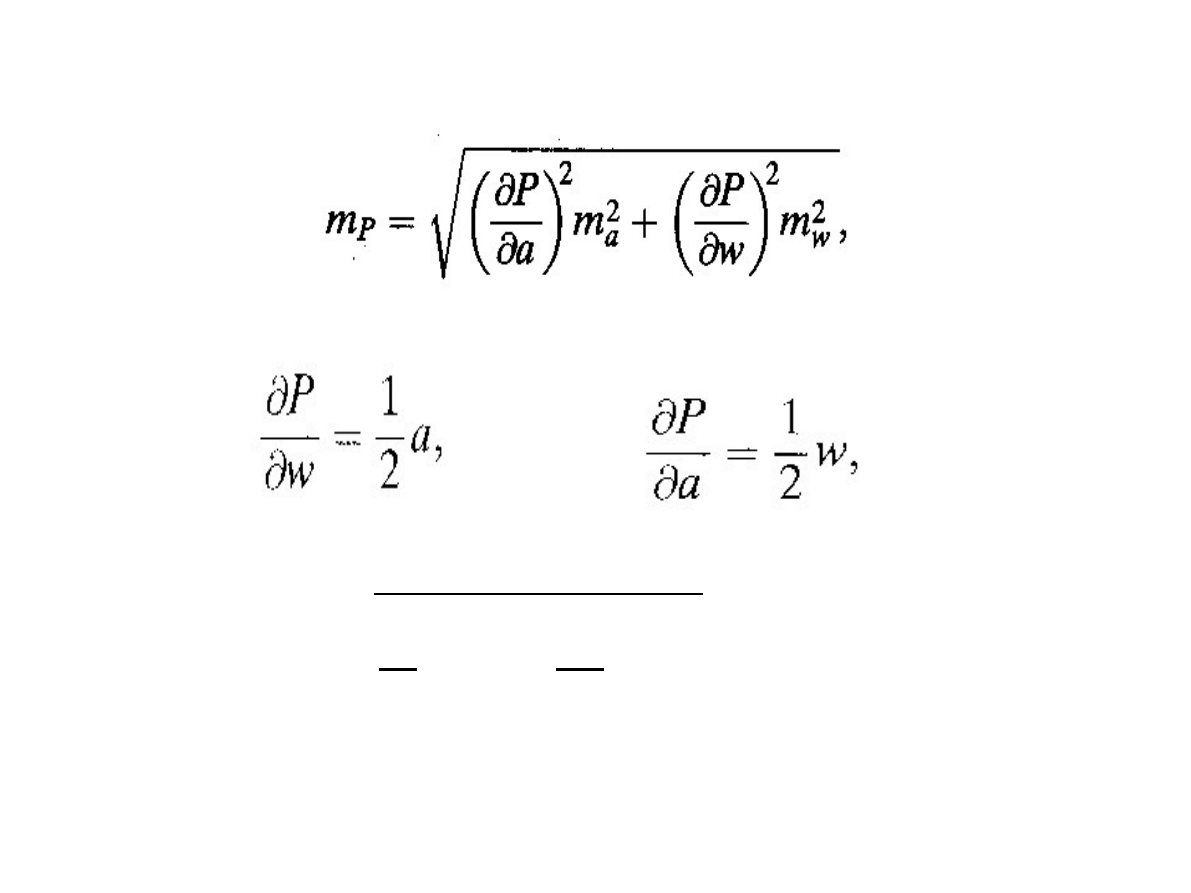
Przykład. Z jakim błędem średnim można wyznaczyć
pole trójkąta, jeżeli wysokość w=40 m (zadanie wykonać
także dla w=20+n, gdzie n<1,30>) pomierzono
z błędem średnim m

w

= 0,02m, zaś podstawę a=60m

pomierzono z błędem średnim m

a

=±0,03m,

a wiadomo że P = aw/2.

m

P

=



1

4

w

2

m

a

2



1

4

a

2

m

w

2

=0,85 m

2

dla w=20+n, gdzie n<1,30> m

P

wynosi

n

m

P

n

m

P

n

m

P

1

0,68

11

0,76

21

0,86

2

0,68

12

0,77

22

0,87

3

0,69

13

0,78

23

0,88

4

0,70

14

0,79

24

0,89

5

0,71

15

0,80

25

0,90

6

0,72

16

0,81

26

0,91

7

0,72

17

0,82

27

0,93

8

0,73

18

0,83

28

0,94

9

0,74

19

0,84

29

0,95

10

0,75

20

0,85

30

0,96

Tolerancja budowlana

Różnica między projektem a realizacją

(dl)

2

= (dl

t

)

2

+ (dl

b

)

2

gdzie: dl

t

– tyczenia, dl

b

– prac budowlanych

dl

t

= dl

b

= 0,7 dl

Aby uzyskać błąd graniczny należy uwzględnić poziom ufności

m

t

 dl

t

/r,

gdzie r – poziom ufności

r = 2 p = 95% r = 2,5 p = 98%

r = 3 p = 99%

dla r = 2,5 m

t

= 0,28 dl ±4

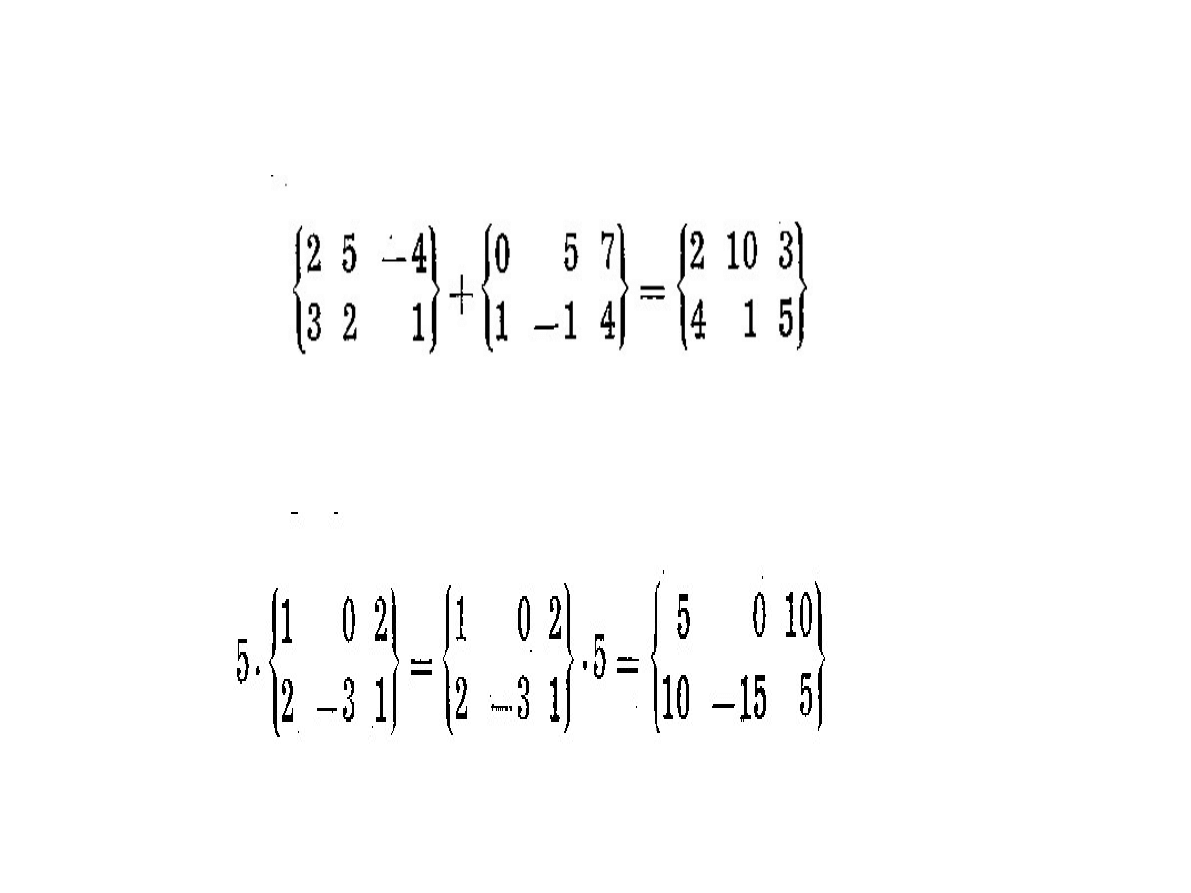
Dodawanie macierzy

Mnożenie macierzy przez liczbę

Iloczyn dwóch macierzy

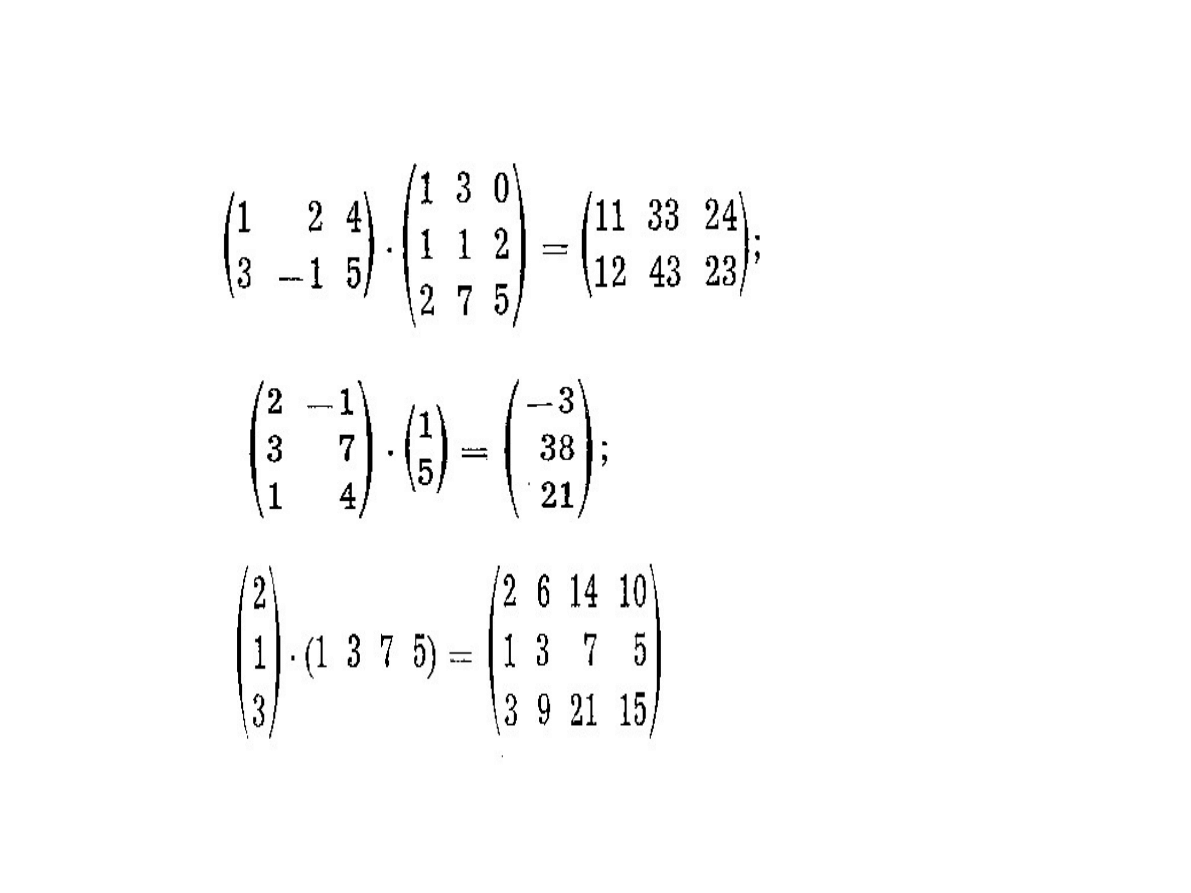
Iloczyn dwóch macierzy

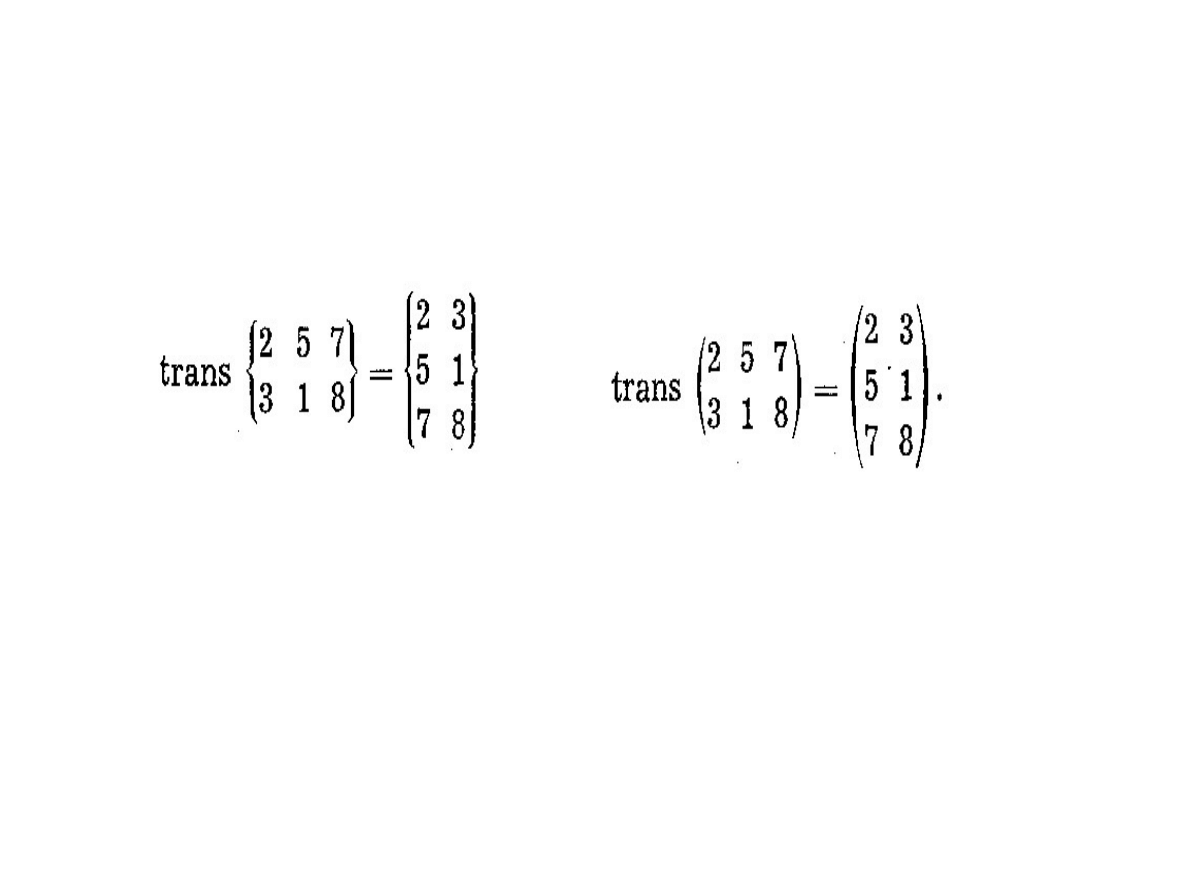
Transpoza macierzy

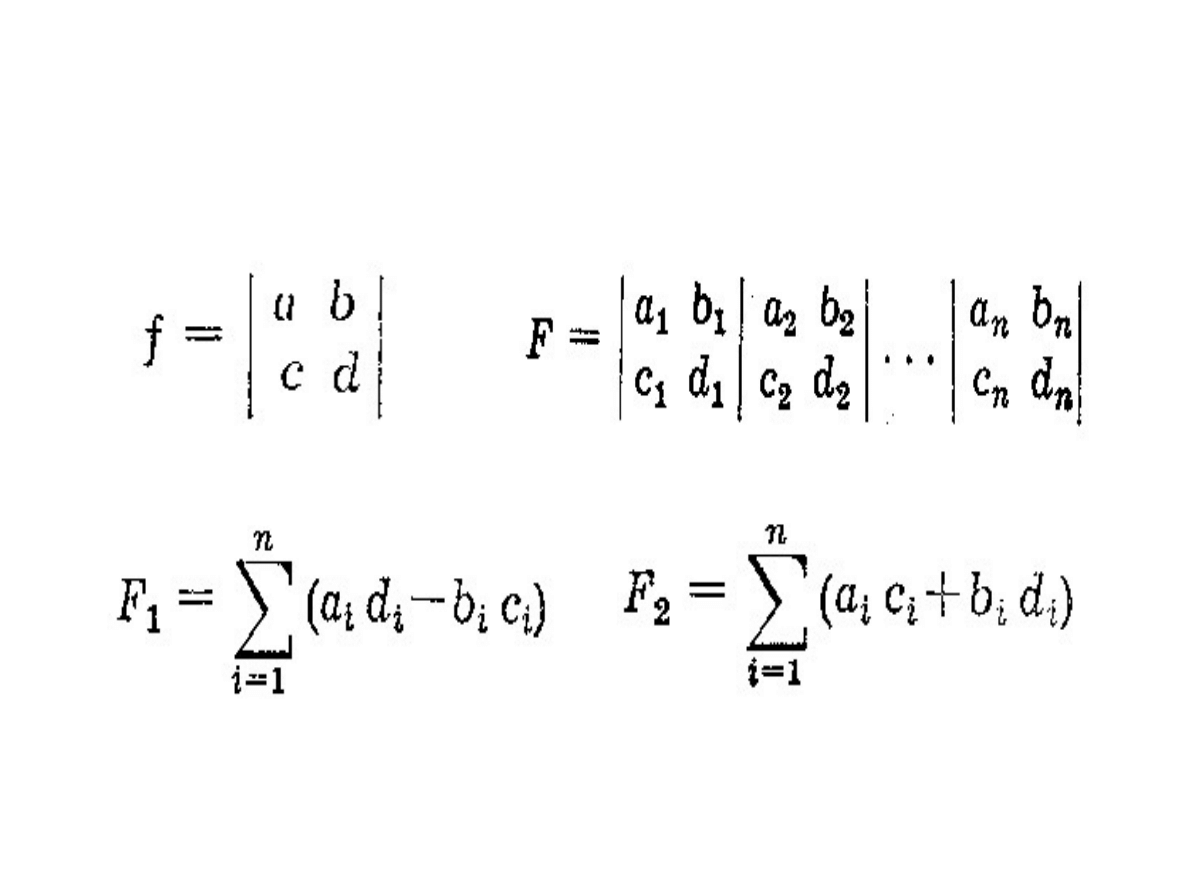
Wzory rachunkowe Hausbrandta

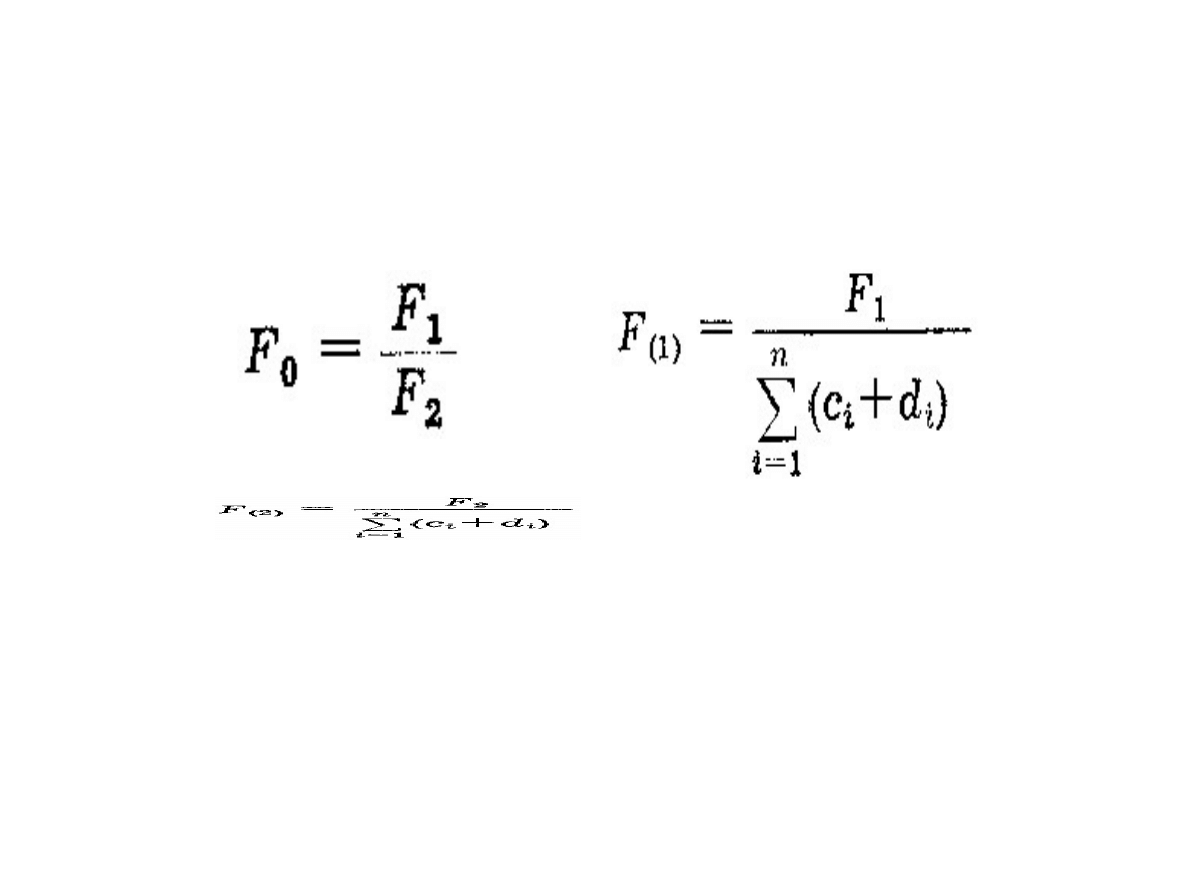
Wzory rachunkowe Hausbrandta

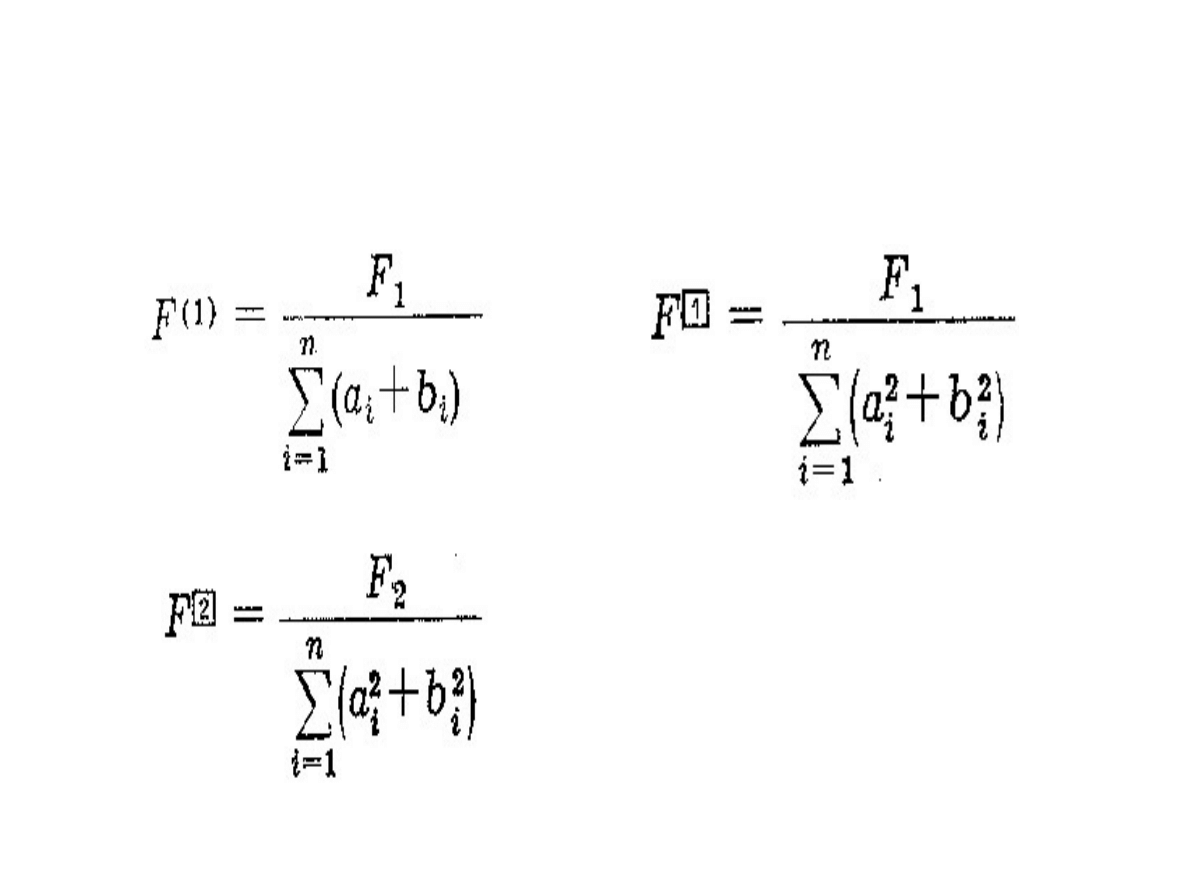
Wzory rachunkowe Hausbrandta

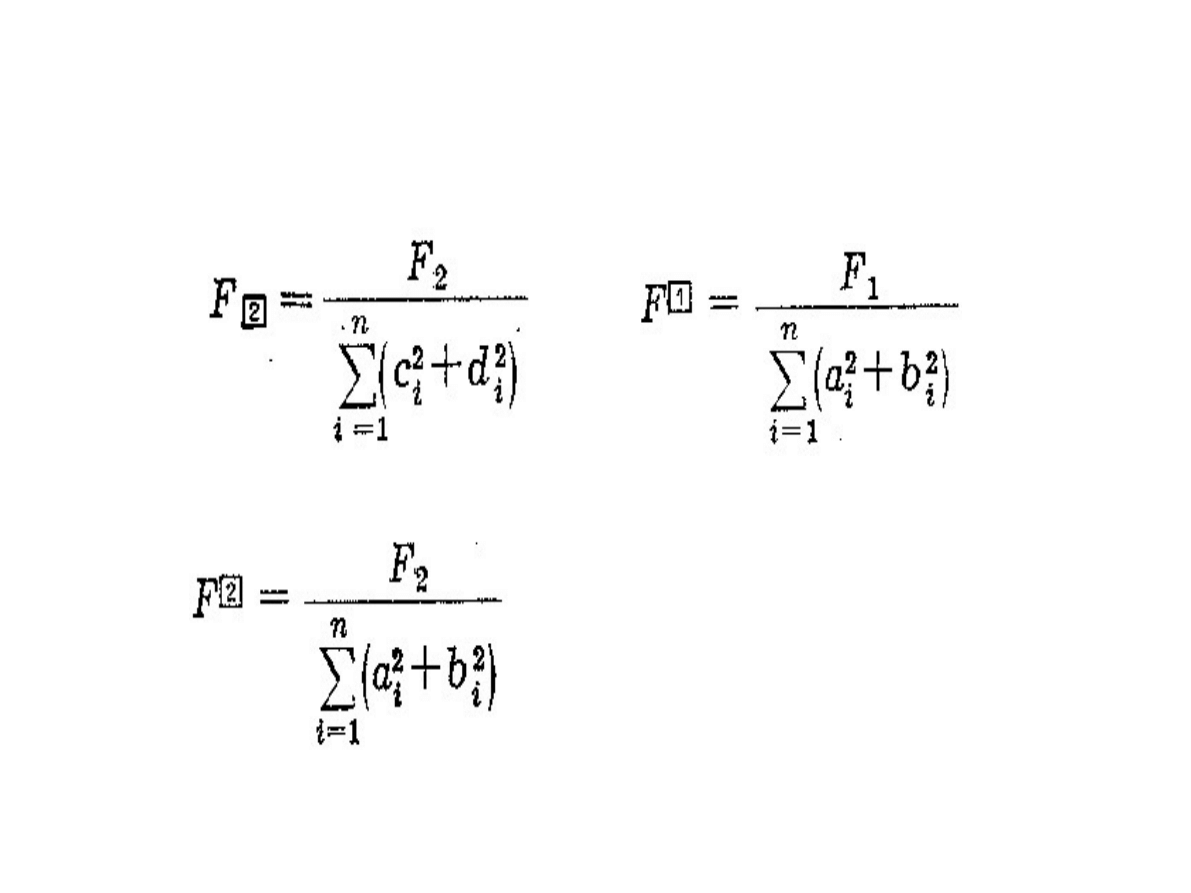
Wzory rachunkowe Hausbrandta

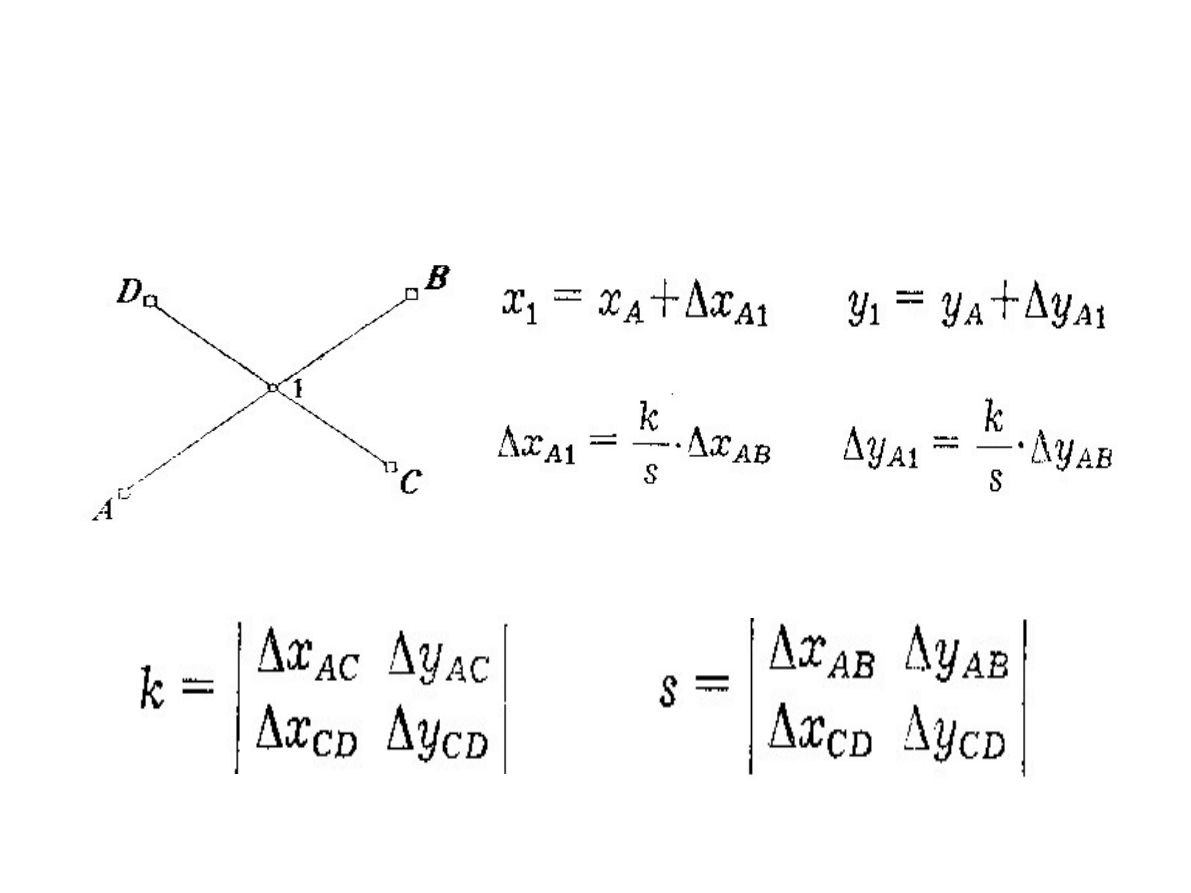
Przecięcie dwóch prostych,

znane punkty ABCD

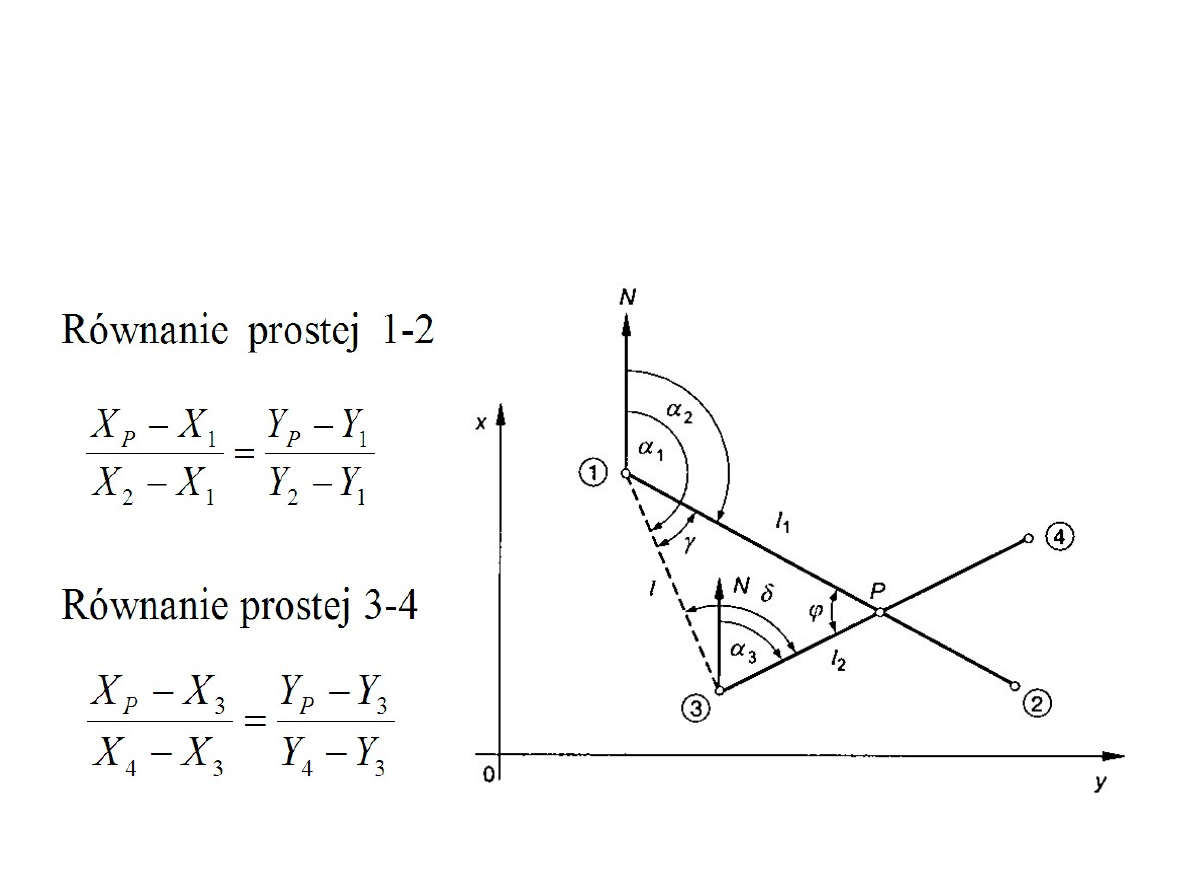
Wyznaczenie współrzędnych punktu

przecięcia się dwóch prostych

25,40

59,45

52,70

12,10

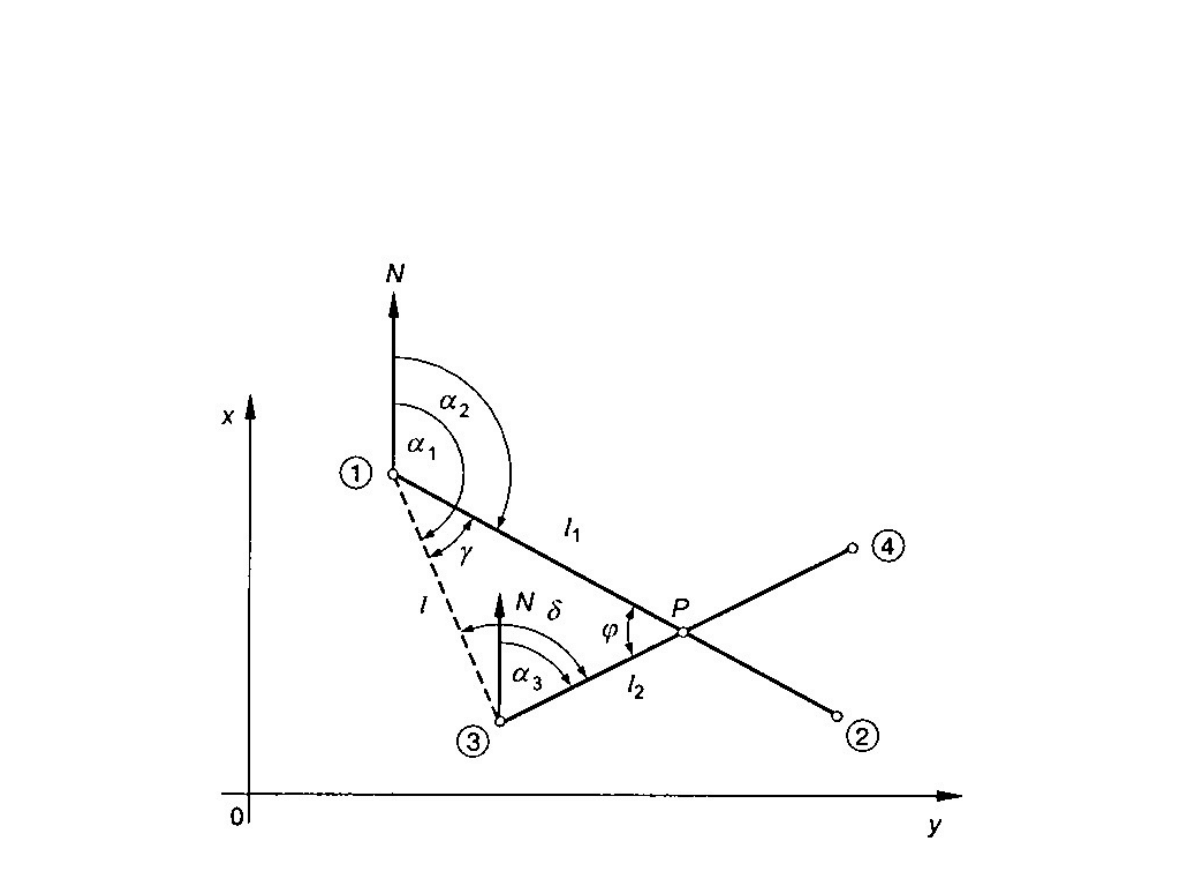
Wyznaczenie współrzędnych punktu przecięcia

się dwóch prostych

25,40

59,45

52,70

12,10

35.33
27.37

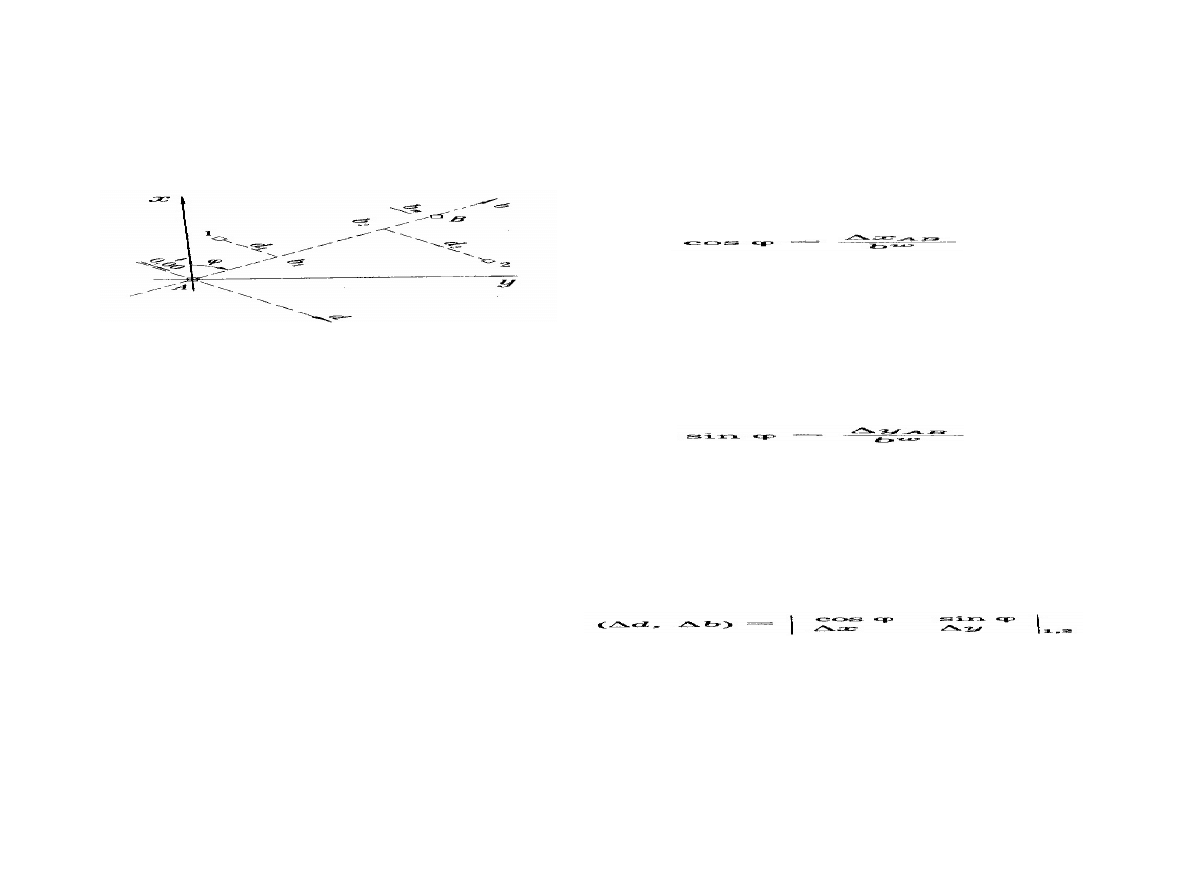
Rzutowanie punktów na prostą

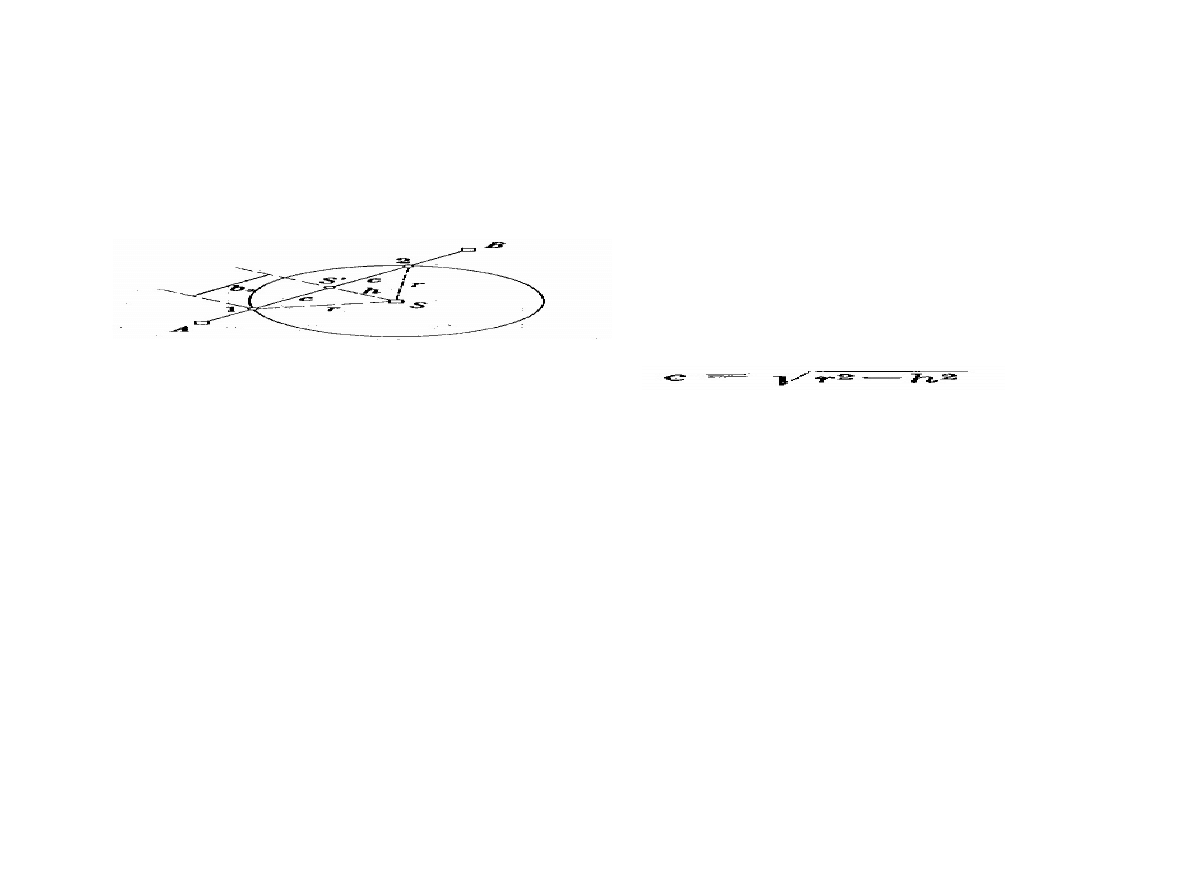
Przecięcie okręgu prostą

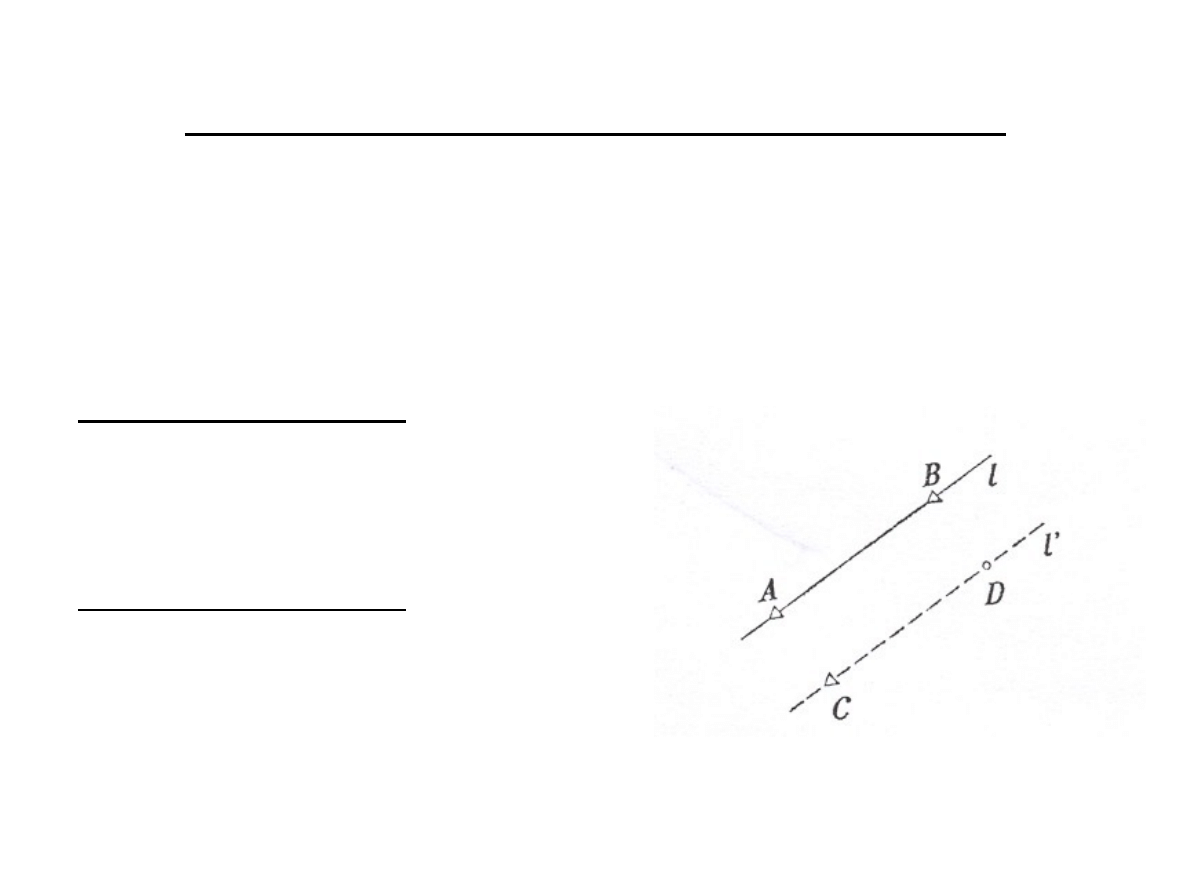
Wyznaczenie prostej równoległej do danej

Dane są współrzędne punktów A, B, C, z których punkty A i B
wyznaczają prostą l. Obliczyć współrzędne wybranego punktu D
leżącego na prostej l' (C, D) równoległej do l.

Wzory rozwiązujące

:

x

D

= - x

A

+ x

B

+ x

C

y

D

= - y

A

+ y

B

+ y

C

Wzory kontrolujące:

∆

x

CD

=

∆

x

AB

∆

y

CD

=

∆

y

AB

Wyznaczenie prostej równoległej do danej

Nr punktu

Współrzędne

Przyrosty

x

y

∆

x

∆

y

A

 

B
C

 

D

102,31

 

508,64

-106,53

 
 

200,15

 

802,67
901,18

 
 

 
 
 
 
 

 
 
 
 
 
 

Wyznaczenie prostej równoległej do danej

Nr punktu

Współrzędne

Przyrosty

x

y

∆

x

∆

y

A

 

B
C

 

D

102,31

 

508,64

-106,53

 

299,80

200,15

 

802,67
901,18

 

1503,70

 

406,33

 
 

406,33

 
 

602,52

 

 

602,52

 

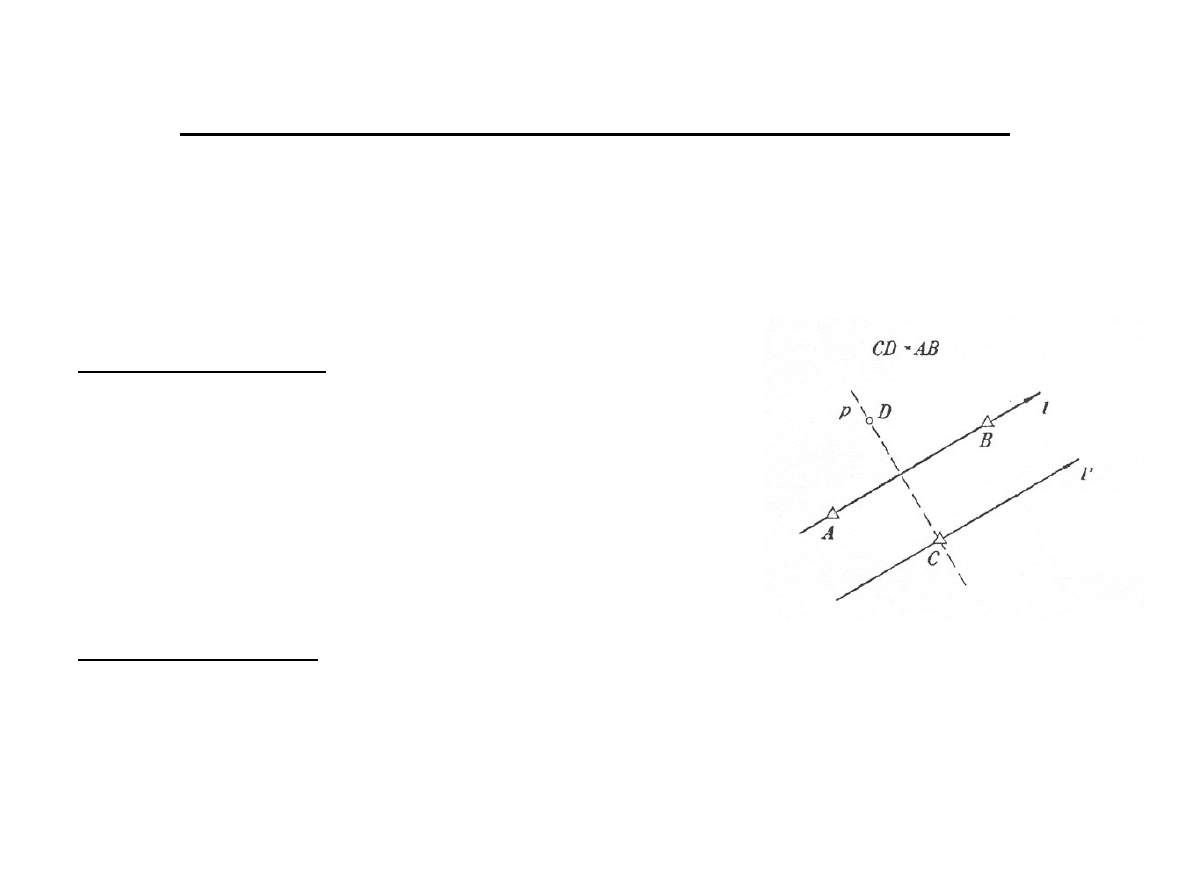
Wyznaczanie prostej prostopadłej do danej

Dane są współrzędne punktów A, B, C, z których punkty A i B wyznaczają prostą l.
Obliczyć współrzędne wybranego punktu D prostej p (C, D) prostopadłej do l (A, B).

Wzory rozwiązujące :
punkt D z lewej strony prostej l’:
x

D

= - y

A

+ y

B

+ x

C

y

D

= x

A

- x

B

+ y

C

'

punkt D z prawej strony prostej l‘:
x

D

= y

A

- y

B

+ x

C

y

D

= - x

A

+ x

B

+ y

C

Wzory kontrolujące:

punkt D z lewej strony prostej l‘:

-

∆

x

AB

=

∆

y

CD

∆

y

AB

=

∆

x

CD

punkt D z prawej strony prostej l‘:

∆

x

AB

=

∆

y

CD

-

∆

y

AB

=

∆

x

CD

Wyznaczanie prostej prostopadłej do danej

Punkt D położony z lewej strony prostej l'

Nr punktu

Współrzędne

Przyrosty

x

y

∆

x

∆

y

A

 

B
C

 

D

102,31

 

508,64

-106,53

 
 

200,15

 

802,67
901,18

 
 

 
 
 
 

 
 
 
 
 
 

Wyznaczanie prostej prostopadłej do danej

Punkt D położony z lewej strony prostej l'

Nr punktu

Współrzędne

Przyrosty

x

y

∆

x

∆

y

A

 

B
C

 

D

102,31

 

508,64

-106,53

 

495,99

200,15

 

802,67
901,18

 

494,85

 

-406,33

 
 

602,52

 
 

602,52

 
 

-406,33