1.Wstęp

Projekt przedstawia prognozowanie ilości absolwentów szkół wyższych w latach 1999 -2003.

Prognoza ta umożliwi sprawdzenie w jaki sposób będzie kształtować się stan wykształcenia w Polsce w najbliższej przyszłości, pozwolą na porównanie w jakim tempie wzrasta liczba osób wykształconych i jakie to ma skutki na rozwój, gospodarkę i uprzemysłowienie kraju.

Na podstawie danych o ilości absolwentów szkół wyższych możemy sprawdzić dynamikę wzrostu wykształcenia w Polsce. Możemy określić wskaźnik wzrostu wykształcenia naszego społeczeństwa w odniesieniu do innych krajów europejskich.

2. Dane źródłowe.

Dane o ilości absolwentów szkół wyższych zaczerpnięto z Małego Rocznika Statystycznego z 1999 roku, wydanego przez Główny Urząd Statystyczny w Warszawie 1998.

Dane te przedstawiono w tabeli 1, a graficznie na wykresie 1.

Tabela1.

Dane źródłowe dotyczące ilości absolwentów szkół wyższych

[absolw./ 10000 mieszk.] w latach 1991 do 1998 .

Lata	1991	1992	1993	1994	1995	1996	1997	1998
Absolwenci	15,3	16	16,7	18,1	20	29,8	36,7	44

MAŁY ROCZNIK STATYSTYCZNY

Wykres 1 . Graficzne przedstawienie danych statystycznych dotyczących

ilości absolwentów szkół wyższych [absolw./ 10000 mieszk.]

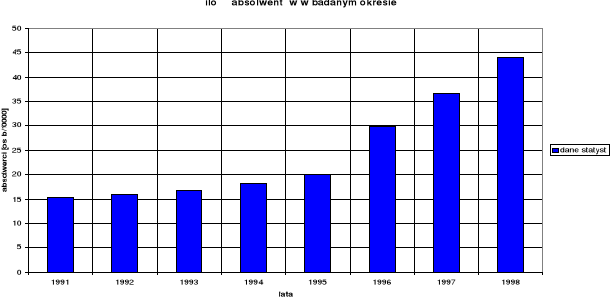
MAŁY ROCZNIK STATYSTYCZNY

W latach 1991 -1995 wzrost liczby absolwentów szkół wyższych jest niewielki i stosunkowo wolno przyrasta 15.3 do 20 absolwentów na każde 10000 mieszkańców Polski.

W latach 1996 -1998 następuje niemal podwojenie liczby absolwentów w przeciągu zaledwie trzech lat z 29,8 w 1996 do 44 absolwentów na 10000 mieszkańców w 1998.

Tak duży przyrost może być związany wyżem demograficznym przypadającym na lata 1975 - 1979, jak również może być wynikiem przemian zachodzących w naszym kraju ( wzrost bezrobocia, wyższe wymagania pracodawców wobec pracowników).

3 Prognozowanie

A. Metody badawcze

Rozróżnia się kilka rodzajów prognozowania zjawisk gospodarczych między innymi prognozowanie demograficzne, społeczne, naukowo -techniczne, gospodarcze.

Wśród metod prognostycznych rozróżniamy:

• metody intuicyjne

• metody kolejnych przybliżeń

• metody analogii

• metody prognozowania statystycznego .

Ta ostatnia metoda oparta na modelach ekonometrycznych , dokładnie na klasycznych modelach trendu jest wykorzystana do prognozowania w projekcie.

2. Regresja i korelacja

Rozpatrywano kolejno modele:

• regresja liniowa

• regresja wykładnicza

• regresja hiperboliczna

• regresja potęgowa

• regresja logarytmiczna

Poniżej każdy z modeli został omówiony.

Do obliczeń wykorzystywano kalkulator naukowy, arkusze kalkulacyjne Microsoft Excel.

C. Obliczenia

Wyniki przeprowadzonych badań zestawiono w tabeli 2.

Tabela 2. Zestawienie poszczególnych modeli wraz z równaniami

szczegółowymi.

Model	Współczyn korelacji R	Równanie szczegółowe	Jedno stka
Liniowy Y=a+b*X	0,92	LASW =6,06+4,11*(kol. bad. rok ^1- 1990)	absolw. / 10 tys. mieszk.
Wykładniczy Y=a*b^X	0,95	LASW =11,097*1,17*^(kol. bad. rok - 1990)	absolw. / 10 tys. mieszk.
Hiperboliczny Y=a+b/X	-0,61	LASW = 32,27+ (kol. bad. rok. - 1990)* (- 22,66)	absolw. / 10 tys. mieszk.
Potęgowy Y=a*X^b	0,83	LASW =11,91*(kol. bad. rok- 1990) ^0,49	absolw. / 10 tys. mieszk.
Logarytmiczny Y=a=+b*logX	0,79	LASW =8,34+28,2*log (kol. bad. rok - 1990)	absolw. / 10 tys. mieszk.

Tabela 2. Zawiera równanie ogólne dla poszczególnych modeli, współczynnik korelacji, oraz równanie szczegółowe na którym oparte jest prognozowanie liczby absolwentów na lata 1999 - 2003.

Tabela 3. Przedstawia prognozy według poszczególnych modeli

Rok	Prognoza liniowa	Prognoza wykładnicza	Progn. hiperbol.	Prognoza potęgowa	Prognoza logarytmiczna
1999	43,05	46,30	29,75	34,95	35,25
2000	47,16	54,26	30,00	36,81	36,54
2001	51,27	63,59	30,21	38,57	37,71
2002	55,38	74,53	30,38	40,24	38,77
2003	59,49	87,35	30,53	41,85	39,75

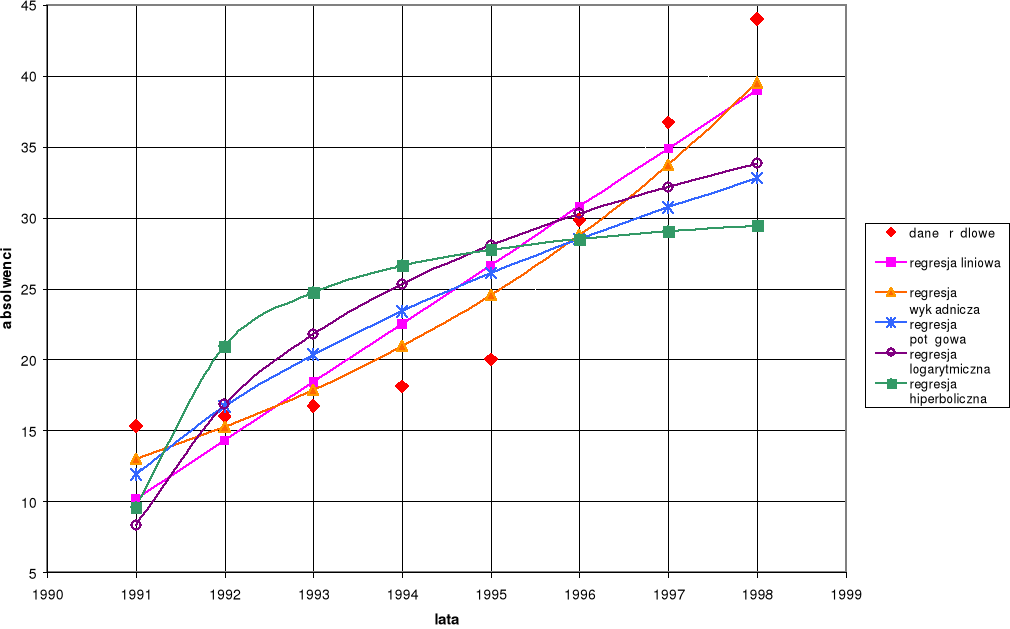
Poniżej przedstawiono wykresy obrazujące prognozy według poszczególnych modeli regresji.

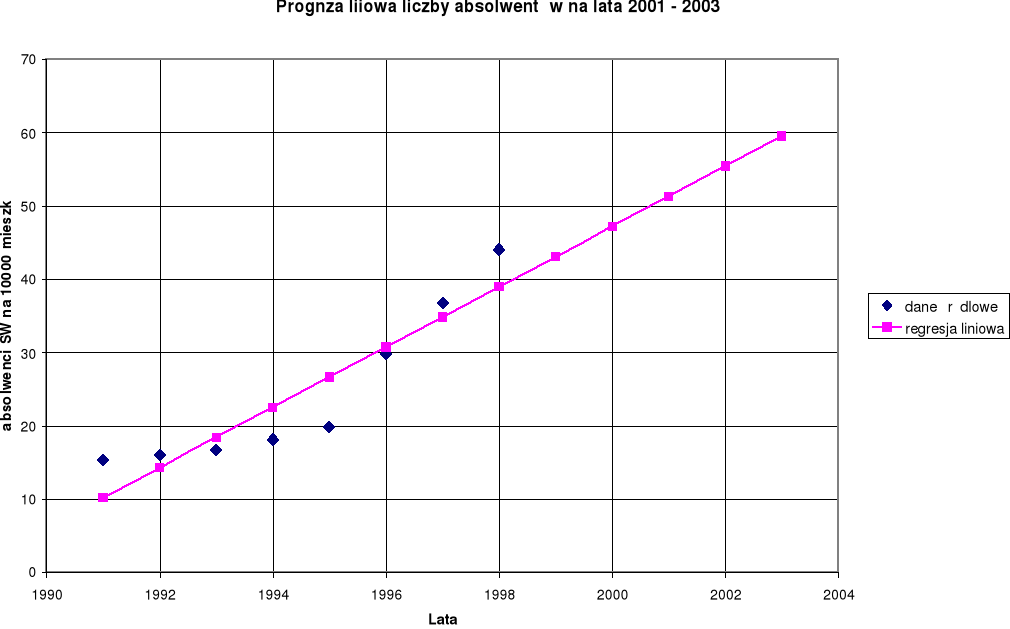
Wykres 2.

Prognozowanie liczby absolwentów szkół wyższych modelem

regresji liniowej w latach 2001 -2003.

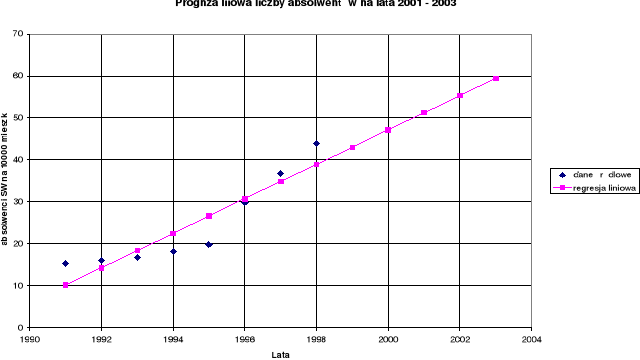
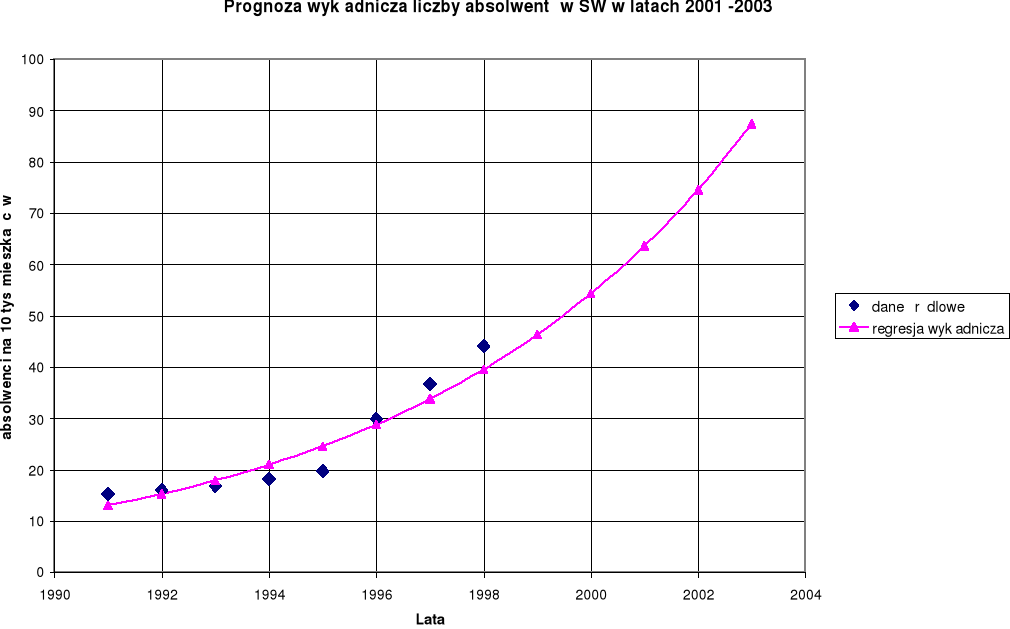
Wykres 3. Prognozowanie liczby absolwentów szkół wyższych modelem

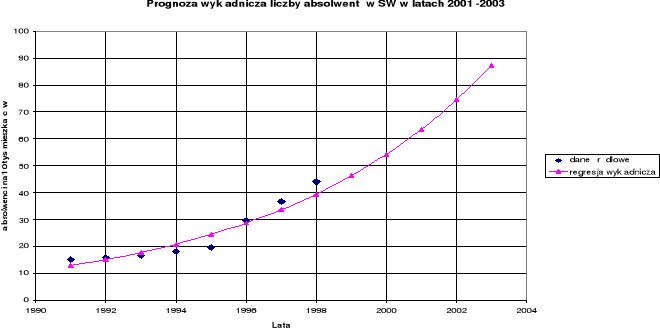
regresji wykładniczej w latach 2001 -2003.

Zarówno w modelu liniowym jak i wykładniczym prognoza liczby absolwentów wykazuje tendencję bardzo silnie wzrastającą. W rzeczywistości oznaczało by duży wzrost absolwentów szkół średnich przyjmowanych na studia. Model wykładniczy wykazuje najwyższy współczynnik korelacji R = 0,95 ozn. to że korelacja jest bardzo wysoka a zależność bardzo pewna. Według tej prognozy w roku 2003 liczba absolwentów wynosiłaby 87,35 [absol./ 10 tys. mieszk.].

Należy wziąć pod uwagę że w latach 1975 - 1979 przyrost naturalny ludności był bardzo duży (346,9 tys. do 365,2 tys.). Dla porównania w 1985 przyrost ten wynosił 296 tys. a w 1996 zaledwie 42,7 tys.[Mały Rocznik Statystyczny 1975-79 tab. „Bilans Ludności”]. Jeśli przyrost ludności w latach 1976-1979 miał tendencję wzrostową, to latach 2001 - 2003 najbardziej korzystny będzie model prognozy wykładniczej.

Prognozę tą można wybrać zarówno z punktu widzenia matematycznego, jak i inżynierskiego za najbardziej wiarygodną. Oczywiście tylko dla określonego przedziału lat. W dalszym okresie czasu liczba ta nie będzie już wzrastała jak by wynikało z wykresu. Lecz ustabilizuje się, a nawet spadnie, biorąc pod uwagę że przyrost naturalny w następnych latach gwałtownie spada.

Czynnikiem ograniczającym tak duży wzrost absolwentów szkół wyższych może stać się odpłatność za studia dzienne. Oraz limit miejsc na uczelniach wyższych.

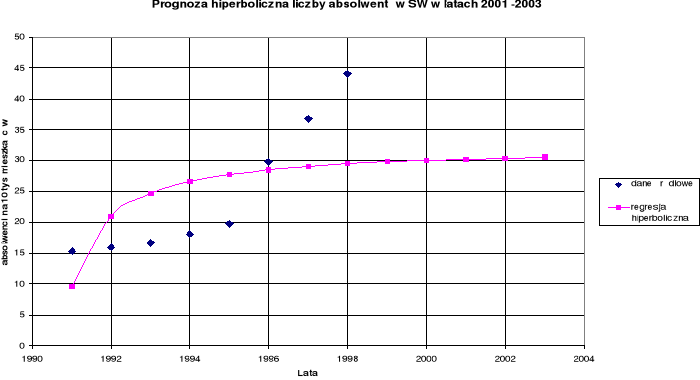
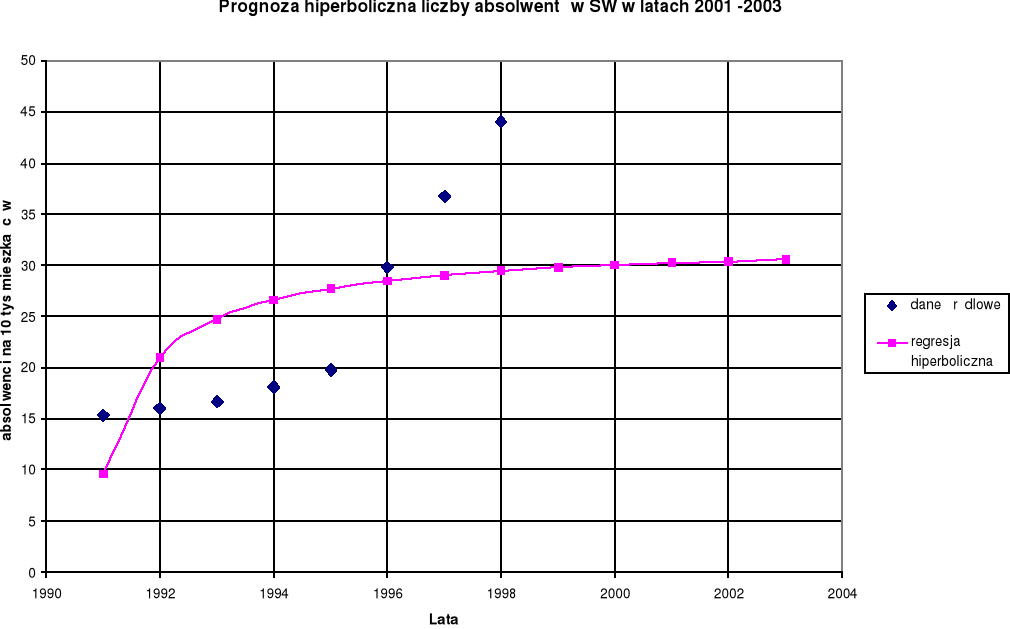
Wykres 4. Prognozowanie liczby absolwentów szkół wyższych

modelem regresji hiperbolicznej w latach 2001 -2003.

Stosując do prognozowania liczby absolwentów szkół wyższych model hiperboliczny, dochodzimy do wniosku że nie jest on adekwatny do wzrostu tej liczby, nie wykazuje tendencji wzrostowej. Jest to tzw. prognoza pesymistyczna, Prognoza ta nie odzwierciedla dynamiki wzrostu liczby absolwentów, a współczynnik korelacji jest niski R = 0,61 korelacja jest umiarkowana, zależność istotna. W rzeczywistości tak duży spadek liczby absolwentów nie jest możliwy, jedynie w wyniku jakiegoś kataklizmu.

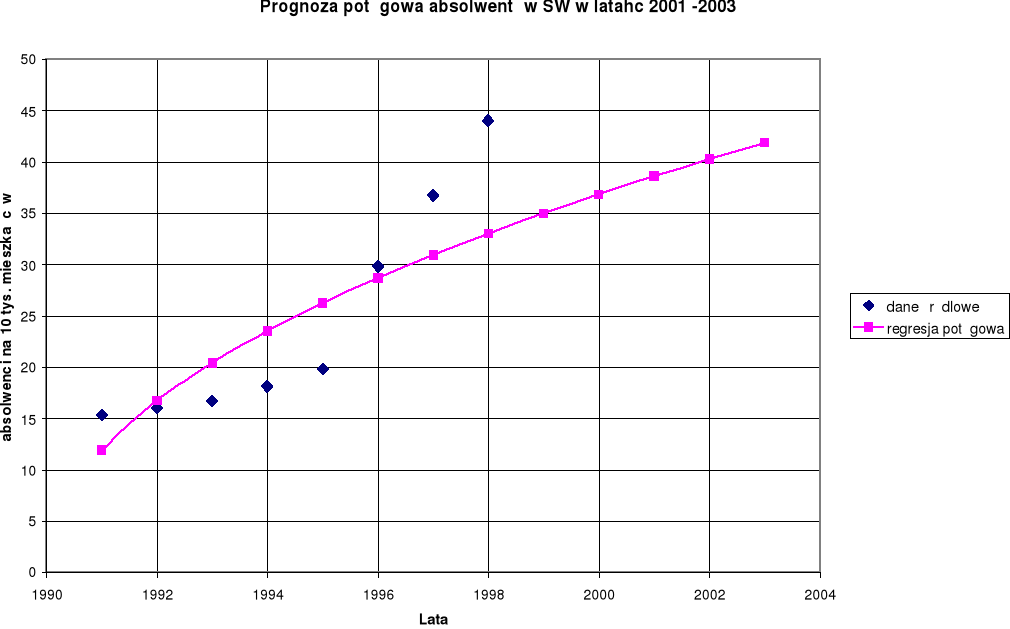
Wykres 5. Prognozowanie liczby absolwentów szkół wyższych

modelem regresji potęgowej w latach 2001 -2003

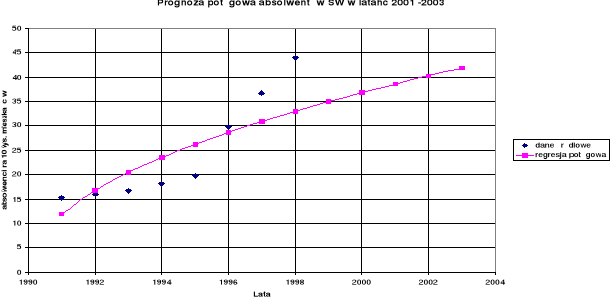
Prognozowanie za pomocą modelu regresji potęgowej możemy nazwać prognozą pesymistyczną gdyż zakłada ona że do roku 2003 liczba absolwentów szkół wyższych zmniejszy się do 41, 85 [absol./10 tys. mieszk.] Przy dzisiejszych warunkach społeczno - gospodarczych prognoza ta nie odzwierciedla tej sytuacji.

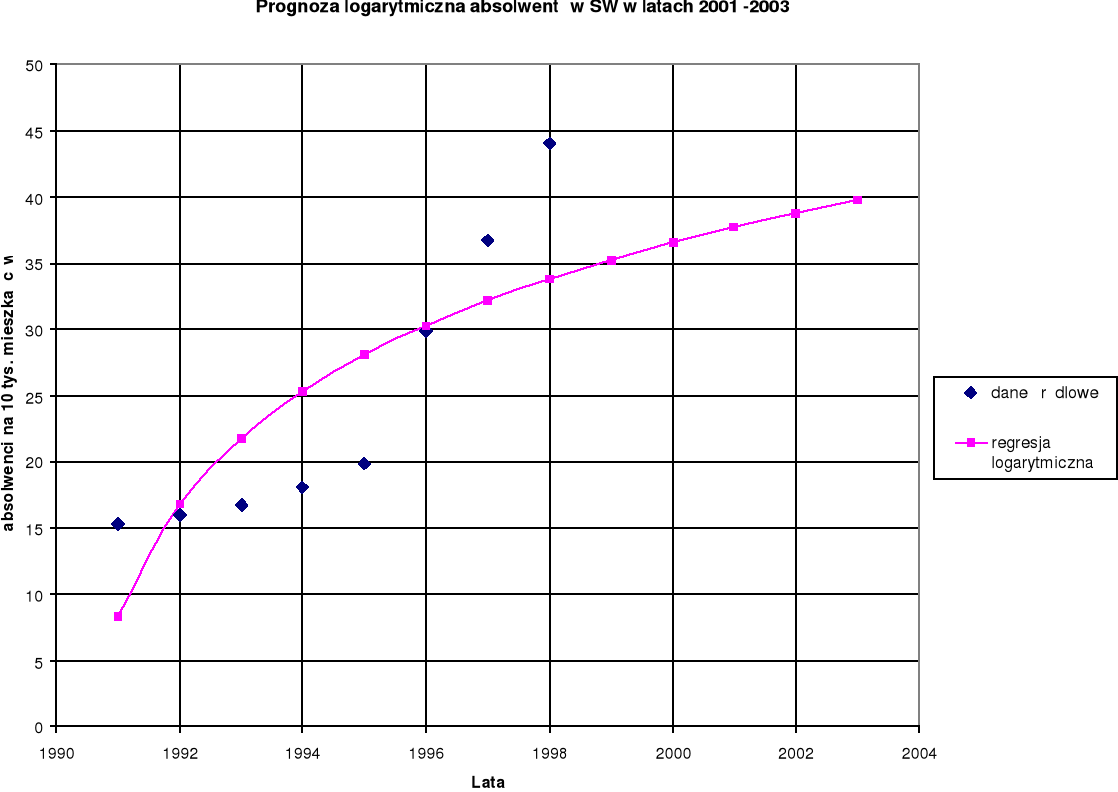
Wykres 6. Prognozowanie liczby absolwentów szkół wyższych

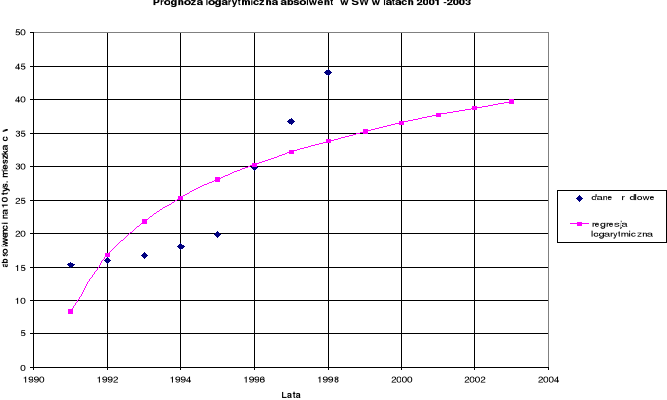
modelem regresji logarytmicznej w latach 2001 -2003.

4. Zakończenie

W projekcie przedstawiono prognozy dotyczące kształtowania się liczby absolwentów szkół wyższych w latach 2001-2003 na podstawie danych statystycznych zebranych z rocznika statystycznego z roku 1997 i 1998. Dane statystyczne obejmują lata 1991 do 1998 .

Prognozowanie przeprowadzono przy użyciu metod prognozowania statystycznego opartego na klasycznych modelach trendu. Wykorzystano modele regresji liniowej, wykładniczej, hiperbolicznej , potęgowej i logarytmicznej.

Z przeprowadzonych analiz wynika że przez najbliższe trzy lata liczba studentów będzie wzrastać, gdyż w latach 1975 - 1979 występuje większy przyrost naturalny, tym samym w latach 2001 -2003 liczba absolwentów szkół wyższych musi wzrastać. Sytuacja coraz większej konkurencji na rynku pracy zmusza młodych ludzi do podejmowania dalszej nauki w wyższych szkołach.

Wynikiem tej sytuacji będzie zwiększenie poziomu wykształcenia polskiego społeczeństwa, co będzie miało wpływ na dalszy rozwój techniki, ekonomii, przemysłu, itp.

W przypadku wprowadzenia opłat za studia dzienne liczba absolwentów może być wówczas nieco mniejsza jednak z tendencją wzrostową. Wprowadzenie odpłatności za studia dzienne nie powinno jednak obejmować studentów którzy już rozpoczęli naukę w szkołach wyższych. Wówczas nie miałoby to wpływu na absolwentów z lat 2001- 2003.

Musimy się jednak liczyć z faktem że w kolejnych latach po okresie prognozowanym liczba ta może się zmniejszyć i następnie ustabilizować na określonym poziomie.

Optymalną prognozą liczby absolwentów szkół wyższych będzie prognoza za pomocą modelu wykładniczego. Analizując matematycznie współczynnik korelacji jest największy R=0,95, zatem model ten najlepiej odzwierciedla wzrost liczby absolwentów szkół wyższych.

Przeprowadzając analizę inżynierską i uwzględniając powyższe argumenty, prognoza za pomocą modelu wykładniczego będzie odpowiadała najbardziej rzeczywistej liczbie absolwentów szkół wyższych w latach 2001-2003.

¹ Kolejny badany rok. (1991, 1992 ,1993, 1994, 1995, 1996, 1997, 1998. )

Projekt statystyczny - liczba absolwentów

8

www.wkuwanko.pl

---