Wstęp:

Drgania są rodzajem ruchu bardzo często występującym w różnego rodzaju urządzeniach technicznych. W urządzeniach mechanicznych, ze względu na tzw. niewyważenie elemen­tów obrotowych, dowolnie obrany punkt materialny tego urządzenia podlega drganiu wypadkowemu, które jest wynikiem superpozycji drgań składowych występujących najczęściej w różnych kierunkach. Ten wypadkowy ruch zależy od relacji między częstotliwościami, amplitudami oraz fazami poszczególnych drgań składowych i może być z tego względu mniej lub bardziej złożony. Gdy drgania składowe są aperiodyczne, stosunek częstotliwości drgań składowych nie daje się wyrazić liczbami całkowitymi i drgania wypadkowe nie mogą tworzyć krzywych zamkniętych, co analitycznie stanowi problem nie do roz­wiązania.

Tor punktu, który podlega wypadkowemu drganiu, tworzy krzywe za­mknięte, zwane krzywymi Lissajousa. Każda krzywa Lissajousa przebiega we­wnątrz prostokąta o bokach 2A₁ i 2A₂, gdyż jest utworzona przez nałożenie dwóch drgań harmonicznych prostopadłych do siebie. Analiza tych krzywych jest wykorzystywana w pomiarze różnicy częstotliwości drgań składowych, ró­żnicy ich faz, amplitud oraz w określaniu zmian tych wielkości w czasie.

Przykładem drgań współbieżnych niech będzie punkt drgający, który wy­konuje równocześnie dwa drgania harmoniczne proste z tą sama częstością kołową ω, lecz o różnych amplitudach A₁ i A₂ oraz fazach φ₁ φ₂

Drgania składowe będą miały postać:

Wypadkowy ruch drgający rozpatrywanego punktu będzie opisany wyra­żeniem:

Suma dwóch wektorów składowych A₁ i A₂ tworzących w chwili t=0 kąty φ₁ i φ₂ z osią x daje wektor wypadkowy A, który w tej samej chwili tworzy z osią x kąt φ. Z trójkąta OAC otrzymujemy:

oraz

Z powyższych wyrażeń można wyliczyć amplitudę wypadkową A oraz fazę φ. Wypadkowy ruch punktu jest ruchem harmonicznym prostym, opisanym równaniem:

W mechanice ruch punktu materialnego po okręgu rozpatruje się jako wynik złożenia dwóch drgań harmonicznych wzajemnie do siebie prostopad­łych

Położenie punktu P na okręgu można opisać następującymi równaniami parametrycznymi:

Po uwzględnieniu współzależności pomiędzy kątem α, a częstością kołową oraz zakładając, że R równa się amplitudzie A otrzymuje się:

Z powyższych równań wynika, że dla

ω t = 0 x = A = R, natomiast y = 0

dla

ω t = 90° x = 0, natomiast y = A = R

Po założeniu tych dwóch drgań otrzymuje się rzeczywiście równanie okrę­gu w postaci:

Gdy drgania składowe różnią się amplitudami oraz przesunięciami fazo­wymi, lecz mają te same częstotliwości, równanie wypadkowe opisuje krzywą stożkową. Gdy drgania składowe mają postaci:

wówczas korzystając z wyrażenia na cosinus sumy oraz eliminując czas z tych równań przez podstawienie

otrzymuje się końcową postać równania krzywej:

Zestawienie pomiarów i obliczenia:

Przesunięci fazowe wyznaczam z krzywych Lissajousa metodą odcinków y₀ i y_max

	1	2	3	4	5
y0	0	1	1	1	0
ymax	0	2	2	2	0
sin Θ	0	0	1	0	0
Θ	0	28	43	116	180
ΔΘ	1,0	1,8	3,2	1,8	1,0

Obliczenia dla drgań współbieżnych:

p − podstawa czasu

A − ilość amplitud

T_d = l · p T_s =

p = 0,002

A = 13

T_d = 0,01

T_s = 0,00077

ν_d = 100

ν_s = 1300

2ν_d = ν₁ − ν₂ 0,2 = ν₁ − ν

2ν_d = ν₁ +ν₂ 2,6 = ν₁ + ν₂

ν₁ = 1400 [Hz]

ν₂ = 1200 [Hz]

Rachunek błędu:

ΔΘ =

gdzie; b − wartość sin Θ

ΔA = 1

Δl = 0,4

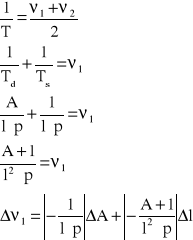
Δν₁ = 214

Δν₂ = 205

5