WYZNACZANIE MINIMALNEJ LICZEBNOŚCI PRÓBY

1. Szacowanie wartości przeciętnej

Niech cecha X ma rozkład N(m, σ).

Minimalną liczebność próby, niezbędną do oszacowania wartości przeciętnej m na poziomie ufności (1 - α), z maksymalnym błędem szacunku nie przekraczającym
obliczamy z wzoru:

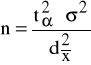
(1)

przy założeniu, że σ² jest znane i t_α otrzymujemy z tablic rozkładu normalnego, tak aby:

Jeśli σ² jest nieznane, to na podstawie wstępnej próby, liczącej n₀ elementów, przedstawionych w postaci szeregu szczegółowego, wyznacza się:

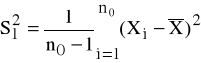
(2)

Z tablic rozkładu Studenta odczytujemy dla (n₀ - 1) stopni swobody wartość
. Wówczas:

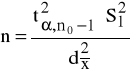
(3)

Jeśli próba będzie losowana bez zwracania, wówczas otrzymujemy następujący wzór na minimalną liczebność próby:

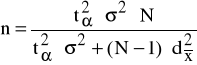
(4)

(jeśli N jest bardzo duże , w miejsce N - 1 można wstawić N)

Przykład 1.

Rozkład wagi uczniów pierwszych klas szkół podstawowych jest N(m, 3 kg). Ilu uczniów powinno się wylosować do próby, aby oszacować przeciętną wagę ucznia I klasy z maksymalnym błędem szacunku 0,5 kg na poziomie ufności (1 - α) = 0,98 ?

Rozwiązanie. Ponieważ σ jest znane, a
, więc dla
odczytujemy t_α = 2,35 i z wzoru (1) otrzymujemy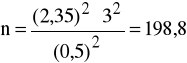
, a zatem minimalną próbą potrzebną do oszacowania średniej wagi uczniów, jest n = 199 uczniów.

Przykład 2.

Załóżmy, że rozkład wagi uczniów można ująć jako rozkład N(m, σ). Na podstawie 10-elementowej próby otrzymano
. Ilu uczniów należy wylosować do próby, aby oszacować przeciętną wagę z maksymalnym błędem 0,5 kg na poziomie ufności (1 - α) = 0,98 ?

Rozwiązanie. Korzystając z tablic rozkładu Studenta, dla 9 stopni swobody i P = 0,02 odczytujemy
i obliczamy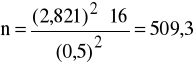
, tak więc n = 510.

Widać, że liczebność radykalnie wzrosła w stosunku do wyznaczonej w poprzednim przykładzie. Liczebność próby można ograniczyć zmniejszając dokładność szacunku. Jeśli przyjmiemy
, wówczas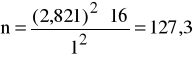
czyli n = 128.

2. Szacowanie wskaźnika struktury

Oznaczmy przez
maksymalny błąd szacunku przy szacowaniu prawdopodobieństwa sukcesu p. Niezbędną liczbę elementów n w próbie dla oszacowania p na poziomie ufności (1 - α) z maksymalnym błędem szacunku nie przekraczającym
, wyznaczamy następująco:

Jeśli rząd wielkości szacowanego prawdopodobieństwa p jest znany lub możemy go ocenić na podstawie wstępnej próby liczącej co najmniej 100 elementów, to

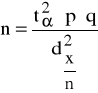
(6)

jeśli nie znamy rzędu wielkości szacowanego parametru p, wówczas zakładając wstępnie, że p = q = 0,5 , mamy:

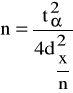
(7)

w obu wzorach t_α odczytujemy z tablic rozkładu normalnego tak, że

.

Przykład 3.

Obliczymy, jaka powinna być minimalna liczebność próby, niezbędna do oszacowania odsetka firm, które wydają na reklamę kwartalnie nie więcej niż 10 tys. zł z maksymalnym błędem szacunku równym 2%, na poziomie ufności (1 - α) = 0,99 , jeśli:

1. wstępna próba licząca 100 firm wykazała, że 30 wydaje na reklamę nie więcej niż 10 tys. zł miesięcznie.

2. nie mamy żadnych informacji o rzędzie wielkości szacowanego procentu.

Ad. a) Przyjmujemy więc p = 0,3 , q = 0,7 , a ponadto
= 0,02 oraz dla
, t_α = 2,6 . korzystając z wzoru (6) mamy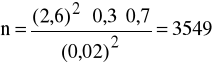
.

Ad. b) Jeśli p jest nieznane, wówczas korzystamy z wzoru (7) i otrzymujemy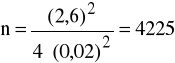
.

Widać, że brak informacji o rzędzie wielkości p powoduje, iż minimalna liczebność próby jest większa niż wówczas, gdy mamy dodatkowe informacje o p.

---