www.ise.polsl.pl/strony/czasowe/powtorka_z_chemii/analiza%20chem%20i%20rozpuszczxalnosc.doc

Reakcje w roztworach wodnych c.d.

Analiza wagowa i objętościowa

Analiza wagowa

Zasadą analizy wagowej jest wytrącenie z roztworu osadu zawierającego oznaczany składnik. Po obróbce osadu (mycie, suszenie, prażenie), znając jego wzór a więc i skład chemiczny, można wyliczyć zawartość oznaczanego składnika w próbce. Dla ułatwienia tych obliczeń stosuje się tzw. mnożniki analityczne (stechiometryczne). Poniżej przedstawiono sposób obliczania mnożnika analitycznego dla wagowego oznaczania żelaza.

Przykład 1

Wagowe oznaczanie żelaza polega najczęściej na wytrącaniu z próbki osadu wodorotlenku żelaza(III):

Osad wodorotlenku po odsączeniu oraz przemyciu praży się, w wyniku czego otrzymuje się trwały chemicznie osad tlenku żelaza(III), który po zważeniu umożliwia wyliczenie zawartości żelaza w uzyskanym trwałym osadzie. Wyliczenie zawartości żelaza (x) polega na rozwiązaniu proporcji:

2 Fe :

gdzie: m - masa zważonego osadu

x - poszukiwana masa żelaza

Fe - masa molowa żelaza 56 g/mol

- masa molowa tlenku żelaza(III) 160 g/mol

wartość ilorazu 2Fe/
nosi nazwę mnożnika analitycznego; dla tego sposobu wyliczenia ilości żelaza wynosi przykładowo 0,6994.

W trakcie wykonywania oznaczenia można korzystać z mnożników analitycznych zebranych w tablicach analitycznych, lub też wyliczać je na podstawie odpowiednich równań reakcji czy też znajomości wzorów chemicznych związków tworzących osad. Ilość składnika oznaczanego oblicza się z iloczynu mnożnika analitycznego i masy osadu. Jeżeli przykładowo w wyniku analizy wagowej na zawartość żelaza uzyskano osad tlenku żelaza(III) o masie 0,1258 g, to ilość zawartego w nim żelaza wynosi: x= 0,6994 · 0,1258 g = 0,0880 g żelaza

Znając masę analizowanej próbki, można dalej obliczyć zawartość procentową żelaza w badanym materiale lub też wykonać inne obliczenie.

Przykład 2

Ile 2-molowego roztworu amoniaku należy użyć do całkowitego wytrącenia z próbki około 0,1 g żelaza, jeżeli zaleca się stosowanie 3-krotnego nadmiaru molowego amoniaku względem żelaza.

Ilość amoniaku można wyliczyć z proporcji:

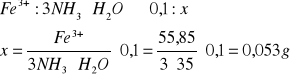
Uwzględniając trzykrotny nadmiar 3·0,053 = 0,159 g amoniaku, co po przeliczeniu na objętość 2-molowego roztworu daje:

1000
2-molowego roztworu zawiera 50 g amoniaku

x
2-molowego roztworu zawiera 0,159 g amoniaku,

x = 2,3
roztworu amoniaku

Przykład 3

Przy wykonywaniu analizy wagowej niezbędne jest określenie wielkości masy próbki analitycznej w celu otrzymania optymalnej ilości osadu. W przykładzie tym należy określić wielkość odważki rudy żelaza zawierającej około 40% żelaza, tak aby uzyskać około 0,15 g tlenku żelaza(III)

Ilość żelaza (x) w zakładanej ilości osadu wynosi:

X= 0,6994 · 0,15 g = 0,10 g żelaza

Co po uwzględnieniu zawartości procentowej żelaza pozwala obliczyć wielkość odważki rudy:

Z informacji o zawartości procentowej żelaza wynika, że:

100 g rudy zawiera 40 g żelaza

y g rudy zawiera 0,1 g żelaza,

y = 0,25 g rudy żelaza

Przykład 4

Wyprażono 0,4729 g mieszaniny węglanów wapnia i magnezu, otrzymując 0,2472 g mieszaniny odpowiednich tlenków. Wyliczyć skład procentowy mieszaniny węglanów.

Przyjmujemy następujące oznaczenia:

x - ilość gramów węglanu wapnia

y - ilość gramów węglanu magnezu

przyjęte ilości węglanów można z zastosowaniem mnożników analitycznych przeliczyć na ilości tlenków:

Przyjęte wartości umożliwiają ułożenie i rozwiązanie układu równań:

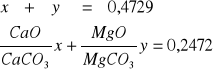
Podstawiając odpowiednie wartości mas molowych rozwiązuje się układ równań uzyskując następujące wartości: x = 0,2163 y = 0,2566

Co odpowiada 45,75% węglanu magnezu oraz 54,3% węglanu wapnia

Analiza objętościowa (miareczkowa)

Analiza miareczkowa, zwana również analizą objętościową, jest działem analizy chemicznej, której podstawą jest miareczkowanie. Oznaczanie substancji przeprowadza się na podstawie mierzenia objętości titranta, czyli roztworu mianowanego a więc posiadającego ściśle określone stężenie molowe. Analiza miareczkowa zależnie od charakteru chemicznego stosowanego titranta dzieli się następująco:

• alkacymetria (wykorzystanie reakcji zobojętniania)

• redoksymetria (wykorzystanie reakcji redox)

• kompleksometria (wykorzystanie tworzenia związków kompleksowych np. za pomocą EDTANa)

• precypitometria (wykorzystanie reakcji strącania osadu)

Dokładne stężenia titrantów, czyli roztworów do miareczkowania, ustala się za pomocą tzw. nastawiania miana na roztwory wzorcowe. W alkacymetrii do tego celu stosuje się najczęściej roztwór węglanu sodu, boraks [
] lub kwas benzoesowy. Substancje takie, specjalnie oczyszczone i osuszone odważa się w ilości stechiometrycznej i przeprowadza do roztworu w kolbie miarowej. Stężenie tak otrzymanego roztworu przyjmuje się za wzorcowe. Obecnie najczęściej stosuje się tzw. fixanale, czyli odważki analityczne sporządzone fabrycznie w zatopionych fiolkach szklanych lub pojemniczkach z tworzywa. Ilość substancji oraz jej jakość gwarantuje w tym wypadku producent fixanali np fabryka odczynników chemicznych POCH w Gliwicach. Z równania reakcji sody z kwasem solnym:

wynika, że jeden mol węglanu sodu reaguje z dwoma molami kwasu solnego. W obliczeniach, przy tego typu oznaczeniach, wygodnie jest posłużyć się stężeniem molowym. Należy jednak pamiętać, że substancje te reagują w stosunku molowym 1:2 .

Oto przykład obliczenia:

Do zmiareczkowania 20
roztworu kwasu solnego o nieznanym stężeniu zużyto 10,5
0,1-molowego roztworu węglanu sodu. 10,5
0,1-molowego roztworu węglanu sodu odpowiada więc 21
kwasu solnego o takim samym stężeniu molowym. Zawartość kwasu w próbce można obliczyć z wzoru:

Gdzie:

m - masa oznaczanego składnika

V - objętość titranta (
) - r-ru Na₂CO₃

- stężenie molowe

M - masa molowa oznaczanego składnika. Tak więc dla omawianego przykładu podstawia się następujące wartości:

Przykład 1

Odważono 1,0155 g węglanu sodu i rozpuszczono w wodzie, wprowadzono do kolby miarowej na 200
uzupełniono wodą destylowaną do nominalnej objętości. Obliczyć stężenie molowe otrzymanego roztworu. Następnie pobrano trzy równoległe próbki po 20
kwasu siarkowego(VI) o nieznanym stężeniu i miareczkowano otrzymanym wcześniej roztworem węglanu sodu. Zużyto kolejno: 20,7
, 20,6
, 20,6
roztworu mianowanego sody (węglanu sodu). Oblicz stężenie molowe roztworu kwasu siarkowego(VI) oraz jego zawartość w 1
roztworu.

Rozwiązanie:

W pierwszej kolejności oblicza się stężenie molowe roztworu mianowanego węglanu sodu, którego masa molowa wynosi 106 g

1000
roztworu 1 molowego zawiera 206 g węglanu sodu

200
roztworu 1 molowego zawiera x g węglanu sodu

x = 21,2 g węglanu sodu

200
roztworu zawierającego 21,2 g węglanu posiada stężenie 1mol/

200
roztworu zawierającego 1,0155 g węglanu posiada stężenie x moli/dm

x = 0,0479 mol/

Średnia objętość titranta z trzech równoległych pomiarów wynosi V= 20,63

Jako, że kwas siarkowy(VI) z węglanem sodu reaguje w stosunku molowym 1:1, dla obliczenia stężenia kwasu można skorzystać z następującej proporcji:

czyli 20,63·0,1=20,0·x

Stężenie molowe kwasu siarkowego(VI) jest równe 0,1

Zawartość kwasu siarkowego(VI) w badanej próbce wynosi:

Zaś w 1000
znajduje się 50 razy więcej kwasu, czyli 10,11 g kwasu siarkowego(VI)

Przykład 2

Ile należy odważyć kwasu szczawiowego
, aby otrzymać 250
0,5 molowego roztworu do zmianowania 0,05 molowego roztworu manganianu(VII) potasu.

W reakcjach redoks wygodne jest przeliczanie uwzględniające ilości wymienionych w reakcji redoks elektronów. I tak w powyższym równaniu masa odpowiadająca połowie masy molowej kwasu szczawiowego reaguje z piątą częścią masy molowej manganianu(VII) potasu (bowiem mol manganianu(VII) potasu oddaje pięć elektronów). Ta ilość manganianu przereaguje zaś z ilością kwasu szczawiowego równą połowie masy molowej kwasu szczawiowego (mol kwasu szczawiowego wymienia dwa elektrony). Tak więc dla przygotowania 250
roztworu o stężeniu 0,05 molowego kwasu szczawiowego potrzeba

Przykładowe zadania

Grawimetria (Analiza wagowa)

1/ Wyliczyć mnożniki analityczne dla analiz wagowych umożliwiających przeliczenie masy osadu na wybrany składnik:

• Al z masy
  

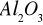
• S z masy
  

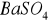
• Ca z masy
  

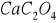
• P z masy
  

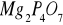
2/ Wyliczyć zawartość procentową cynku w odważkach rud, jeżeli uzyskano następujące ilości siarczku i pirofosforanu cynku:

1. z 0,7856 g rudy otrzymano 0,1176 g ZnS

2. z 0,9786 g rudy otrzymano 0,1238 g ZnS

3. z 0,1118 g rudy otrzymano 0,1118 g
   

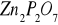
4. z 0,4916 g rudy otrzymano 0,5201 g
   

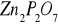
3/ Próbkę stałą poddano analizie na zawartość wody, substancji nierozpuszczalnych w wodzie oraz jonów siarczanowych. Jako kation zidentyfikowano jedynie jon sodu. Obliczyć skład procentowy badanej substancji

• 0,9823 g próbki: 0,0937 g ubytku masy po osuszeniu; 0,1107 g części nierozpuszczalnych; 0,1883 g osadu siarczanu(VI) baru

• 1,0739 g próbki; 0,0883 g ubytek masy po osuszeniu; 0,1226 g części nierozpuszczalnych w wodzie; 0,1883 g siarczanu(VI) baru

4/ Oblicz wilgotność węgla brunatnego, którego próbka równa 0,9976 g w wyniku suszenia w temperaturze 105ºC zmniejszyła masę o 0,1702 g.

5/ Ile cząsteczek wody hydratacyjnej posiada uwodniony siarczan magnezu, jeżeli w wyniku osuszenia 2,7645 g tej soli, masa odważki zmalała do 1,7410 g.

Analiza objętościowa (miareczkowa)

1. Oblicz objętość 1 molowego roztworu chlorku baru, którą należy wprowadzić do roztworu w celu całkowitego wytrącenia 0,15 g jonów siarczanowych(VI)

2. Jaką objętość kwasu siarkowego(VI) o stężeniu 0,1 mol/dm³ potrzeba do zobojętnienia 4 g 20% roztworu wodorotlenku sodu.

3. Ile
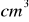
   roztworu zasady sodowej o stężeniu 1 mol/dm³ potrzeba do zobojętnienia 10 g 15% roztworu kwasu siarkowego(VI)

4. Na 20
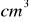
   14% roztworu kwasu siarkowego(VI) o gęstości d=1,095 g/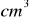
   podziałano 37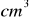
   roztworu zasady sodowej o stężeniu 2 mol/dm³. Jaki jest odczyn otrzymanej mieszaniny?

5. Odmierzono pipetą trzy próbki po 20
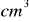
   roztworu kwasu solnego o stężeniu 0,1152 mol/dm³. Każdą próbkę miareczkowano roztworem wodorotlenku sodu zużywając kolejno: 24,70; 24,85; 24,75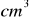
   . Obliczyć srednie stężenie molowe miareczkowanego roztworu wodorotlenku sodu.

6. Roztwór chromianu(VI) sodu jest ściśle 2 molowy. Ile
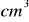
   tego roztworu należy wziąć aby otrzymać 250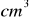
   0,1 molowego roztworu, który stosuje się w miareczkowaniu redoksowym

7. Odważono 2,9980 g technicznego wodorotlenku potasu, do jego zobojętnienia zużyto 48,4
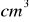
   roztworu kwasu solnego o stężeniu 0,0994 mol/dm³ . Oblicz zawartość procentową wodorotlenku potasu w produkcie technicznym.

8. Jaka jest zawartość procentowa węglanu potasu w technicznym potażu (
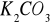
   ), jeżeli 3,5 g tego preparatu neutralizuje 42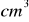
   roztworu kwasu siarkowego o stężeniu 1 mol/dm³

9. 25
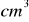
   roztworu wodorotlenku sodu o gęstości d= 1,220 g/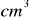
   rozcieńczono wodą destylowaną do objętości 250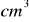
   . Dokładnie odmierzoną objętość 50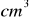
   tak otrzymanego roztworu miareczkowano 24,88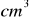
   roztworu kwasu siarkowego(VI) o stężeniu 1 mol/dm³ . Obliczyć stężenie procentowe roztworu wodorotlenku sodu przed rozcieńczeniem.

10. 25
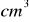
    roztworu zawierającego tlenek siarki(IV) zaabsorbowany w wodzie rozcieńczono do 250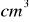
    i 10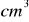
    tak otrzymanego roztworu po zakwaszeniu kwasem siarkowym zmiareczkowano 26,1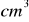
    roztworu manganianu(VII) potasu o stężeniu 0,1 mol/dm³ w przeliczeniu masy na 1 wymieniony elektron, czyli na piątą część masy molowej). Oblicz stężenie tlenku siarki (IV) w roztworze wyjściowym wyrażając je w g/dm³. Biegnąca w trakcie miareczkowania reakcja ma następujące równanie:

Zadania z zestawów maturalnych

Zad. 1/ Całkowita ilość żelaza znajdująca się w 2 g próbce rudy pochodzenia meteorytowego zastała roztworzona w kwasie. Następnie roztwór zawierający jony żelaza(II) miareczkowano roztworem manganianu(VII) potasu o stężeniu 0,1 mol/dm³ w środowisku kwasu siarkowego(VI). Do miareczkowania zużyto 27,45 cm³ roztworu manganianu(VII) potasu. Oblicz procentową zawartość żelaza w próbce rudy.

Zad. 2 / Do całkowitego strącenia bromków i chlorków zawartych w 2g mieszaniny KBr i NaCl zużyto 100 cm³wodnego roztworu azotanu(V)srebra o stężeniu 0,2 mol/dm³. Oblicz zawartość bromku potasu i chlorku sodu w mieszaninie.

Zad. 3 / Do 10 cm³ wodnego roztworu chlorku wapnia dodano nadmiar roztworu węglanu sodu, Otrzymany osad odsączono i wysuszono. Po wysuszeniu masa osadu wynosiła 2,5g. Oblicz stężenie molowe roztworu chlorku wapnia(należy założyć, że wszystkie reakcje przebiegały z wydajnością 100%)

Zad. 4 / Oblicz jaką objętość, w warunkach normalnych, zajmie wodór wydzielony w reakcji magnezu z 400 cm³ kwasu octowego o stężeniu 0,2 mol/dm³ . Należy przyjąć, że reakcje przebiegają z 100% wydajnością. Oblicz, ilość cząsteczek wodoru jaka znajduje się w otrzymanej objętości wodoru.

Zad. 5 / Po dodaniu nadmiaru kwasu octowego do 10 cm³ roztworu węglanu sodu wydzieliło się 0,224 dm³ tlenku węgla(IV). Zapisz równanie reakcji i oblicz stężenie molowe roztworu węglanu sodu.

Zad. 6 / Jaka objętość 0,1 molowego roztworu azotanu(V) srebra(I) jest niezbędna do całkowitego wytrącenia w postaci osadu AgCl jonów chlorkowych z 50 cm³ 0,2-molowego roztworu chlorku glinu?

Zad. 7 /W oparciu o bilans elektronowy w poniższym równaniu reakcji:

Wskaż utleniacz i reduktor. Oblicz jaką objętość roztworu manganianu(VII) potasu o stężeniu 0,5 mol/dm³ należy użyć, aby w reakcji z acetylenem powstało 8,3 g szczawianu dipotasu.

Zad. 8 / Do 150 g 30% roztworu węglanu sodu dodano 100 cm³ 2-molowego roztworu chlorku wapnia. Wytrącony osad przesączono i przemyto wodą. Następnie na wytrącony osad podziałano kwasem solnym w nadmiarze. Napisz równania reakcji i oblicz, jaką objętość zajął wydzielony gaz w 303 K i pod ciśnieniem 1025 hPa , jeżeli wiadomo, że straty w drugiej reakcji wynosiły 10%.

Zad. 9 / Jon fosforanowy(V) można wytrącić z roztworu w postaci osadu np.
Związek ten powstaje w reakcji rozpuszczalnego fosforanu(V) z chlorkiem magnezu i chlorkiem amonu. Napisz równanie reakcji opisanej w tekście, oblicz stężenie molowe jonów fosforanowych(V), jeżeli masa osadu wytrąconego z 50 cm³ roztworu wynosi 0,0685 g.

Zad. 10 / Zdolność łatwego utleniania jonów żelaza(II) do jonów żelaza(III) znalazła praktyczne zastosowanie przy ilościowym oznaczaniu zawartości związków żelaza(II) w próbkach. Do 10 cm³ roztworu siarczanu(VI) żelaza(II) zakwaszonego kwasem siarkowym(VI) wprowadzono kroplami roztwór manganianu(VII) potasu, który ulegał odbarwianiu. W opisanym doświadczeniu użyto 25 cm³ 0,1-molowego roztworu manganianu(VII) potasu. Oblicz stężenie molowe analizowanego roztworu siarczanu(VI)żelaza(II)

Zad. 11 / Oblicz jaka objętość 0,1-molowego roztworu dichromianu(VI) potasu przereagowała z roztworem zawierającym 5,678 g siarczanu(IV) sodu.

Zad. 12 / Do zobojętnienia 20,0 cm³ 0,2-molowego roztworu kwasu solnego zużyto 18,5 cm³ roztworu zasady barowej, a do zobojętnienia 25,0 cm³ kwasu octowego zużyto 22,4 cm³ tej samej zasady barowej. Napisz równania zachodzących reakcji w formie cząsteczkowej i jonowej. Oblicz stężenie molowe kwasu octowego.

Zad. 13 / Przez 400 g roztworu bromu w wodzie przepuszczono 1,4 dm³ propenu (warunki normalne). Po przepuszczeniu tej ilości propenu roztwór uległ całkowitemu odbarwieniu. Oblicz stężenie procentowe i molowe wody bromowej, jeżeli jej gęstość d=1,08 g/cm³ . Należy założyć, że reakcje przebiegają z wydajnością 100%.

Zad. 14 / Oblicz ile cm³ 2 molowego roztworu NaOH potrzeba do zobojętnienia 50 cm³ 1-molowego roztworu kwasu octowego.

Zad. 15 / 3,06 g mieszaniny octanu sodu i siarczanu(VI) sodu rozpuszczono w wodzie destylowanej. Do otrzymanego roztworu dodano wodny roztwór chlorku baru do całkowitego strącenia osadu. Następnie wytrącony osad przemyto, odsączono i zważono. Jego masa wynosiła 2,33 g. Oblicz jaki procent masy wyjściowej mieszaniny stanowił sód.

Zad. 16 / 5,12 g kredy szkolnej przereagowało z 60 cm³ kwasu solnego o stężeniu 2 mole/dm³. Oblicz zawartość procentową CaO i CaCO₃ w kredzie.

Zad. 17 / W celu oznaczenia zawartości amoniaku w zanieczyszczonej soli amonowej rozpuszczono 1 g tej soli w wodzie i dodano wodorotlenku sodu. Wydzielony amoniak pochłonięto w 50 cm³ roztworu kwasu solnego o stężeniu 0,5 mol/dm³ . Nadmiar kwasu odmiareczkowano, zużywając 4,25 cm³ roztworu zasady sodowej o stężeniu 0,5 mol/dm³. Oblicz procentową zawartość amoniaku w analizowanej soli amonowej.

Zad. 18 / Pomarańczowo zabarwione w roztworze jony dichromianowe(VI) utleniają 2 - propanol do acetonu, redukując się do zabarwionych na zielono kationów. Oblicz objętość 5% roztworu dichromianu(VI) potasu o gęstości 1,1 g/cm³, który przereaguje z 3 g 2 - propanolu w środowisku kwaśnym.

Zad. 19 / Stężenie jonów octanowych CH₃COO^- w roztworze kwasu octowego można oznaczyć, miareczkując roztwór kwasu roztworem zasady sodowej wobec wskaźnika. Oblicz stężenie molowe jonów octanowych w roztworze kwasu octowego, jeżeli zmiana zabarwienia wskaźnika nastąpiła po dodaniu do 0,1 dm³ roztworu kwasu 5 cm³ 0,02-molowego roztworu zasady sodowej.

Rozwiązania zadań

Rozwiązania zadań przykładowych

Zad 1. Dotyczy obliczania tzw. mnożników analitycznych, czyli współczynników umożliwiających wyliczenie ilości interesującego składnika z masy osadu, w którym się znajduje np. po wytrąceniu z analizowanego roztworu. Wzór chemiczny osadu stanowi podstawę wyliczenia takiego współczynnika. Zapis Al z Al₂O₃ oznacza, że metoda wagowego oznaczania glinu polega na ilościowym wydzieleniu osadu Al(OH)₃ , który następnie, przez prażenie, przeprowadza się w trwały osad tlenku glinu. Ze znajomości masy oraz wzoru osadu można wyliczyć masę zawartego w nim glinu.

Przykład: Al z masy Al₂O₃

Obliczmy masy molowe: M_Al=27g/mol; M_Tlenku=2x27g + 3x16g=48g

2 mole czyli 54 g Al znajdują się w 1 molu Al₂O₃ czyli 102 g tlenku

x g Al znajduje się w m g osadu tlenku

x_{gAl =} 0,5294·

Mnożnik analityczny dla obliczenia ilości glinu z masy osadu tlenku glinu wynosi x = 0,5294

Uwaga: mnożnik podaje się z dokładnością do czwartego miejsca po przecinku, to znaczy z dokładnością ważenia osadu na wadze analitycznej.

Mnożniki dla pozostałych przykładów wynoszą:

• siarka z masy BaSO₄ x =
  

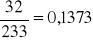
• wapnia z masy Ca₂C₂O₄ x =
  

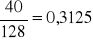
• fosforu z masy Mg₂P₄O₇
  

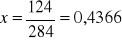
Zad. 2 W pierwszej kolejności obliczamy mnożniki analityczne dla :Zn → ZnS(1) oraz Zn →Zn₂P₂O₇ (2)

1. m _Zn = 0,1176⋅0,6701 = 0,0788g c_pZn=
% = 10% Zn

2. m_Zn = 0,0829 g

3. m_Zn = 0,0478 g
Zn

4. m_Zn = 0,2224 g
Zn

Zad.3

Przykład 1

m_próbki =0,9823 g m_wody= 0,1107 g m _nierozp= 0,1107 g

Jako, że jedynym stwierdzonym jonem jest jon sodu należy sądzić, że solą jest siarczan(VI) sodu, którego ilość wyliczymy, wytrącony osad to siarczan(VI) baru.

Z 1 mola Na₂SO₄ powstaje 1 mol BaSO₄, uwzględniając masy molowe można powiedzieć, że:

142 g Na₂SO₄ w wyniku reakcji daje 233 g BaSO₄ x g Na₂SO₄ w wyniku reakcji daje 0,1883 g BaSO₄

Obliczenie składu procentowego:

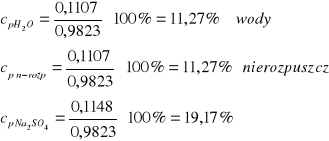
Przykład 2

Zad.4

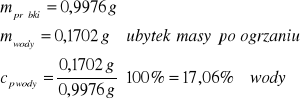
Zad.5

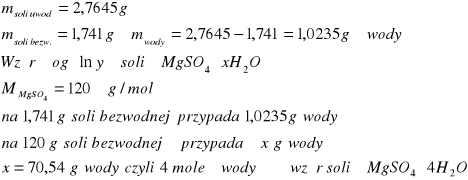
Analiza objętościowa

Zad.1

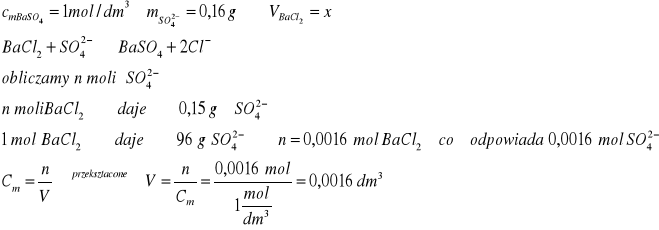
Do wytrącenia 0,15 gramów jonów siarczanowych(VI) potrzeba 1,6 cm³ 1 molowego roztwory BaCl₂

Zad.2

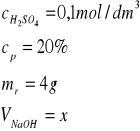
H₂SO₄ +2NaOH→Na₂SO₄ + 2H₂O

Ilość wodorotlenku sodu w 4 g 20% wynosi m_NaOH = 0,8 g

Z równania reakcji obliczmy niezbędną do zobojętnienia tej ilości wodorotlenku ilość moli kwasu siarkowego(VI)

1 mol H₂SO₄ zobojętnia 2 mole NaOH czyli 80 g NaOH

n moli H₂SO₄ zobojętnia 0,8 g NaOH

n = 0,01 mol H₂SO₄

z wzoru na stężenie molowe c_m = n/V obliczamy objętość V=n/c_m=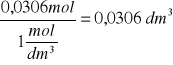

Zad.3

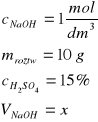
Równanie przebiegającej reakcji: H₂SO₄ +2NaOH→Na₂SO₄ + 2H₂O

Obliczmy ilość kwasu siarkowego(VI) w 10g 15% roztworu m_kwasu= 1,5 g kwasu. Jako, że ilość NaOH podana jest w postaci stężenia molowego, również ilość zasady wyrazimy w molach: Na podstawie równania reakcji:

1 mol kwasu czyli 98 g H₂SO₄ reaguje z 2 molami NaOH

1,5 g H₂SO₄ reaguje z x molami NaOH x=0,0306

Z wzoru na stężenie molowe: c_m=x/V ⇒ V=x/c_m V=0,0306/1=0,0306 dm³

Odpowiedź: Do zobojętnienia roztworu kwasu potrzeba 30,6 cm³ roztworu NaOH

Zad.4

Roztwór kwasu: V=2 cm³ c_p=14% d=1,095 g/cm³

Roztwór zasady: V=37 cm³ c_m=2 mol/dm³

Obliczenia na podstawie biegnącej, według następującego równania, reakcji:

H₂SO₄ +2NaOH→Na₂SO₄ + 2H₂O

Z równania wynika, że kwas reaguje z zasadą w stosunku molowym 1:2

Obliczamy ilości moli:

Kwasu siarkowego(VI): m_kwasu = 2 cm³⋅ 1,095 g/cm³⋅0,14 =0,307 g

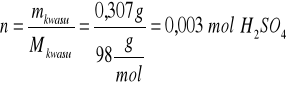
Zasady sodowej:

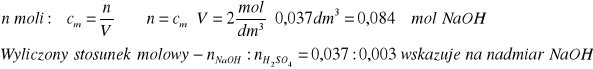
Roztwór po reakcji będzie więc miał odczyn zasadowy (pH>7)

Zad.5

V_HCl = 20 cm³ ; c_HCl = 0,1152 mol/dm³; V_NaOH po uśrednieniu trzech wyników: 24,77 cm³ Obliczyć stężenie molowe roztworu NaOH c_NaOH

Z równania reakcji: NaOH + HCl = NaCl + H₂O wynika, że kwas solny reaguje z zasadą sodową w stosunku molowym 1:1, czyli n_NaOH = n_HCl a z tego wynika, że: V_NaOH⋅c_NaOH=V_HCl⋅c_HCl

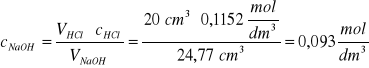
Zad. 6

c₁= 2 mol/dm³

V₁ = x cm³

c₂ = 0,1 mol/dm³

V₂ =200 cm³

Ilość substancji rozpuszczonej nie uległa zmianie, więc w roztworze znajduje się ta sama ilość moli substancji rozpuszczonej, czyli:

n₁= n₂ => V₁⋅c₁ = V₂⋅c₂

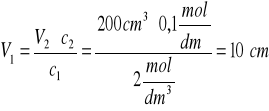
Należy rozcieńczyć 10 cm³ roztworu o stężeniu 2mol/dm³

Zad.7

m_NaOH = 2,9980 g

V_HCl = 48,4 cm³

C_HCl = 0,0994 mol/dm³

C_{p NaOH} = x

Sytuację opisaną w zadaniu przedstawia równanie: NaOH + HCl = NaCl + H₂O

zasada sodowa z kwasem solnym reaguje w stosunku molowym 1:1 tak więc:

n_NaOH=n_HCl →

1 mol NaOH - 40 g NaOH

0,0048 mol NaOH - x g NaOH

x = 0,1924 g NaOH

Obliczenie zawartości procentowej NaOH w produkcie technicznym:

2,998 g technicznego NaOH - 100%

0,1924 g NaOH - x%

x% = 6,42 % NaOH

Zawartość NaOH w produkcie technicznym wynosi 6,42%

Zad. 8

m = 8,5g technicznego K₂CO₃

V_kwasu = 42 cm³ = 0,042 dm³

C_kwasu = 1 mol/dm³

Sytuację zadania opisuje równanie reakcji:

K₂CO₃ + H₂SO₄ = K₂SO₄ + H₂O + CO₂(↑)

Obliczamy masę węglanu potasu, która przereagowała z kwasem siarkowym(VI)

n_kwasu= 0,042 dm³∙1 mol/dm³=0,042 mol H₂SO₄

Z równania reakcji wynika, że 1 mol węglanu, czyli 138 g reagują z 1 mol kwasu

X g reagują z 0,042 mol kwasu

X = 5,796 g węglanu potasu; obliczamy zawartość procentową:

8,5 g technicznego odpowiada 100%

5,796 g węglanu odpowiada x%

x = 68,19 % K₂CO₃

Zad. 9

V_NaOH = 25 cm³; d = 1,22 g/cm³; V₁= 250 cm³; V₂= 50 cm³; V_kwasu=24,88 cm³; c_m= x mol/dm³

Równanie reakcji: H₂SO₄ + 2NaOH = Na₂SO₄ + 2H₂O

Obliczmy objętość roztworu kwasu, niezbędną do zobojętnienia całego roztworu zasady:

50 cm³ zasady trzeba 0,248 dm³ kwasu

250 cm³zasady potrzeba x dm³ kwasu, czyli V_kwasu= 0,124 dm³

Z objętości i stężenia roztworu kwasu obliczamy ilość moli kwasu siarkowego(VI)

n = 0,124 dm³∙ 1 mol/dm³ = 0,124 mola kwasu siarkowego, na podstawie równania reakcji obliczymy masę wodorotlenku sodu (m_NaOH)

2 mole NaOH czyli 80 g NaOH reaguje z 1 molem kwasu siarkowego(VI)

x g NaOH reaguje z 0,124 molami kwasu

m_NaOH = 9,92 g NaOH

Obliczamy masę wyjściową roztworu: m_r =V[cm³]∙d[g/cm³] = 25 cm³∙1,220 g/cm³ = 30,5 g

Na podstawie wyliczonych wielkości możemy wyliczyć stężenie procentowe roztworu:

30,5 g roztworu stanowi 100%

9,42 g wodorotlenku sodu stanowi c_p roztworu

c_p = 32,5%

Zad. 10

W reakcjach można stosować wygodne przeliczenie ilości substnacji przypadającej na jeden wymieniony w reakcji redoks elektron (mol elektronów):

n =V ∙ c_m= 0,0261∙0,1 = 0,00261

Podobnie wyliczamy ilość tlenku siarki(IV) przypadająca na 1 mol elektronów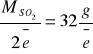

Z równania reakcji redoks wynika więc, że 32 g SO₂ przypada na 0,4 mol/e KMnO₄

x g SO₂ przypada na 0,0026 mol/e KMnO₄

x = 0,21 g SO₂

Uwzględniając rozcieńczenie całkowita ilość tlenku siarki(IV) wynosi m = 25∙0,21 g SO₂ = 5,22 g SO₂

Zadania z zestawów maturalnych - rozwiązania

Zad. 1

m_rudy = 2 g

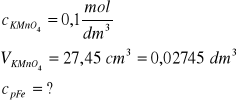
W trakcie miareczkowania biegnie następująca reakcja redoks:

Z informacji o roztworze manganianu(VII) potasu obliczymy ilość moli tego związku, która jest równa ilości moli jonów manganowych(VII):

Z równania reakcji obliczmy masę żelaza, które weszło w reakcję:

5 moli żelaza czyli 280 g reaguje z 1 molem KMnO₄

m_Fe reaguje z 0,002745 mol KMnO₄

m_Fe = 0,77 g Fe

Obliczamy zawartość procentową żelaza w rudzie:

2 g rudy stanowią 100%

0,77 g Fe stanowi x% x = 38,5% Fe

Zad. 2

m_mieszaniny = 2g

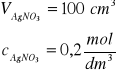
do obliczenia skład procentowy mieszaniny soli

Równania reakcji:

KBr + AgNO₃ =KNO₃ + AgBr(↓)

NaCl + AgNO₃ = NaNO₃ +AgCl(↓)

Na podstawie powyższych równań reakcji można ułożyć układ równań matematycznych z dwiema niewiadomymi, które będą odpowiednio oznaczały x ilość moli KBr oraz y ilość moli NaCl, po uwzględnieniu mas molowych można oznaczyć masy składników w formie ilorazu ilości moli i mas molowych: M_KBr = 119g/mol; M_NaCl = 58g/mol

Suma ilości moli ( x + y) bromku potasu i chlorku sodu będzie równa ilości moli azotanu(V) srebra użytego do strącenia osadu czyli n = c ∙V[dm³] = 0,02 mol

Układ równań:

Suma mas 119 x + 58 y = 2

Suma moli x + y = 0,02

Wyliczone wartości niewiadomych wynoszą odpowiednio: x = 0,014; y = 0,006

Masy odpowiednich soli wynoszą:

m_KBr = 119g/mol∙0,014 = 1,72 g;

m_NaCl = 58 g/mol∙0,006 = 0,35 g

Uwaga: Suma mas nieco przewyższa podaną wartość, wynika to z przyjętej dokładności obliczeń i zastosowanych zaokrągleń.

Zad. 3

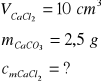
Równanie reakcji opisanej w zadaniu:

CaCl₂ + Na₂CO₃ = CaCO₃(↓) + 2 NaCl

Jako, że w zadaniu chodzi o wyliczenie stężenia molowego, ilość chlorku wapnia wyrazimy w molach.

1 mol CaCl₂ da w wyniku reakcji 1 mol CaCO₃ czyli 100 g (M_{węglanu wapnia)} = 100 g/mol

x moli CaCl₂ do w wyniku reakcji 2,5 g CaCO₃

x = 0,025 mola CaCl₂

Obliczamy stężenie molowe roztworu chlorku wapnia:

Zad. 4

V_kw = 400 cm³ = 0,4 dm³

c_{m kw} = 0,2 mol/dm³

n - ilość cząsteczek wodoru

Równanie zachodzącej reakcji: Mg + 2CH₃COOH = Mg(CH₃COO)₂ + H₂(↑)

Obliczmy ilość moli kwasu octowego:

Korzystając z równania reakcji układamy proporcję:

2 mole kwasu dają 22,4 dm³ wodoru

0,08 mola kwas daje x dm³ wodoru

x = 0,896 dm³ wodoru

Do obliczenia ilości cząsteczek skorzystamy z mola jako miary liczności substancji:

1 mol czyli 22,4 dm³ wodoru to 6,03∙10²³ cząsteczek wodoru(liczba Avogadra)

0,896 dm³ wodoru zawiera x cząsteczek wodoru

x = 0,24∙10²³ cząsteczek wodoru

Zad. 5

V_r =10 cm³

= 0,224 dm³

= ?

Równanie reakcji: Na₂CO₃ + 2CH₃COOH → 2CH₃COONa + H₂O + CO₂

Obliczamy ilość moli węglanu sodu niezbędną do otrzymania 0,224 dm³ CO₂

Z równania reakcji wynika, że 1 mol Na₂CO₃ daje 22,4 dm³CO₂ n mol Na₂CO₃ daje 0,224 dm³CO₂

n = 0,01 mol

Obliczamy stężenie molowe roztworu:

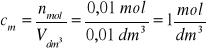
Zad. 6

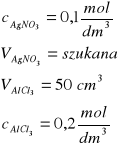
Równanie reakcji: AlCl₃ +3AgNO₃ =3AgCl + Al(NO₃)₃

Obliczamy ilość moli AlCl₃ n = V∙c = 0,05 dm³∙0,2
=0,01 mol AlCl₃

Z równania reakcji obliczamy ilość moli AgNO₃

1 mol AlCl₃ reaguje z 3 molami AgNO₃

0,01 mola AlCl₃ reaguje z 0,03 molami AgNO₃

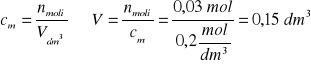
Zad. 7

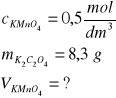
Z równania reakcji: 2KMnO₄+5K₂C₂O₄+8H₂SO₄=6K₂SO₄+2MnSO₄+10CO₂+8H₂O wynika że:

2 mole KMnO₄ reagują z 5 molami szczawianu, czyli 830 g

n moli KMnO₄ reaguje z 8,3 g

n = 0,02 mola KMnO₄

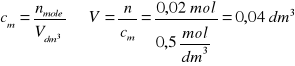
Zad. 8

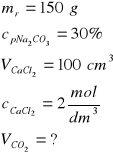
Równanie reakcji: Na₂CO₃ +CaCl₂ = 2NaCl + CaCO₃(↓)

Obliczamy masy substratów reakcji:

a/ masa węglanu sodu 150g roztworu to 100%

x g węglanu to 30% x = 45 g

b/ masa chlorku wapnia

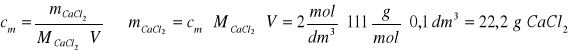
W celu ustalenie, który z substratów był wzięty w nadmiarze, z równania reakcji obliczamy ilości węglanu wapnia przy użyciu każdego z substratów. Właściwy będzie wynik mniejszy, gdyż wyższy odpowiada ilości substratu wziętego w nadmiarze

1 mol Na₂CO₃ czyli 106 g daje 1 mol CaCO₃ czyli 100 g

45 g daje x₁ g x₁ = 42,5 g CaCO₃

1 mol CaCl₂ czyli 111 g daje 1 mol CaCO₃ czyli 100g

22,2 g daje x₂ g x₂= 20 g CaCO₃

Otrzymano więc 20 g węglanu wapnia (decyduje o tym ilość wziętego z niedomiarem chlorku wapnia). Objętość wydzielonego CO₂ (warunki normalne)

Z 1 mola CaCO₃ czyli z 100g powstaje 1 mol CO₂ czyli 22,4 dm³

z 20g powstaje x dm³

Wyliczona objętość, w warunkach normalnych, wynosi 4,48 dm³, przeliczamy ją na warunki opisane w zadaniu zgodnie z równaniem:

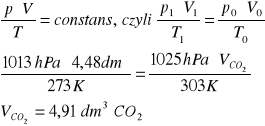
Zad. 9

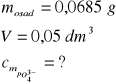
Równanie reakcji: Na₃PO₄+MgCl₂+NH₄Cl → NH₄MgPO₄ +3NaCl

1 mol
daje mol osadu, czyli 137 g osadu

x moli daje 0,0685 g osadu x=0,005 mol

Obliczamy stężenie molowe:

Zad. 10

Zad. 11

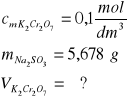
Równanie przebiegającej reakcji:

3Na₂SO₃ + K₂Cr₂O₇ + 4H₂SO₄ → Cr₂(SO₄)₃ + 3Na₂SO₄ + K₂SO₄ +4H₂O

3 mole Na₂SO₃ czyli 318g reaguje z 1 molem K₂Cr₂O₇

5,6 g reaguje z x molami; x=0,018mol K₂Cr₂O₇

Objętość roztworu dichromianu(VI) będzie wynosiła:

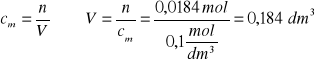
Zad 12.

V_HCl = 20 cm³

c_HCl = 0,2 mol/dm³

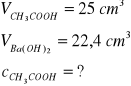
Ba(OH)₂ + 2HCl → BaCl₂ + 2H₂O;

Ba(OH)₂ + 2CH₃COOH →Ba(CH₃COO)₂ + 2H₂O

Obliczamy stężenie molowe Ba(OH)₂

n_HCl = 0,02 dm³∙0,2 mol/dm³ = 0,0004mol HCl ≡ 0,0002 mole Ba(OH)₂

więc ilość moli kwasu octowego dwukrotnie większa, czyli n = 0,000448; ilość ta znajdowała się w 25 cm³ roztworu, czyli stężenie tego roztworu wyniesie:

Zad. 13

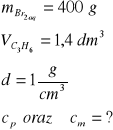
Równanie reakcji: C₃H₆ + Br₂ = C₃H₆Br₂

Na podstawie równania reakcji obliczymy masę bromu w roztworze:

1 mol czyli 22,4 dm³ C₃H₆ reaguje z 1 molem czyli 160 g Br₂

1,4 dm³ C₃H₆ reaguje z x g Br₂

x = 10 g Br₂

Obliczamy stężenie procentowe: 400 g roztworu odpowiada 100%

10g Br₂ odpowiada c_p= 2,5%

Obliczamy stężenie molowe:

Jako, że gęstość roztworu d = 1g/cm³; objętość V = 0,4 dm³; M_bromu = 160 g/mol

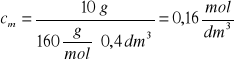
Zad. 14

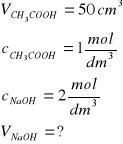
Z równania reakcji: NaOH + CH₃COOH = CH₃COONa + H₂O wynika, że:

Kwas reaguje z zasadą w stosunku molowym 1:1, tak więc:

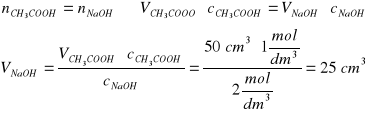
Zad. 15

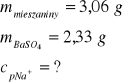
Z równania reakcji obliczamy ilość siarczanu(VI) sodu

Na₂SO₄+ BaCl₂ → BaSO₄(↓) + 2NaCl

1 mol czyli 142 g Na₂SO₄ dają 1 mol czyli 233 g BaSO₄

x g Na₂SO₄ dają 2,33 g BaSO₄

x = 1,42 g Na₂SO₄

Mieszanina składa się więc z 1,42 g siarczanu(VI) sodu oraz (3,06g - 1,42g) 1,64 g octanu sodu.

Obliczamy ilość sodu w składnikach mieszaniny:

1 mol siarczanu(VI) sodu czyli 142 g zawiera 46 g sodu

1,42 g zawiera 0,46 g sodu

1 mol octanu sodu czyli 82 g zawierają 23 g sodu

1,64 g zawiera x g sodu; x = 0,46 g Na

Łączna ilość jonów sodu m_Na= 0,92 g w 3,06 g mieszaniny

Zad. 16

m_miesz = 5,12 g

V_HCl = 60 cm³ = 0,06 dm³

C_HCl = 2 mol/dm³

C_pCaO = ?

Równania przeprowadzonych reakcji:

CaO + 2HCl = CaCl₂ + H₂O

CaCO₃ + 2HCl = CaCl₂ + H₂O + CO₂

Zakładamy, że mieszanina zawiera x moli CaO oraz y moli CaCO₃

m_CaO = x moli∙ M_CaO = 56x; m = y moli∙ M_węglanu = 100y

suma mas: 56x + 100y = 5,12

ilość moli HCl 2x + 2y = 0,06 dm³∙ 2 mol/dm³ = 0,12 mol

ostateczny układ równań: 56x + 100y = 5,12

2x + 2y = 0,12

Wynik: x = 0,02; y= 0,04 Ilość tlenku m_CaO = 56x = 1,12 g

5,12 g kredy odpowiada 100%

1,12 g CaO odpowiada c_pCaO c_pCaO = 21,9%

Zad. 17

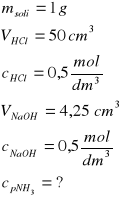
Ilość moli HCl przed pochłanianiem:

n_HCl = V[dm³]∙c[mol/dm³] = 0,05 dm³∙0,5mol/dm³ = 0,025 moli HCl

Ilość moli HCl, która przereagowała z amoniakiem (reagują w stos. mol.=1:1

n_NaOH = 0,00425 dm³∙ 0,5 mol/dm³) = 0,002 mol NaOH i tyle samo HCl

Ilość moli HCl, która przereagowała z amoniakiem

n_HCl = n_og - n_NaOH = 0,025 - 0,002 = 0,023 mole HCl

Równanie reakcji pochłaniania amoniaku:

NH₃ + HCl = NH₄Cl

1 mol amoniaku czyli 17 g NH₃ reaguje z 1 molem kwasu

x g NH₃ reaguje z 0,023 molami kwasu

x = 0,0723 g NH₃

Obliczenie zawartości procentowej: 1 g soli - 100%

0,0723 g NH₃ -

Zad. 18

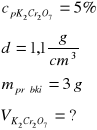
Równanie zachodzącej reakcji redoks:

3C₃H₇OH + K₂Cr₂O₇ + 4H₂SO₄ = 3C₃H₆O + K₂SO₄ + Cr₂(SO₄)₃ + 7H₂O

1 mol K₂Cr₂O₇ czyli 294 g reaguje z 3 molami C₃H₇OH czyli 162 g

x g reaguje z 3 g;

x = 5,44 g dichromianu(VI) potasu

Obliczamy masę 5% roztworu:

5,44 g K₂Cr₂O₇ stanowi 5%

m_roztw. stanowi 100%

m_roztw. = 108,9 g roztworu; V= m/d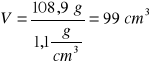

Zad. 19

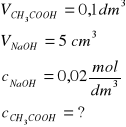
Z równania reakcji wynika, że kwas octowy reaguje z zasadą sodową w stosunku molowym 1:1, czyli można to wyrazić:

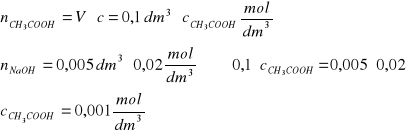
Reakcje w roztworach wodnych

Część II - Iloczyn rozpuszczalności

Wśród zadań maturalnych w zestawie roku 2005 znalazło się również takie, które wymagało od ucznia precyzyjnego określenia a właściwie rachunkowego uzasadnienia, czy w podanych warunkach nastąpi wytrącenie osadu. Chodziło w tym wypadku o przewidywanie wytrącenia osadu nie na podstawie tzw. tablicy rozpuszczalności a jedynie podanych stężeń mieszanych roztworów, czyli mówiąc inaczej znajomości tzw. iloczynu rozpuszczalności. Mimo, że uczniowie przygotowani są teoretycznie do zrozumienia tego pojęcia gdyż dosyć szczegółowo mówi się o reakcjach nieodwracalnych i warunkach ich przebiegu, o prawie działania mas i regule przekory iloczyn rozpuszczalności omawia się pobieżnie lub wręcz pomija. Tak więc pozostaje jeden krok do zrozumienia pojęcia iloczynu rozpuszczalności, gdyż pojęcie to jest w pewnym sensie przybliżone już przy omawianiu pH oraz iloczynu jonowego wody. Wynika on również naturalnie z faktu, że w tabelach rozpuszczalności np. w zbiorze zadań Krzysztofa Pazdry i innych podręcznikach określa się substancji jako rozpuszczalne, nierozpuszczalne oraz słabo rozpuszczalne. W tej sytuacji rodzą się wątpliwości myślących uczniów - co to znaczy słabo rozpuszczalny ? - wytrąci się wówczas osad czy też nie ? Jak to przewidzieć ? Tak więc korzystając ze znanych pojęć stałej równowagi i reguły przekory spróbujmy przybliżyć to zagadnienie.

W każdym nasyconym roztworze trudno rozpuszczalnego elektrolitu istnieje stan równowagi pomiędzy jonami elektrolitu w roztworze a nadmiarem fazy stałej (osadem) pozostającej z nim w równowadze. Ponieważ elektrolit taki jest w wodzie trudnorozpuszczalny, zatem jego nasycony roztwór jest bardzo rozcieńczony. W takim roztworze znajdują się wyłącznie jony elektrolitu, natomiast nie są w nim obecne cząsteczki niezdysocjowane (α = 100%). Równowaga w takim układzie jest tzw. równowagą dynamiczną, to znaczy w jednostce czasu taka sama ilość cząsteczek przechodzi do roztworu i jednocześnie ulega wytrąceniu z niego. Stan równowagi pomiędzy trudno rozpuszczalnym elektrolitem a jego nasyconym roztworem odpowiada przemianie:

(KtAn)_stały ↔ Kt⁺ + An^-

osad roztwór nasycony

a wyrażenie na stałą równowagi tego procesu, zgodnie z prawem działania mas, posiada postać:

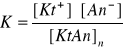
Wartość tej stałej równowagi jest niezmienna w stałej temperaturze, zgodnie z prawem działania mas. Ponieważ ilość substancji w fazie stałej, ze względu na duży nadmiar (w osadzie) jest również niezmienna w niezmiennej temperaturze, wyrażenie [KtAt]_st posiada wartość stałą. Iloczyn dwóch stałych wartości jest również stałą nazywaną iloczynem rozpuszczalności i oznaczaną najczęściej literą L.

K∙[KtAn]_st = L = [Kt⁺]∙[An^-]

Iloczyn rozp. Iloczyn jonowy

Iloczyn stężeń jonowych [Kt⁺]∙[An^-] nosi nazwę iloczynu jonowego

Iloczyn jonowy trudno rozpuszczalnego elektrolitu w roztworze nasyconym - pozostającym w równowadze z nadmiarem fazy stałej - jest równy iloczynowi rozpuszczalności, wartości stałej w stałej temperaturze.

W obliczeniach rozpuszczalności sprawą podstawową jest poprawne wstawienie wartości stężeń jonowych do wyrażeń na iloczyn rozpuszczalności odpowiednich elektrolitów. Wartości stężeń jonowych wynikają z równania dysocjacji trudno rozpuszczalnej soli. Niechaj przykładowo rozpuszczalność chlorku srebra wynosi x : [AgCl] = x. Z każdej cząsteczki AgCl powstaje 1 jon srebra i 1 jon chlorkowy, zatem [Ag⁺] = [Cl^-] Po wstawieniu stężeń do iloczynu jonowego otrzymuje się: L_AgCl = [Ag⁺]∙[Cl^-] = x∙ x = x², stad

Jeżeli stężenie [MgNH₄PO₄] = x, a każda cząsteczka dysocjuje na 1 jon magnezu, jeden jon amonowy i jeden jon ortofosforanowy(V), to ich stężenia wynoszą: [Mg²⁺] = x ; [NH₄⁺] = x ; [PO₄^3-] = x

L = [Mg²⁺]∙[NH₄⁺]∙[PO₄³⁺] = x∙x∙x =x³

Stąd

Jeżeli stężenie CaF₂ oznaczy się przez x: [CaF₂] = x, a każda cząsteczka tej soli dysocjuje na 1 jon wapnia i 2 jony fluorkowe, zatem [Ca²⁺] =x i [F^-] =2x to:

Przykładowe zadanie umożliwiające precyzyjne określenie, czy nastąpi wytrącenie osadu.

Do 500 cm³0,008 molowego roztworu chlorku wapnia dodano 500 cm³ 0,01 molowego roztworu siarczanu sodu. Wskazać, czy w podanych warunkach wytrąci się osad węglanu wapnia. Wartość iloczynu rozpuszczalności wynosi L= 2,4∙10^-5.

Rozwiązanie. Po zmieszaniu roztworów podwoi się objętość a stężenia soli zmniejszą się do połowy i wyniosą: [CaCl₂] = [Ca²⁺] = 0,008∙0,5= 0,004 mola/dm³; [Na₂SO₄] = [SO₄^2-] = 0,01∙ 0,5 = 0,005 mol/dm³

Iloczyn jonowy siarczanu(VI) wapnia jest równy:

L = [Ca²⁺]∙[SO₄^2-]=0,004∙0,005= 2,0∙10^-5

I jest mniejszy iloczynu rozpuszczalności CaSO₄ 2,0∙10^-5 < 2,4∙ 10^-5, taki roztwór jest więc nienasycony i osad nie wytrąci się.

Można również na podstawie takich obliczeń precyzyjnie określić, który z przykładowych związków jest lepiej rozpuszczalny.

Przykładowe zadanie Który elektrolit jest lepiej rozpuszczalny w wodzie: węglan kadmy czy wodorotlenek kadmu ? Wartości iloczynów rozpuszczalności wynoszą dla węglanu L = 5,2∙10^-12 zaś dla wodorotlenku L = 2,8∙10^-14 Rozpuszczalność podać w gramach na 1 dm³ roztworu nasyconego.

Rozwiązania: Wyrażenia na iloczyny rozpuszczalności związków mają postać:

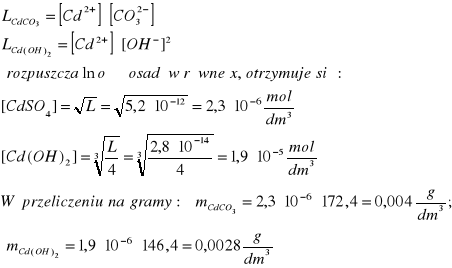
Elektrolitem lepiej rozpuszczalnym i to siedem razy jest wodorotlenek kadmu, mimo mniejszej wartości iloczynu rozpuszczalności. Wynika to z różnej postaci wyrażeń określających zależność między rozpuszczalnością i iloczynem rozpuszczalności obu tych elektrolitów.

Propozycje zadań do rozwiązania

1. Ile gramów węglanu wapnia rozpuszcza się w 2,5 dm³ wody. Iloczyn rozpuszczalności węglanu wapnia wynosi L = 4,7∙10^-9

2. Ile gramów chlorku ołowiu(II) rozpuszcza się w 250 cm³ wody. Iloczyn rozpuszczalności (L) PbCl₂ wynosi 1,6∙10^-5

3. Rozpuszczalność węglanu kadmu(II) wynosi 3,93 ∙10^-4 g/dm³ Obliczyć wartość iloczynu rozpuszczalności tej soli

4. W 1793 cm³ wody rozpuszcza się dokładnie 1 gram jodku ołowiu(II). Oblicz wartość iloczynu rozpuszczalności tej soli

5. Czy wytrąci się osad węglanu wapnia jeżeli zmieszano równe objętości0,01 molowych roztworów chlorku wapnia i węglanu sodu. Obliczyć ile gramów jonów wapniowych pozostanie w roztworze nasyconym. Stopień dysocjacji soli wynosi 80% a iloczyn rozpuszczalności węglanu wapnia wynosi L = 4,7∙10^-9

6. Ułożyć jonowe równania reakcji roztwarzania się w kwasie solnym następujących trudno rozpuszczalnych związków: CaCO₃; Mg(OH)₂; FeS; Al(OH)₃; Dlaczego rozpuszczają się w kwasie solnym?

7. Ile gramów siarczanu strontu rozpuści się w 10 dm³ wody. Iloczyn rozpuszczalności siarczanu(VI) strontu wynosi L = 7,6∙10^-7

8. Ile gramów jonów srebra pozostanie w 100 cm³ nasyconego roztworu: AgCl; AgBr; AgI. Odpowiednie wartości iloczynów rozpuszczalności wynoszą L_AgCl = 1,1∙10^-10, L_AgBr=5,2∙10^-14; L_AgI = 8,3∙10^-17

9. Czy wytrąci się osad chlorku ołowiu(II) jeżeli do 150 cm³ 0,01 molowego roztworu azotanu(V) ołowiu(II) dodano 350 cm³ 0,02 molowego roztworu chlorku sodowego. Założyć całkowitą dysocjację soli. Iloczyn rozpuszczalności chlorku ołowiu(II) wynosi L = 1,6∙10^-5

10. Obliczyć wartość iloczynu rozpuszczalności Mg(OH)₂ jeżeli jego rozpuszczalność w temperaturze pokojowej wynosi 1,40∙10^-4 mol/dm³

Rozwiązanie zadań na iloczyn rozpuszczalności

Zad.1

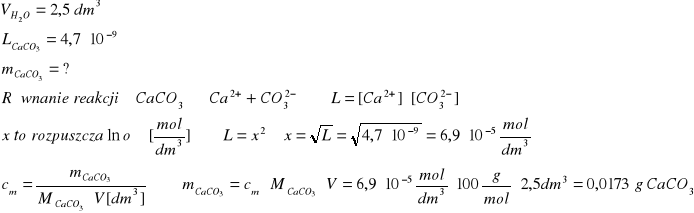
Zad.2

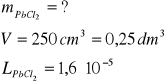
Jeżeli stężenie PbCl₂ = x wówczas [Pb²⁺] = x, zaś [Cl^-] = 2x iloczyn rozpuszczalności L będzie wynosił L = x∙(2x)² = 4x³

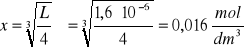
podobnie jak w zadaniu 1 obliczamy masę rozpuszczonej soli PbCl₂

Zad. 3

Rozp. (x) = 3,93∙10^-4 g/dm³

L = ?

Na podstawie podanej rozpuszczalności i masy molowej węglanu kadmu (M = 172 g/mol) obliczymy stężenie molowe (c_m) nasyconego roztworu

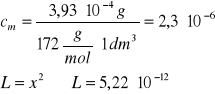
Zad. 4

Z równania reakcji dysocjacji wynika, że jeżeli stężenie jodku ołowiu(II) wynosi x to stężenie [Pb²⁺]= x, zaś stężenie [I^-] = 2x, iloczyn rozpuszczalności PbI₂ wynosi L = x ∙ (2x)² = 4x³ = 4(3,6∙10^-3)³ = 1,9∙10^-7

Zad. 5

po wzajemnym rozcieńczeniu się roztworów w stosunku objętościowym 1 : 1 stężenia jonów wapniowego i węglanowego zmaleją o połowę i będą wynosiły [Ca²⁺] = [CO₃^2-] = 0,005 mol/dm³ iloczyn stężeń tych jonów w roztworze wynosi więc:

0,25 ∙10^-4 i jest większy od iloczynu rozpuszczalności wynoszącego 4,7∙10^-9 Nastąpi więc wytrącenie osadu. Powstaje nasycony roztwór węglanu wapnia, którego iloczyn wynosi L = 4,7∙10^-9 , zaś rozpuszczalność x będzie równa pierwiastkowi z L. Tak więc x = 6,84∙10^-5 mola CaCO₃ , z tego dysocjacji uległo 80%

gdyby dysocjowało w 100% to dysocjowałoby 6,84∙10^-5 mola

80% x moli

Dysocjacji ulega więc 5,47∙10^-5 mola węglanu, dając taką samą ilość moli jonów wapnia czyli 5,47∙10^-5mol∙40g/mol = 2,2∙10^-3g Ca²⁺

Zad. 6

Zapisy cząsteczkowe i jonowe równań reakcji

CaCO₃ + 2HCl = CaCl₂ + H₂O + CO₂(↑)

CO₃^2- + 2H⁺ = H₂O + CO₂

Mg(OH)₂ + 2HCl = MgCl₂ + 2H₂O

OH^- + H⁺ = H₂O

FeS + 2 HCl = H₂S + FeCl₂

S^2- + 2H⁺ = H₂S(↑)

Al(OH)₃ + 3HCl = AlCl₃ + 3H₂O

OH^- + H⁺ = H₂O

Zad.7

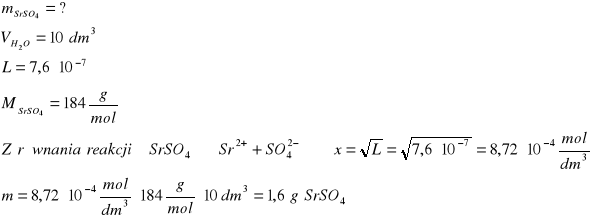
Zad.8

Dla każdej z wymienionych soli z racji analogii wzorów (typ AB)

Kolejno obliczenia dla wymienionych soli srebra

AgCl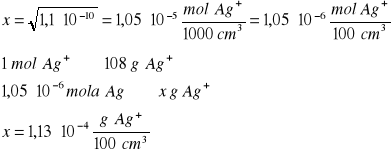

AgBr

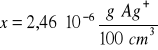
AgI

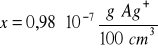
Zad. 9

Obliczamy stężenia jonów po wzajemnym rozcieńczeniu

Pb²⁺ 150 cm³ stężenie 0,01 mol/dm³

500 cm³ stężenie x mol/dm³

[Pb²⁺] = 0,033 mol/dm³

Cl^- 350 cm³ stężenie 0,02 mol/dm³

500 cm³ stężenie y mol/dm³

[Cl^-] = 0,029 mol/dm³

iloczyn stężeń jonów po zmieszaniu roztworów wynosi

L = 0,033 ∙ (0,029)² = 2,69∙10^-5 i ma wartość większą od literaturowej wartości iloczynu rozpuszczalności dla tej soli (1,6∙10^-5) a więc osad się wytrącił.

Zad.10

uwzględniając równanie reakcji dysocjacji Mg(OH)₂↔Mg²⁺+2OH^-

[Mg²⁺] = x zaś [OH^-] = 2x czyli L = x·(2x)²= 4x³

tak więc L = 4·(1,4·10^-4)³ = 1,1·10^-11

1

---